#23 in a series of articles about the technology behind Bang & Olufsen loudspeakers

 

Audio people throw words around like “frequency” and “distortion” and “resolution” and “” without wondering whether anyone else in the room (a) understands or (b) cares. One of the best ways to explain things to people who do not understand but do care is to use analogies and metaphors. So, this week, I’d like to give some visual analogies of common problems in audio.

 

Let’s start with a photograph. Assuming that your computer monitor is identical to mine, and the background light in your room is exactly the same as it is in mine, then you’re seeing what I’m seeing when you look at this photo.

Let’s say that you, sitting there, looking at this photo is analogous to you, sitting there, listening to a recording on a pair of loudspeakers or over headphones. So what happens when something in the signal path messes up the signal?

 

Perhaps, for example, you have a limited range in your system. That could mean that you can’t play the very low and/or high frequencies because you are listening through a smaller set of loudspeakers instead of a full-range model. Limiting the range of brightness levels in the photo is similar to this problem – so nothing is really deep black or bright white. (We could have an argument about whether this is an analogy to a limited dynamic range in an audio system, but I would argue that it isn’t – since audio dynamic range is limited by a noise floor and a clipping level, which we’ll do later…) So, the photo below “sounds” like an audio system with a limited range:

Of course, almost everything is there – sort of – but it doesn’t have the same depth or sparkle as the original photo.

 

 

Or what if you have a noisy device in your signal chain For example, maybe you’re listening to a copy of the recording on a cassette tape – or the air conditioning is on in your listening room. Then the result will “sound” like this:

As you can see, you still have the original recording – but there is an added layer of noise with it. This is not only distracting, but it can obscure some of the more subtle details that are on the same order of magnitude as the noise itself.

 

 

In audio, the quietest music is buried in the noise of the system (either the playback system or the recording system). On the other extreme is the loud music, which can only go so loud before it “clips” – meaning that the peaks get chopped off because the system just can’t go up enough. In other words, the poor little woofer wants to move out of the loudspeaker by 10 mm, but it can only move 4 mm because the rubber holding on to it just can’t stretch any further. In a photo, this is the same as turning up the brightness too much, resulting in too many things just turning white because they can’t get brighter (in the old days of film, this was called “blowing out” the photo), as is shown below.

 

This “clipping” of the signal is what many people mean when they say “distorted” – however, distortion is a much broader range of problems then just clipping. To be really pedantic, any time the output of a system is not identical to its input, then the signal is distorted.

 

 

A more common problem that many people face is a modification of the frequency response. In audio, the frequency is (very generally speaking) the musical pitch of the notes you’re hearing. Low notes are low frequencies, high notes are high frequencies. Large engines emit low frequencies, tiny bells emit high frequencies. With light, the frequency of the light wavicle hitting your eyeball determines the colour that you see. Red is a low frequency and violet is a high frequency (see the table on this page for details). So, if you have a pair of headphones that, say, emphasises bass (the low frequencies) more than the other areas, then it’s the same as making the photo more red, as shown below.

 

 

 

Of course, not all impairments to the audio signal are accidental. Some are the fault of the user who makes a conscious decision to be more concerned with convenience (i.e. how many songs you can fit on your portable player) than audio quality. When you choose to convert your CD’s to a “lossy” format (like MP3, for example), then (as suggested by the description) you’re losing something. In theory, you are losing things that aren’t important (in other words, your computer thinks that you can’t hear what’s thrown away, so you won’t miss it). However, in practice, that debate is up to you and your computer (and your bitrate, and the codec you’ve chosen, and the quality of the rest of your system, and how you listen to music, and what kind of music you’re listening to, and whether or not there are other things to listen to at the same time, and a bunch of other things…) However, if we’re going to make an analogy, then we have to throw away the details in our photo, keeping enough information to be moderately recognisable.

As you can see, all the colours are still there. And, if you stand far enough away (or if you take off your glasses) it might just look the same. But, if you look carefully enough, then you might notice that something is missing… Keep looking… you’ll see it…

 

 

So, as you can see, any impairment of the “signal” is a disruption of its quality – but we should be careful not to confuse this with reality. There are lots of people out there who have a kind of weird religious belief that, when you sit and listen to a recording of an orchestra, you should be magically transported to a concert hall as if you were there (or as if the orchestra were sitting in your listening room). This is silly. That’s like saying when you sit and watch a re-run of Friends on your television, you should feel like you’re actually in the apartment in New York with a bunch of beautiful people. Or, when you watch a movie, you feel like you’re actually in a car chase or a laser battle in space. Music recordings are no more of a “virtual reality” experience than a television show or a film. In all of these cases (the music recording, the TV episode and the film), what you’re hearing and seeing should not be life-like – they should be better than life. You never have to wait for the people in a film to look for a parking space or go out to pee. Similarly, you never hear a mistake in the trumpet solo in a recording of  Berlin Philharmonic and you always hear Justin Bieber singing in tune. Even the spatial aspects of an “audiophile” classical recording are better-than-reality. If you sit in a concert hall, you can either be close (and hear the musicians much louder than the reverberation) or far (and hear much more of the reverberation). In a recording, you are sitting both near and far – so you have the presence of the musicians and the spaciousness of the reverb at the same time. Better than real life!

So, what you’re listening to is a story. A recording engineer attended a music performance, and that person is now recounting the story of what happened in his or her own style. If it’s a good recording engineer, then the storytelling is better than being there – it’s more than just a “police report” of a series of events.

To illustrate my point, below is a photo of what that sinking WWII bunker actually looked like when I took the photo that I’ve been messing with.

 

Of course, you can argue that this is a “better” photo than the one at the top – that’s a matter of your taste versus mine. Maybe you prefer the sound of an orchestra done recorded with only two microphones played through two loudspeakers. Maybe you prefer the sound of the same orchestra recorded with lots of microphones played through a surround system. Maybe you like listening to singers who can sing. Maybe you like listening to singers who need auto tuners to clean up the mess. This is just personal taste. But at least you should be choosing to hear (or see) what the artist intended – not a modified version of it.

This means that the goal of a sound system is to deliver, in your listening room, the same sound as the recording engineer heard in the studio when he or she did the recording. Just like the photos you are looking at on the top of this page should look exactly the same as what I see when I see the same photo.

 

 

 

 

#21 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Part 1: Equal Loudness Contours

Let’s start with some depressing news: You can’t trust your ears. Sorry, but none of us can.

There are lots of reasons for this, and the statement is actually far more wide-reaching than any of us would like to admit. However, in this article, we’re going to look at one small aspect of the statement, and what we might be able to do to get around the problem.

We’ll begin with a thought experiment (although, for some of you, this may be an experiment that you have actually done). Imagine that you go into the quietest room that you’ve ever been in, and you are given a button to press and a pair of headphones to put on. Then you sit and wait for a while until you calm down and your ears settle in to the silence… While that’s happening you read the instructions of the task with which you are presented:

Whenever you hear a tone in the headphones in either one of your ears, please press the button.

Simple! Hear a beep, press the button. What could be more difficult to do than that?

Then, the test begins: you hear a beep in your left ear and you press the button. You hear another, quieter beep and you press the button again. You hear an even quieter beep and you press the button. You hear nothing, and you don’t press the button. You hear a beep and you press the button. Then you hear a beep at a lower frequency and so on and so on. This goes on and on at different levels, at different frequencies, in your two ears, until someone comes in the room and says “thank you, that will be all”.

While this test seems like it would be pretty easy to do, it’s a little unnerving. This is because the room that you’re sitting in is so quiet and the beeps are also so quiet that, sometimes you think you hear a beep – but you’re not sure, because things like the sound of your heartbeat, and your breathing, and the “swooshing” of blood in your body, and that faint ringing in your ears, and the noise you made by shifting in your chair are all, relatively speaking VERY loud compared to the beeps that you’re trying to detect.

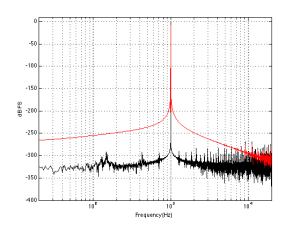
Anyways, when you’re done, you’ll might be presented with a graph that shows something called your “threshold of hearing”. This is a map of how loud a particular frequency has to be in order for you to hear it. The first thing that you’ll notice is that you are less sensitive to some frequencies than others. Specifically, a very low frequency or a very high frequency has to be much louder for you to hear it than if you’re listening to a mid-range frequency. (There are evolutionary reasons for this that we’ll discuss at the end.) Take a look at the bottom curve on Figure 1, below:

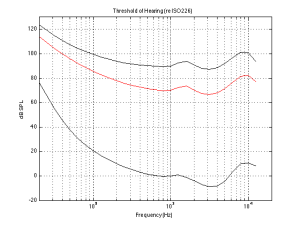
The bottom curve on this plot shows a typical result for a threshold of hearing test for a person with average hearing and no serious impairments or temporary issues (like wax build-up in the ear canal).  What you can see there is that, for a 1 kHz tone, your threshold of hearing is 0 dB SPL (in fact, this is how 0 dB SPL is defined…) As you go lower in frequency from there, you will have to turn up the actual signal level just in order for you to hear it. So, for example, you would need to have approximately 60 dB SPL at 30 Hz in order to be able to detect that something is coming out of your headphones or loudspeakers. Similarly, you would need something like 10 dB SPL at 10 kHz in order to hear it. However, at 3.5 kHz, you can hear tones that are quieter than 0 dB SPL! It stands to reason, then, that a 30 Hz tone at 60 dB SPL and a 1 kHz tone at 0 dB SPL and a 3.5 kHz tone at about -10 dB SPL and a 10 kHz tone at about 10 dB SPL would all appear to have the same loudness level (since they are all just audible).

Let’s now re-do the test, but we’ll change the instructions slightly. I’ll give you a volume knob instead of a button and I’ll play two tones at different frequencies. The volume knob only changes the level of one of the two tones, and your task is to make the two tones the same apparent level. If you do this over and over for different frequencies, and you plot the results, you might wind up with something like the red or the top curves in Fig 1. These are called “Equal Loudness Contours” (some people call them “Fletcher-Munson Curves because the first two researchers to talk about them were Fletcher and Munson) because they show how loud different frequencies have to be in order for you to think that they have the same loudness. So, (looking at the red curve) a 40 Hz tone at 100 dB SPL sounds like it’s the same loudness as a 1 kHz tone at 70 dB SPL or a 7.5 kHz tone at 80 dB SPL. The loudness level that you think you’re hearing is measured in “phons” – and the phon value of the curve is its value in dB SPL at 1 kHz. For example, the red curve crosses the 1 kHz line at 70 dB SPL, so it’s   the “70 phon” curve. Any tone that has an actual level in dB SPL that corresponds to a point on that red line will have an apparent loudness of 70 phons. The top curve is for the 90 phons.

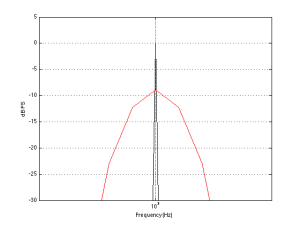
Figure 2 shows the Equal Loudness Contours from 0 phons (the Threshold of Hearing) to 90 phons in steps of 10 phons.

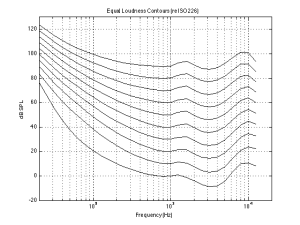
There are two important things to notice about these curves. The first is that they are not “flat”. In other words, your ears do not have a flat frequency response. In fact, if you were measured the same way we measure microphones or loudspeakers, you’d have a frequency response specification that looked something like “20 Hz – 15 kHz ±30 dB” or so… This isn’t something to worry about, because we all have the same problem. So, this means that the orchestra conductor asked the bass section to play louder because he’s bad at hearing low frequencies, and the recording engineer balancing the recording adjusted the bass-to-midrange-to-treble relative levels using his bad hearing, and, assuming that the recording system and your playback system are reasonably flat-ish, then hopefully, your hearing is identically bad to the conductor and recording engineer, so you hear what they want you to.

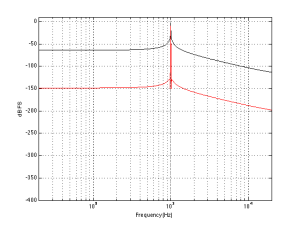
However, I said that there are two things to notice – that was just the first thing. The second thing is that the curves are different at different levels. For example, if you look at the 0 phon curve (the bottom one) you’ll see that it raises a lot more in the low frequency region than, say, the 90 phon curve (the top one) relative to their mid-range values. This means that, the quieter the signal, the worse your ability to hear bass (and treble). For example, let’s take the curves and assume that the 70 phon line is our reference – so we’ll make that one flat, and adjust all of the others accordingly and plot them so we can see their difference. That’s shown in Figure 3.

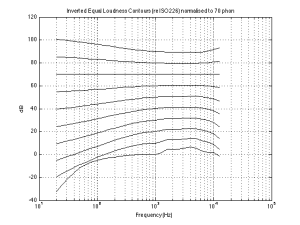
What does Figure 3 show us, exactly? Well, one way to think of it is to go back to our “recording engineer vs. you” example. Let’s say that the recording engineer that did the recording set the volume knob in the recording studio so that (s)he was hearing the orchestra with a loudness at the 70 phon line. On other words, if the orchestra was playing a 1 kHz sine tone, then the level of the signal was 70 dB SPL at the listening position – and all other frequencies were balanced by the conductor and the engineer to appear to sound the same level as that. Then you take the recording home and set the volume so that you’re hearing things at the 30 phon level (because you’re having a dinner party and you want to hear the conversation more than you want to hear Beethoven or Justin Bieber, depending on your taste or lack thereof). Look at the curve that intersects the -40 dB line at 1 kHz (the 4th one from the bottom) in Figure 3. This shows you your sensitivity difference relative to the recording engineer’s in this example. The curve slopes downwards – meaning that you can’t hear bass as well – so, your recording playing in the background will appear to have a lot less bass and a little less treble than what the recording engineer heard – just because you turned down the volume. (Of course, this may be a good thing, since you’re having dinner and you probably don’t want to be distracted from the conversation by thumpy bass and sparkly high frequencies.)

Part 2: Compensation

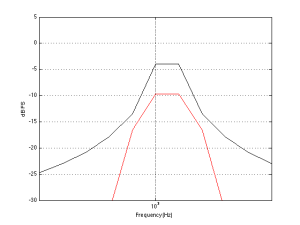
In order to counter-act this “misbehaviour” in your hearing, we have to change the balance of the frequency bands in the opposite direction to what your ears are doing. So if we just take the curves in Figure 3 and flip each of them upside down, you have a “perfect” correction curve showing that, when you turn down the volume by, say 40 dB (hint: look at the value at 1 kHz) then you’ll need to turn up the low end by lots to compensate and make the overall balance sound the same.

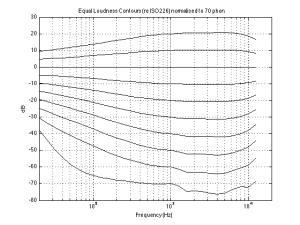
Of course, these curves shown in Figure 4 are normalised to one specific curve – in this case, the 70 phon curve. So, if your recording engineer was monitoring at another level (say, 80 phons) then your “perfect” correction curves will be wrong.

And, since there’s no telling (at least with music recordings) what level the recording and mastering engineers used to make the recording that you’re listening to right now (or the one you’ll hear after this one), then there’s no way of predicting what curve you should use to  do the correction for your volume setting.

All we can really say is that, generally, if you turn down the volume, you’ll have to turn up the bass and treble to compensate. The more you turn down the volume, the more you’ll have to compensate. However, the EXACT amount by which you should compensate is unknown, since you don’t know anything about the playback (or monitoring) levels when the recording was done. (This isn’t the same for movies, since re-recording engineers are supposed to work at a fixed monitoring level which should be the same as all the cinemas in the world… in theory…)

This compensation is called “loudness” – although in some cases it would be better termed “auto-loudness”. In the old days, a “loudness” switch was one that, when engaged, increased the bass and treble levels for quiet listening. (Of course, what most people did was hit the “loudness”switch and left it on forever.) Nowadays, however, this is usually automatically applied and has different amounts of boost for different volume settings (hence the “auto-” in “auto-loudness”). For example, if you look at Figure 5 you’ll see the various amounts of boost applied to the signal at different volume settings of the BeoPlay V1 / BeoVision 11 / BeoSystem 4 / BeoVision Avant when the default settings have not been changed. The lower the volume setting, the higher the boost.

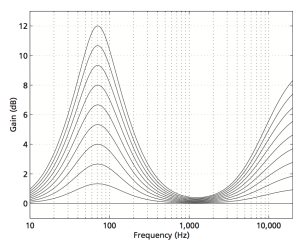
Of course, in a perfect world, the system would know exactly what the monitoring levels was when they did the recording, and the auto-loudness equalisation would change dynamically from recording to recording. However, until there is meta-data included in the recording itself that can tell the system information like that, then there will be no way of knowing how much to add (or subtract).

Historical Note

I mentioned above that the extra sensitivity we have in the 3 kHz region is there due to evolution. In fact, it’s a natural boost applied to the signal hitting your eardrum as a result of the resonance of the ear canal. We have this boost (I guess, more accurately, we have this ear canal) because, if you snap a twig or step on some dry leaves, the noise that you hear is roughly in that frequency region. So, once-upon-a-time, when our ancestors were something else’s lunch, the ones with the ear canals and the resulting mid-frequency boost were more sensitive to the noise of a sabre-toothed tiger trying to sneak up behind them, stepping on a leaf, and had a little extra head start when they were running away. (It’s like the T-shirt that you can buy when you’re visiting Banff, Alberta says: “I don’t need to run faster than the bear. I just need to run faster than you.”)

As an interesting side note to this: the end result of this is that our language has evolved to use this sensitive area. The consonants in our speech – the “s” and”t” sounds, for example, sit right in that sensitive region to make ourselves easiest to understand.

Warning note

You might come across some youtube video or a downloadable file that let’s you “check your hearing” using a swept sine wave. Don’t bother wasting your time with this. Unless the headphones that you’re using (and everything else in the playback chain) are VERY carefully calibrated, then you can’t trust anything about such a demonstration. So don’t bother.

Warning note #2 – Post script…

I just saw on another website here that someone named John Duncan made the following comment about what I wrote in this article. “Having read it a couple of times now, tbh it feels like it is saying something important, I’m just not quite sure what. Is it that a reference volume is the most important thing in assessing hifi?” The answer to this is “Exactly!” If you compare two sound systems (say, two different loudspeakers, or two different DAC’s or two different amplifiers and so on… The moral of the stuff I talk about above is that, not only in such a comparison do you have to make sure that you only change one thing in the system (for example, don’t compare two DAC’s using a different pair of loudspeakers connected to each one) you absolutely must ensure that the two things you’re comparing are EXACTLY the same listening level. A different of 1 dB will have an effect on your “frequency response” and make the two things sound like they have different timbral balances – even when they don’t.

For example, when I’m tuning a new loudspeaker at work, I always work at the same fixed listening level. (for me, this is two channels of -20 dB FS full-band uncorrelated pink noise produces 70 dB SPL, C-weighted at the listening position). Before I start tuning, I set the level to match this so that I don’t get deceived by my own ears. If I tuned loudspeakers quieter than this, I would push up the bass to compensate. If I tuned louder, then I would reduce the bass. This gives me some consistency in my work. Of course, I check to see how the loudspeakers sound at other listening levels, but, when I’m tuning, it’s always at the same level.