A Foundation for Electronic Music

I found this document from Roland, published in 1978. The information in here is still valuable – and presented as an excellent introduction.

Distortion effects on Linear measurements, Part 4

In Part 3, I showed that a magnitude responses calculated from impulse responses produced by the MLS and swept sine methods produce different results when the measurement signals themselves are distorted.

In this posting, I’ll focus on the swept sine method which showed that the apparent magnitude response of the system looked like a strange version of a low shelving filter, but there’s a really easy explanation for this that goes back to something I wrote in Part 1.

The way these systems work is to cross-correlate the signal that comes back from the DUT with the signal that was sent to it. Cross-correlation (in this case) is a bit of math that tells you how similar two signals are when they’re compared over a change in time (sort of…). So, if the incoming signal is identical to the outgoing signal at one moment in time but no other, then the result (the impulse response) looks like a spike that hits 1 (meaning “identical”) at one moment, and is 0 (meaning “not at all alike in any way…”) at all other times.

However, one important thing to remember is that both an MLS signal and a swept sine wave take some time to play. So, on the one hand, it’s a little weird to think of a 10-second sweep or MLS signal being converted to a theoretically-infinitely short impulse. On the other hand, this can be done if the system doesn’t change in time and therefore never changes: something we call a Linear Time-Invariant (or LTI) system.

But what happens if the DUT’s behaviour DOES change over time? Then things get weird.

At the end of Part 1, I said

For both the MLS and the sine sweep, I’m applying a pre-emphasis filter to the signal sent to the DUT and a reciprocal de-emphasis filter to the signal coming from it. This puts a bass-heavy tilt on the signal to be more like the spectrum of music. However, it’s not a “pinking” filter, which would cause a loss of SNR due to the frequency-domain slope starting at too low a frequency.

Then, in Part 2 I said that, to distort the signals, I

look for the peak value of the measurement signal coming into the DUT, and then clip it.

It’s the combination of these two things that results in the magnitude response of the system measured using a swept sine wave looking the way it does.

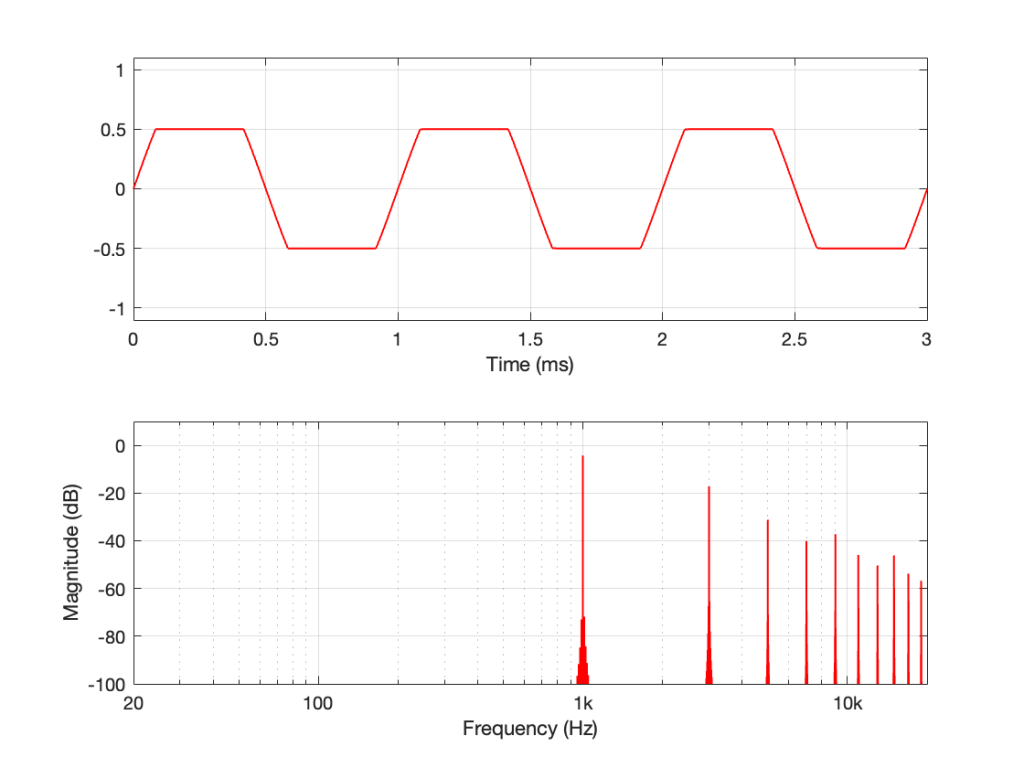
If I look at the signal that I actually send to the input of the DUT, it looks like this:

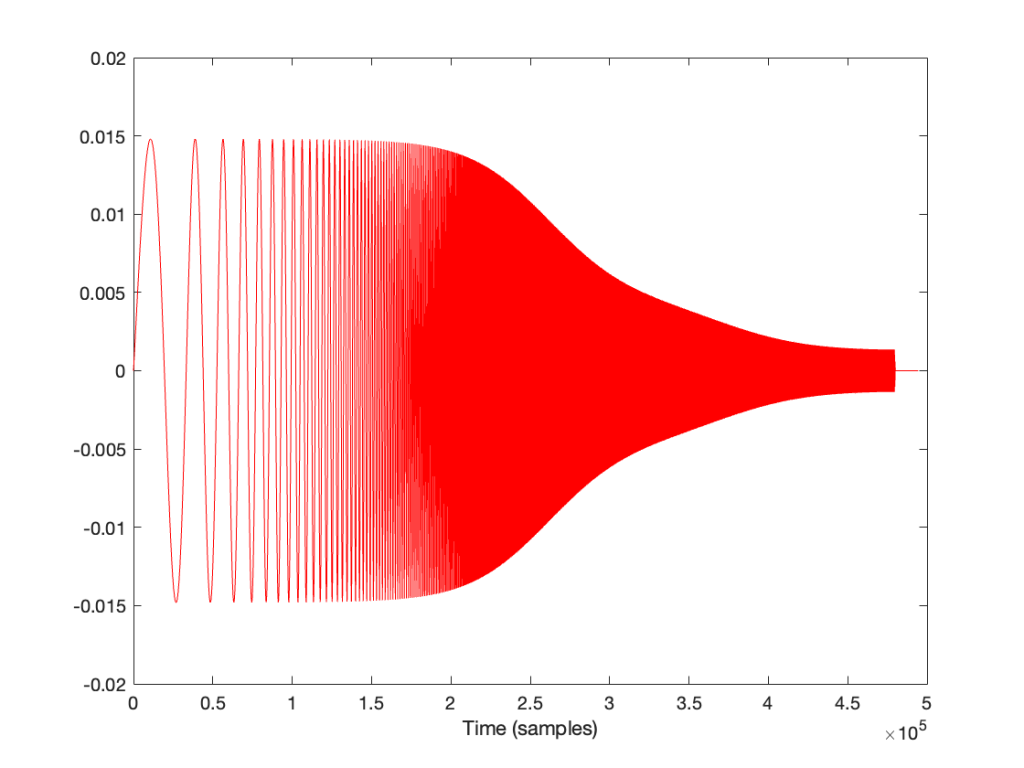
I’m normalising this to have a maximum value of 1 and then clipping it at some value like ±0.5, for example, like this:

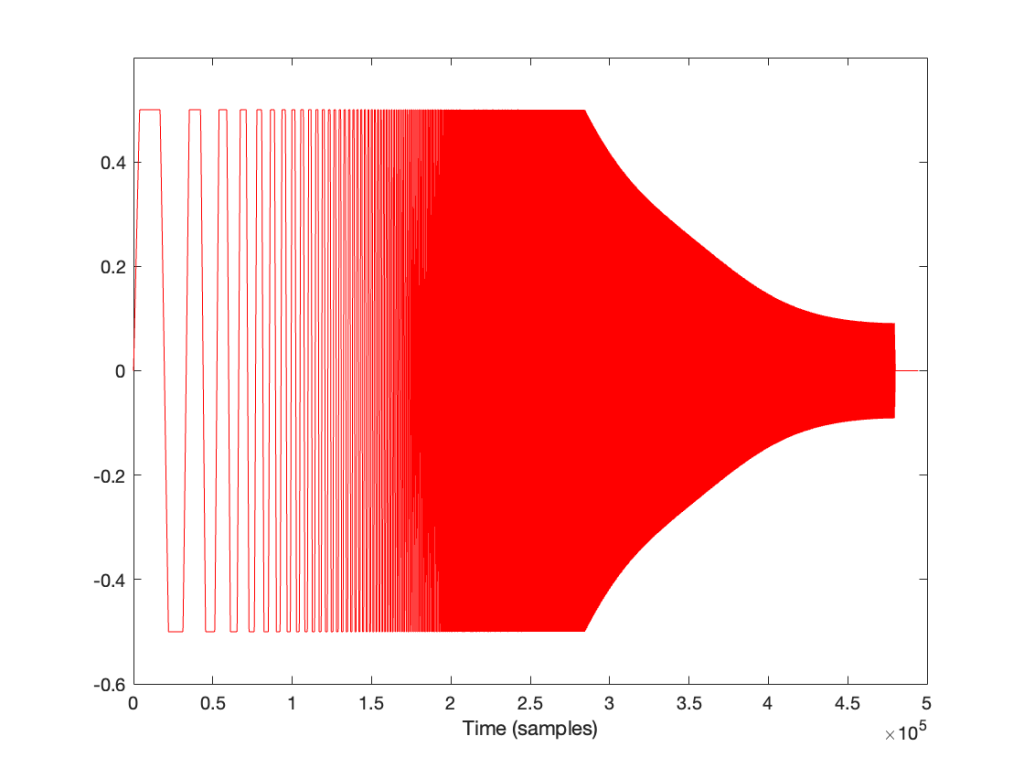
So, it should be immediately obvious that, by choosing to clip the signal at 1/2 of the maximum value of the whole sweep, I’m not clipping the entire thing. I’m only distorting signals below some frequency that is related to the level at which I’m clipping. The harder I clip, the higher the frequency I mess up.

This is why, when we look at the magnitude response, it looks like this:

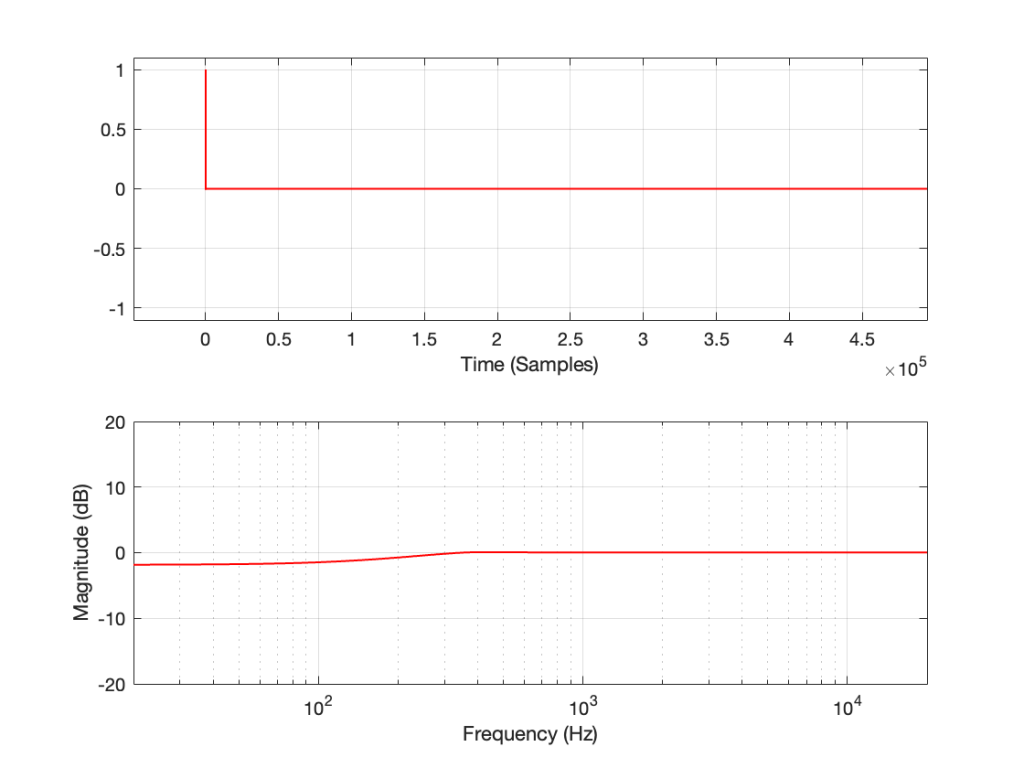
In the very low frequencies, the magnitude response is flat, but lower than expected, because the signal is clipped by the same amount. In the high frequencies, the signal is not clipped at all, so everything is behaving. In between these two bands, there is a transition between “not-behaving” and “behaving”.

This means that

if the signal I was sending into the system was clipped by the same amount at all frequencies, OR
if the pre-emphasis wasn’t applied to the signal, boosting the low frequencies

Then the magnitude response would look almost flat, but lower than expected (by the amount that is related to how much it’s clipped). In other words, we would (mostly) see the linear response of the system, even though it was behaving non-linearly – almost like if we had only sent a click through it.

However, if we chose to not apply the pre-emphasis to the signal, then the DUT wouldn’t be behaving the way it normally does, since this is very roughly equivalent to the spectral balance of music. For example, if you send a swept sine wave from 20 Hz to 20,000 Hz to a loudspeaker without applying that bass boost, you’ll could either get almost nothing out of your woofer, or you’ll burn out your tweeter (depending on how loudly you’re playing the sweep).

How does the result look without the pre-emphasis filter applied to the swept sine wave? For example, if we sent this to the DUT:

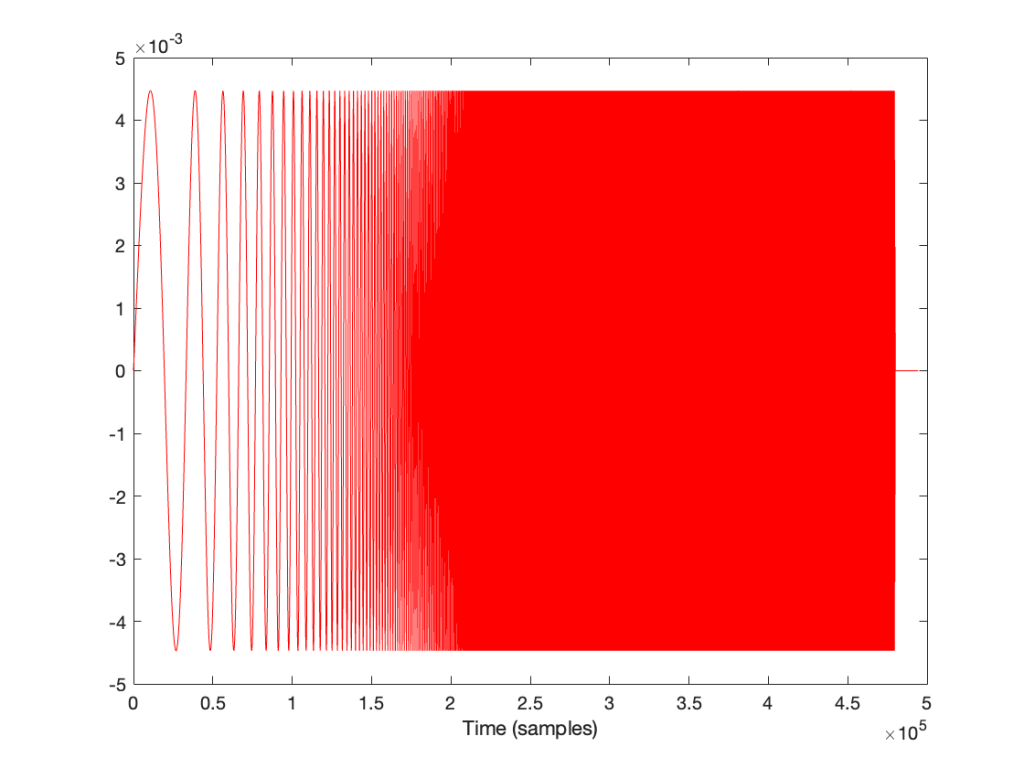
… and then we clipped it at 1/2 the maximum value, so it looks like this:

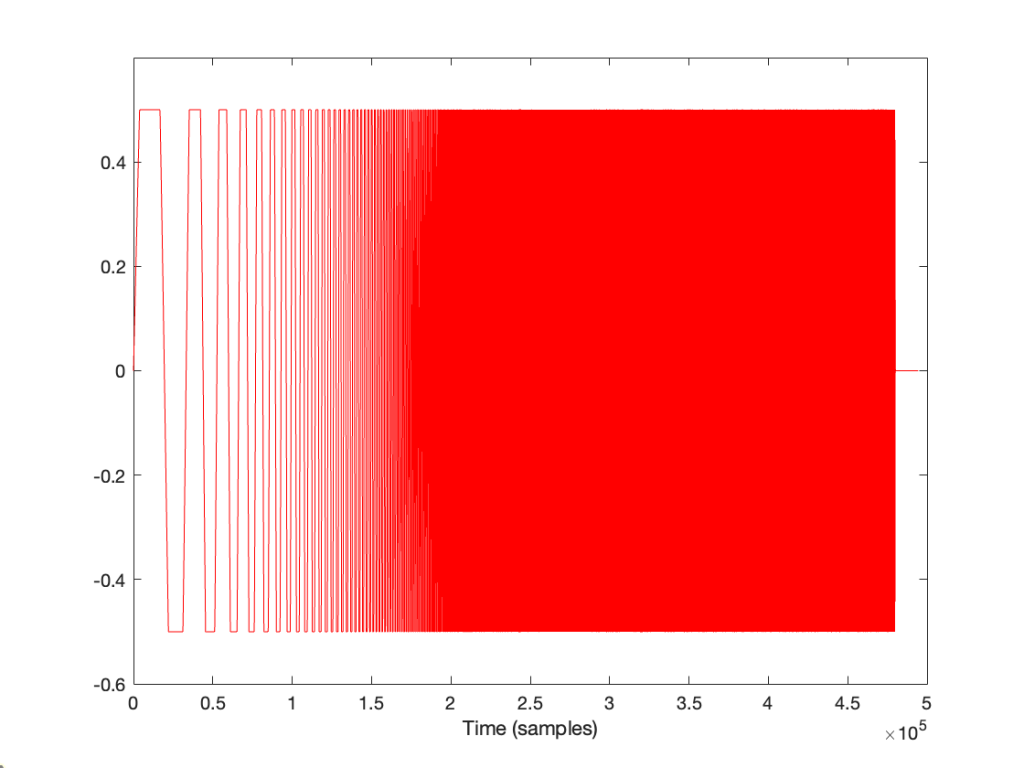
(notice that everything is clipped)

then the impulse response and magnitude response look like this instead:

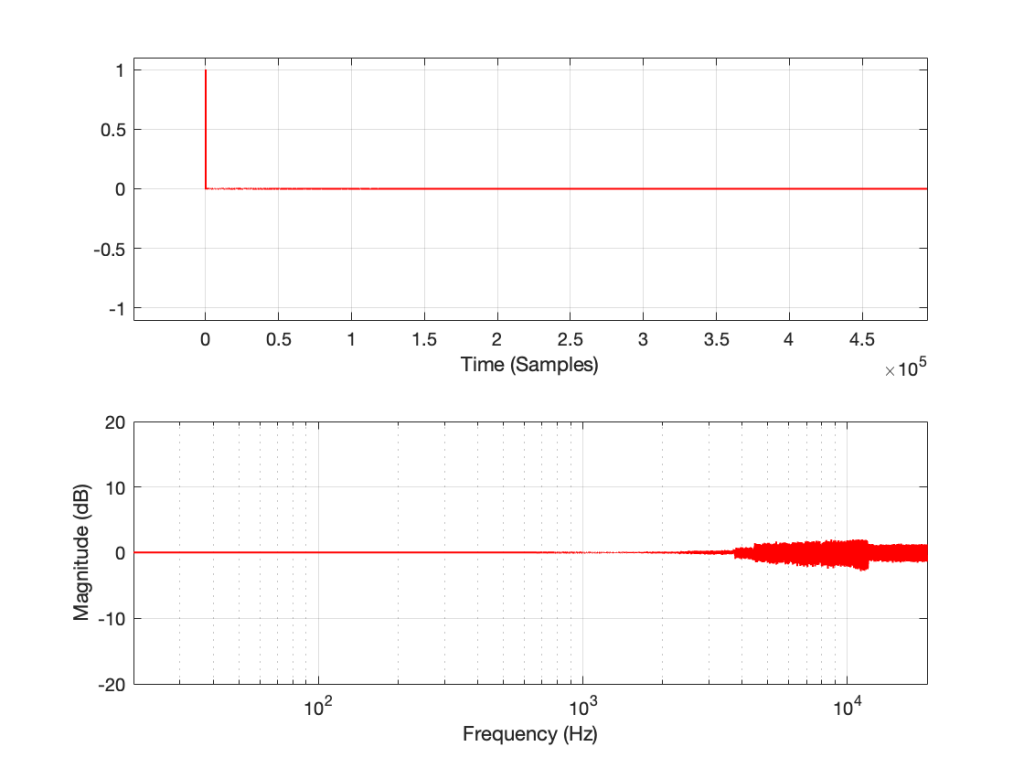
… which is more similar to the results when we clip the MLS measurement signal in that we see the effects on the top end of the signal. However, it’s still not a real representation of how the DUT “sounds” whatever that means…

Distortion effects on Linear measurements, Part 3

This posting will just be some more examples of the artefacts caused by symmetrical clipping of the measurement signal for the MLS and swept-sine methods, clipping at different levels.

Remember that the clip level is relative to the peak level of the measurement signal.

MLS

Swept Sine

Swept Sine, clipping at 0.5 of peak level

Swept Sine, clipping at 0.3 of peak level

Swept Sine, clipping at 0.1 of peak level

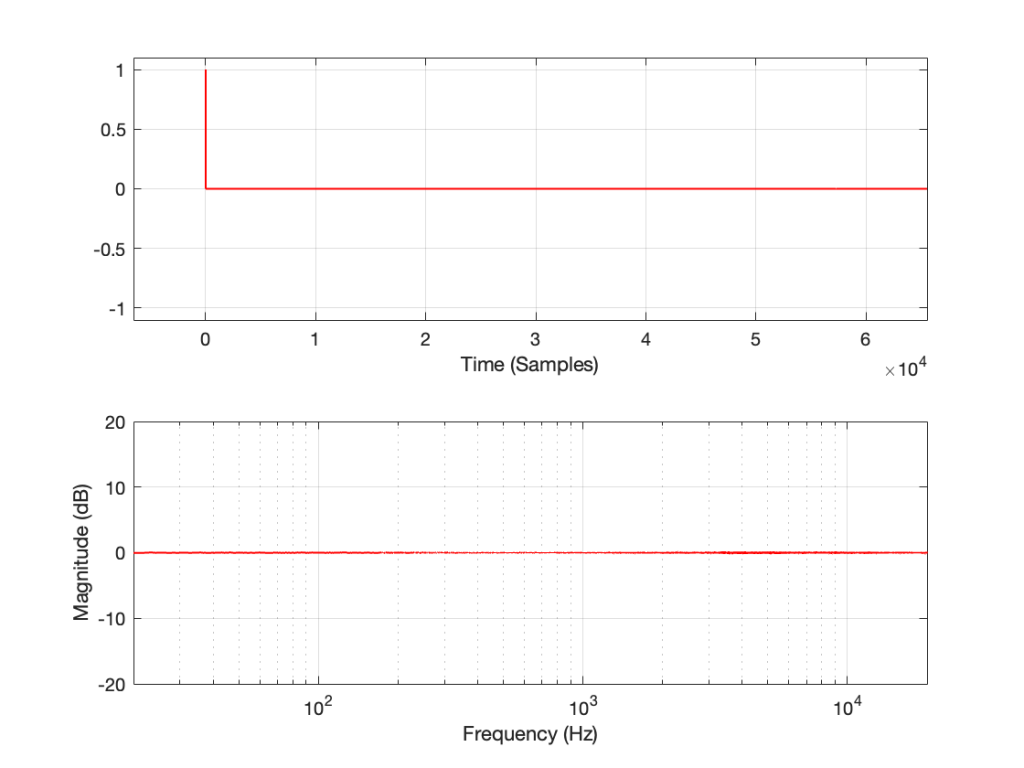
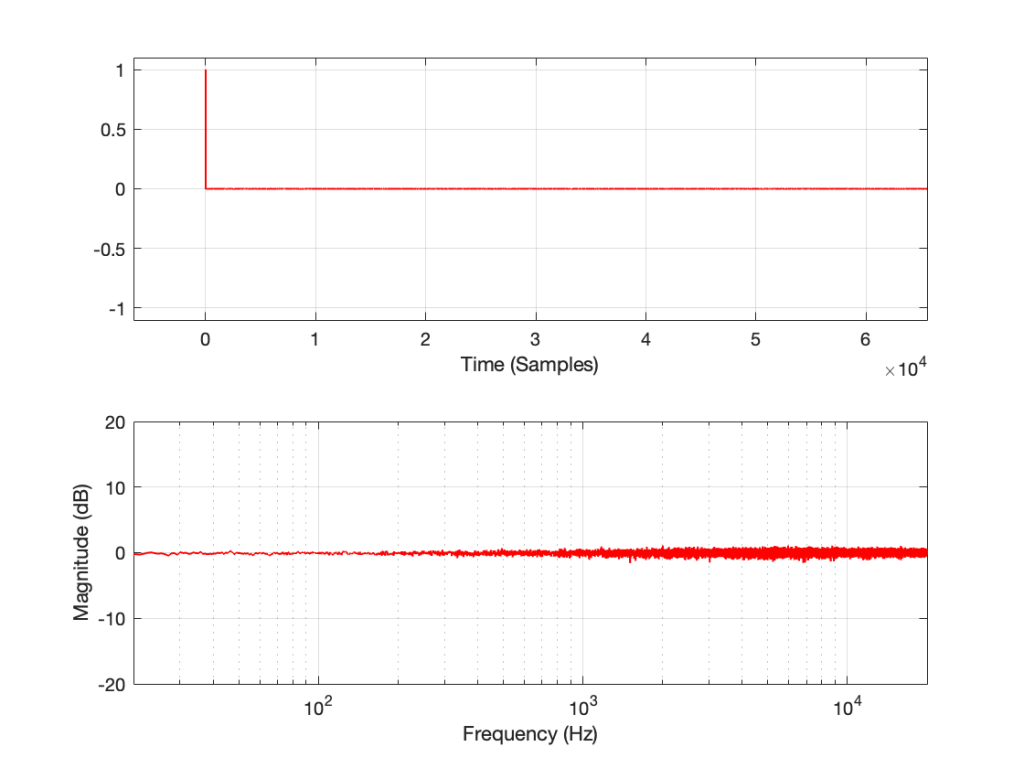
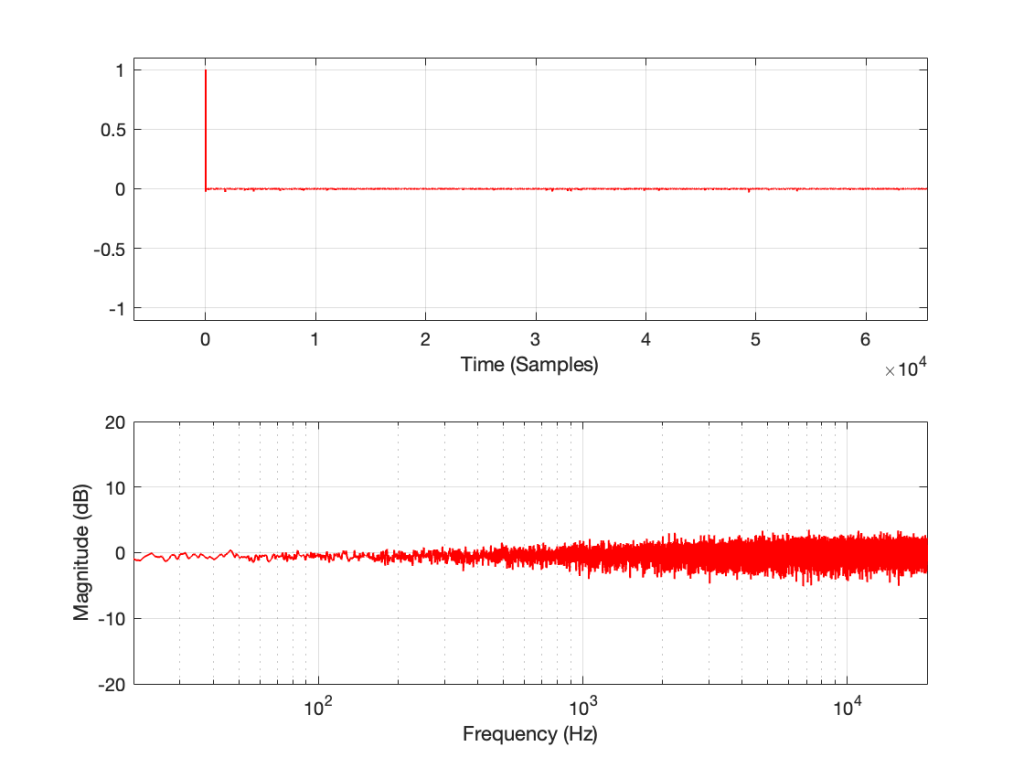
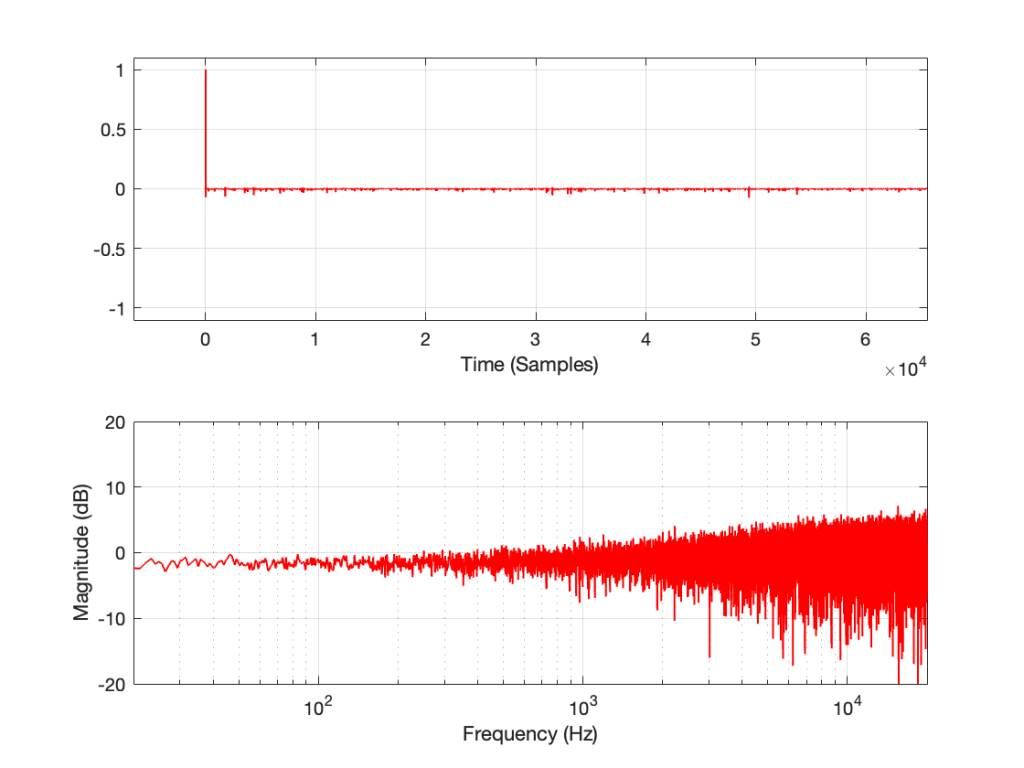
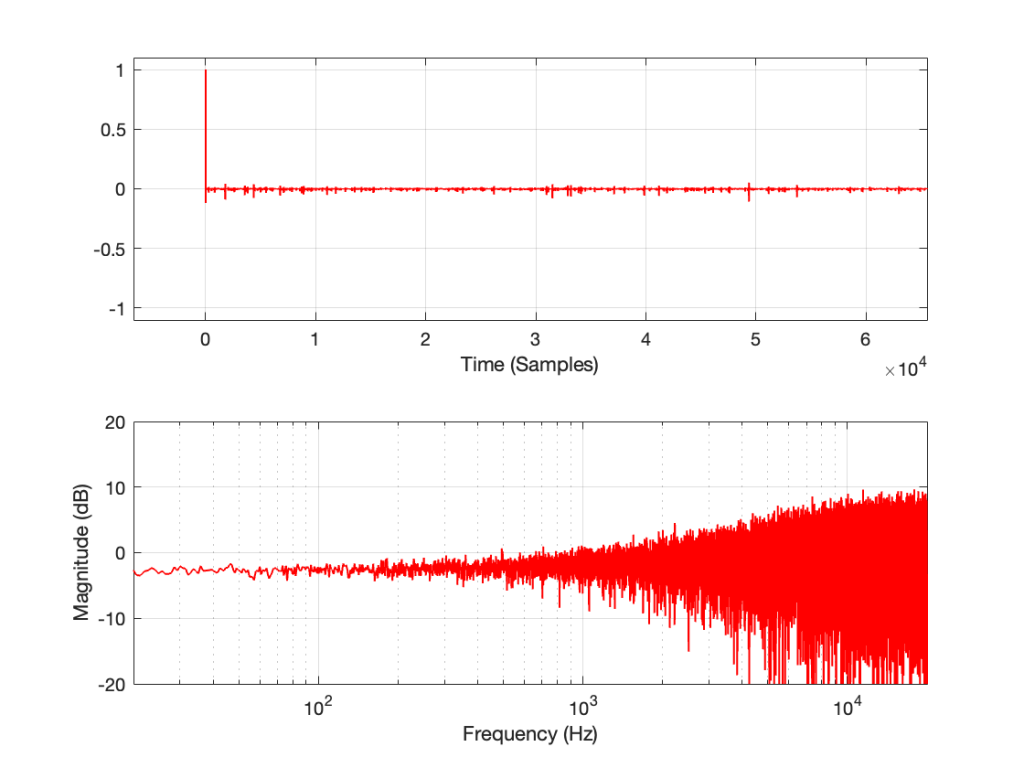
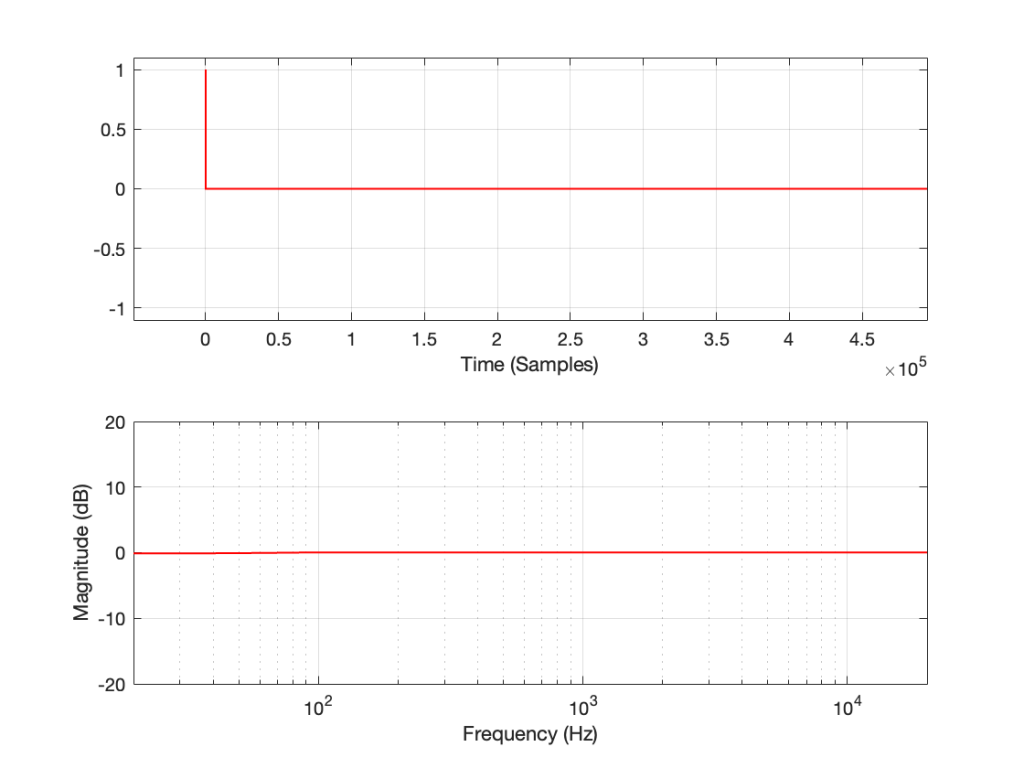
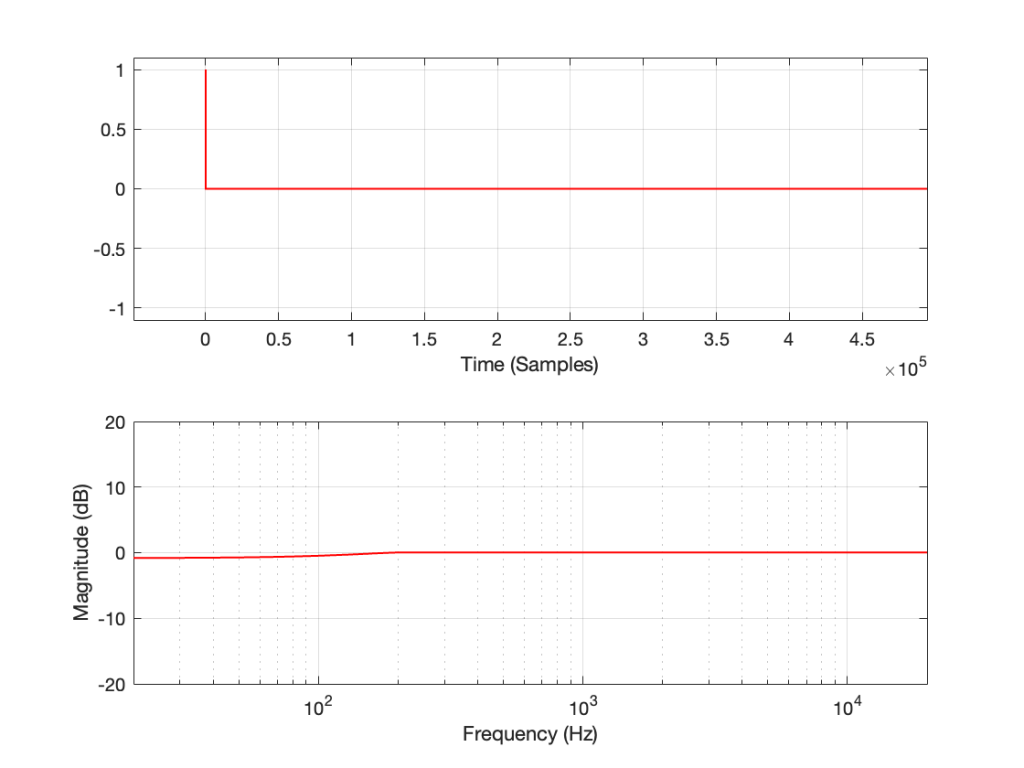
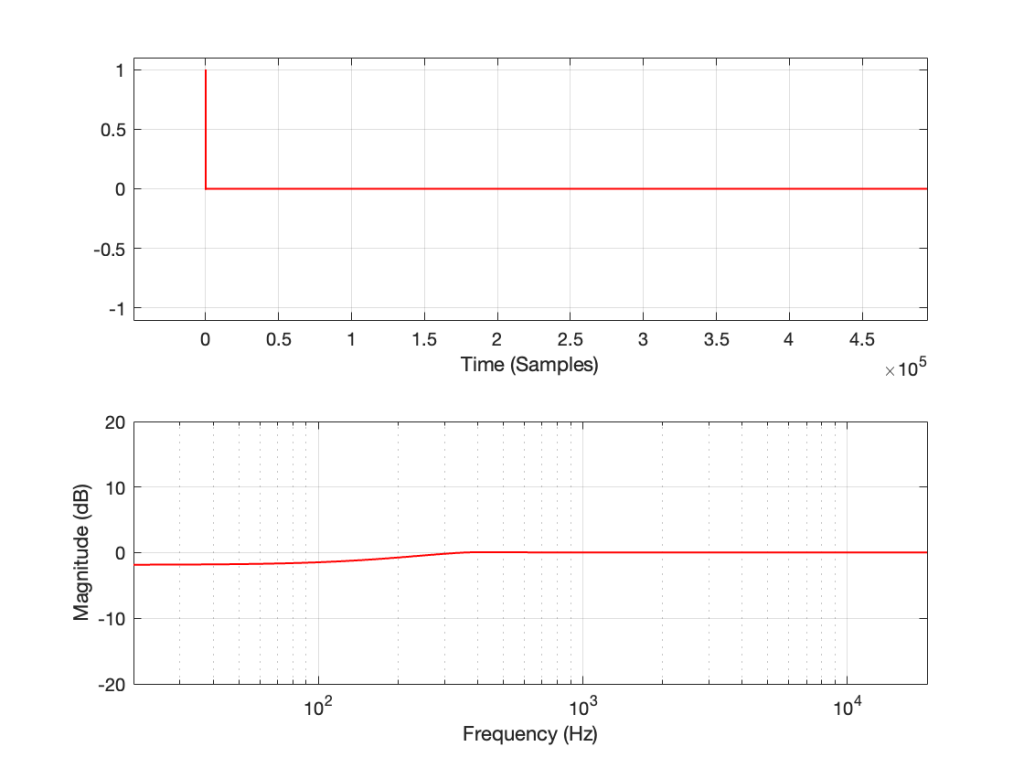
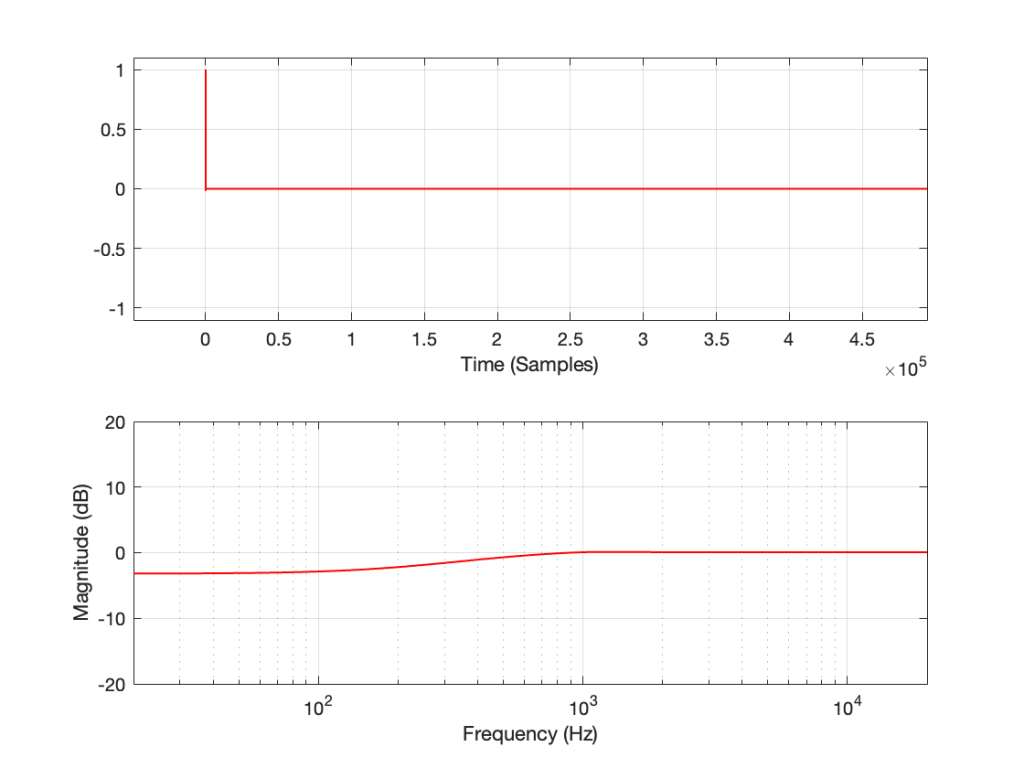
The take-home message here is that, although both the MLS and the swept sine methods suffer from showing you strange things when the DUT is clipping, the swept sine method is much less cranky…

In the next posting, I’ll explain why this is the case.

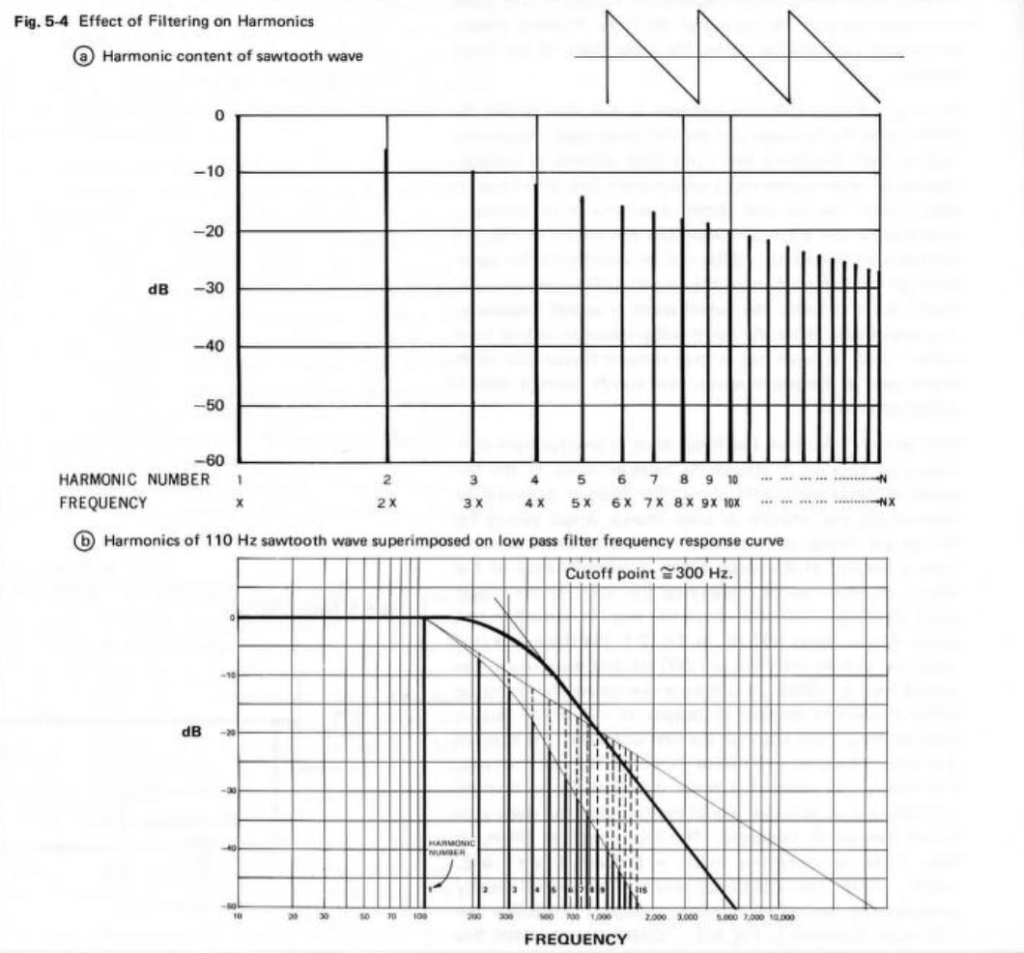
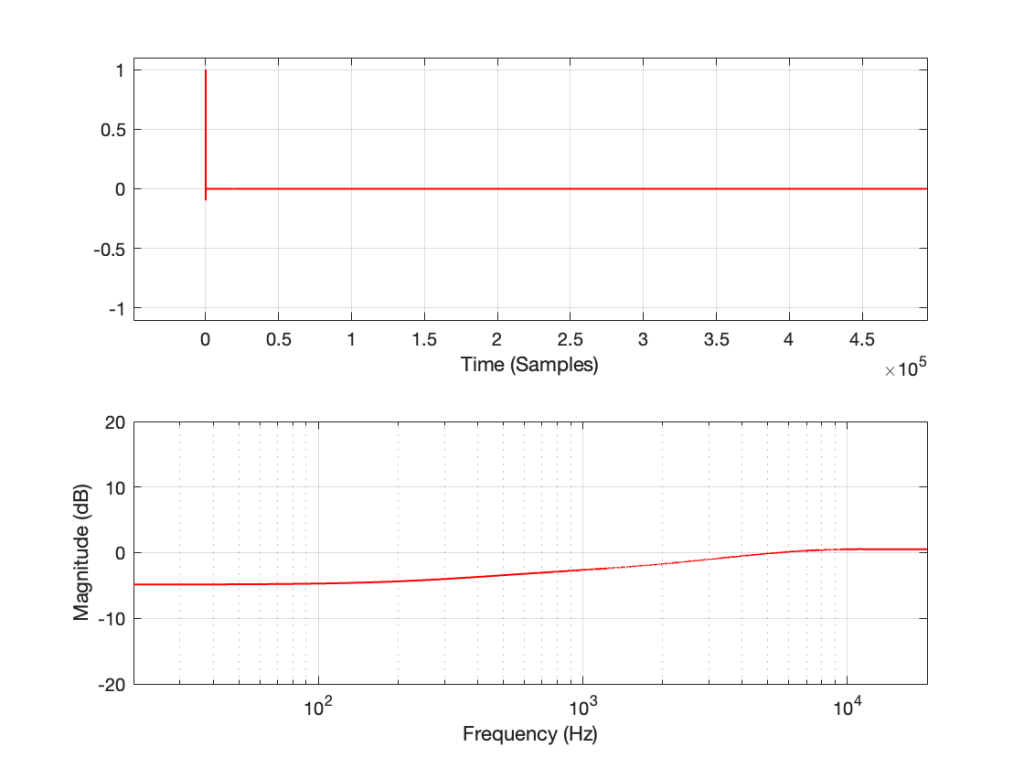
Distortion effects on Linear measurements, Part 2

Let’s make a DUT with a simple distortion problem: It clips the signal symmetrically at 0.5 of the peak value of the signal, so if I send in a sine wave at 1 kHz, it looks like this:

Figure 1: An example of a symmetrically-clipped sine wave with a fundamental frequency of 1 kHz.

Now, to be fair, what I’m REALLY doing here is to look for the peak value of the measurement signal coming into the DUT, and then clipping it. This would be equivalent to doing a measurement of the DUT and adjusting the input gain so that it looks like a peak level of – 6 dB relative to maximum is coming in.

Also, because what I’m about to do through this series is going to have radical effects on the level after processing, I’m normalising the levels. So, some things won’t look right from a perspective of how-loud-it-appears-to-be.

If I measure that DUT using the three methods, the results look like this:

Figure 2: The impulse response of a clipping DUT, measured with an impulse (plot has been normalised for level).

Figure 3: The impulse response of a clipping DUT, measured with an MLS sequence (plot has been normalised for level).

Figure 4: The impulse response of a clipping DUT, measured with a swept sine (plot has been normalised for level).

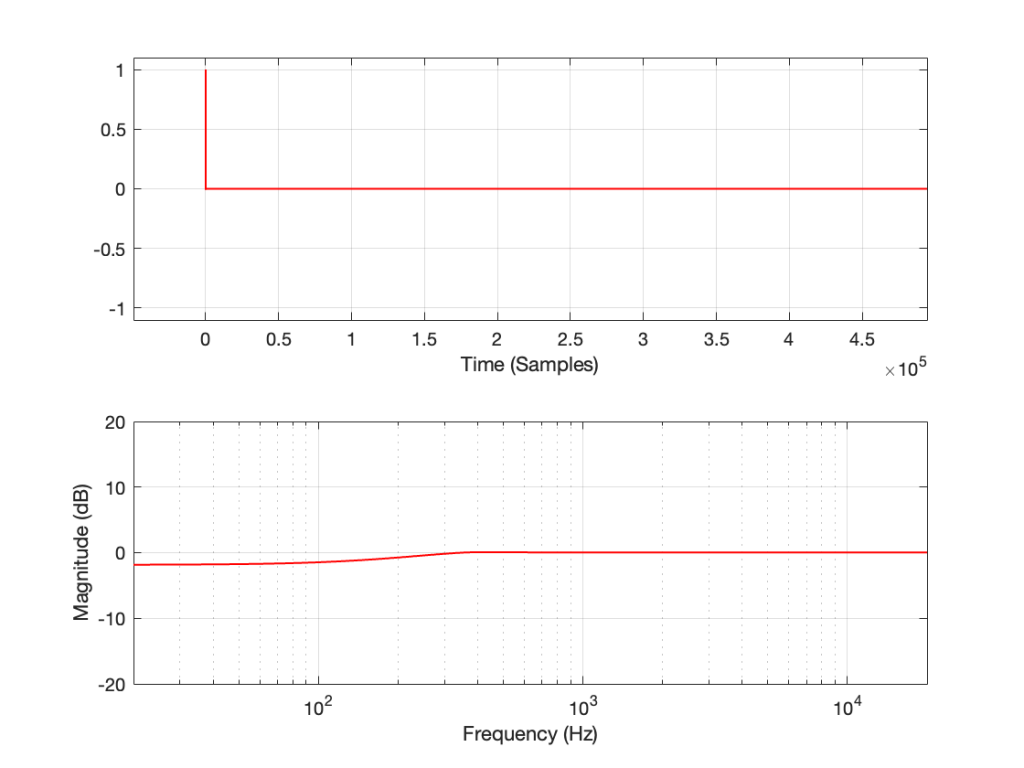
As can easily be seen above, the three systems show very different responses. So, unlike what I claimed this post (which is admittedly over-simplified, although intentionally so to make a point…), the fact that they are measuring the impulse response does not mean that we can’t see the effects of the non-linear response. We can obviously see artefacts in the linear response that are caused by the distortion, but those artefacts don’t look like distortion, and they don’t really show us the real linear response.

Distortion effects on Linear measurements, Part 1

In the last posting, I made a big assumption: that it’s normal to measure the magnitude response of a device via an impulse response measurement.

In order to illustrate the fact that an impulse response measurement shows you only the linear response of a system (and not distortion effects such as clipping), I did an impulse response measurement using an impulse. However, it only took about 24 hours for someone to email me to point out that it’s NOT typical to use an impulse to do an impulse response measurement.

These days, that is true. In the old days, it was pretty normal to do an impulse response measurement of a room by firing a gun or popping a balloon. However, unless your impulse is really loud, this method suffers from a low signal-to-noise ratio.

So, these days, mainly to get a better signal-to-noise ratio, we typically use another kind of signal that can be turned into an impulse response using a little clever math. One method is to send a Maximum Length Sequence (or MLS) through the device. The other method uses a sine wave with a smoothly swept-frequency.

There are other ways to do it, but these two are the most common for reasons that I won’t get into.

In both the MLS and the swept-sine cases, you take the incoming signal from the DUT, and do some math that compares the outgoing signal to the incoming signal and converts the result into an impulse response. You can then use that to do your analyses of the linear response of the DUT.

If your DUT is behaving perfectly linearly, then this will work fine. However, if your DUT has some kind of non-linear distortion, then the effects of the distortion on the measurement signal will result in some kinds of artefacts that show up in the impulse response in a potentially non-intuitive way.

This series of postings is going to be a set of illustrations of these artefacts for different types of distortion. For the most part, I’m not going to try to explain why the artefacts look the way they do. It’s just a bunch of illustrations that might help you to recognise the artefacts in the future and to help you make better choices about how you’re doing the measurements in the first place.

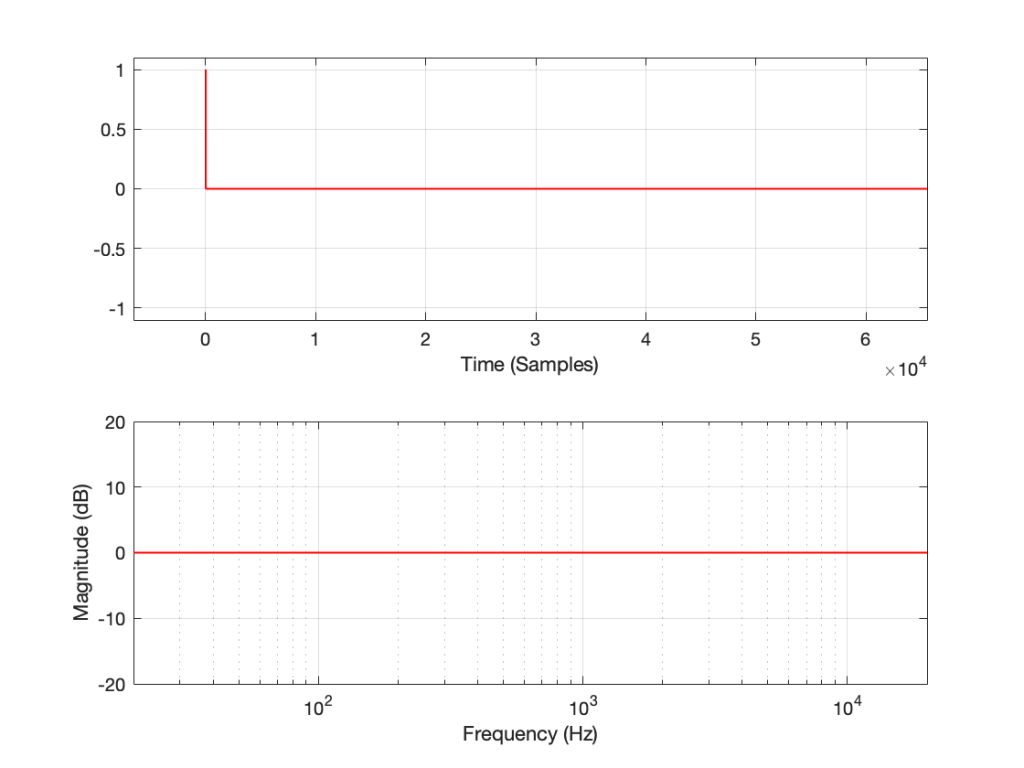
:To start, let’s take a “perfect” DUT and

measure its impulse response using the three methods (impulse, MLS, and swept sine)
for the MLS and swept sine methods, convert the incoming signal to an impulse response and plot it
find the magnitude response of the impulse response via an FFT and plot that

The results of these three measurement methods are shown below:

If you believe in conspiracy theories, then you might be suspicious that I actually just put up the same plot three times and changed the caption, but you’ll have to trust me. I didn’t do that. I actually ran the measurement three times.

If you’re familiar with the MLS and/or swept sine techniques, then you’ll be interested in a little more information:

The sampling rate is 48 kHz
Calculating in a floating point world with lots of resolution (I’m doing this all in Matlab and I’m not quantising anything… yet…)
The MLS signal is 2^16 samples long
I’m using one MLS sequence (for now)
I am not averaging the MLS measurement. I just ran it once.
The swept sine starts at 1 Hz and runs for 10 seconds.
For both the MLS and the sine sweep, I’m applying a pre-emphasis filter to the signal sent to the DUT and a reciprocal de-emphasis filter to the signal coming from it. This puts a bass-heavy tilt on the signal to be more like the spectrum of music. However, it’s not a “pinking” filter, which would cause a loss of SNR due to the frequency-domain slope starting at too low a frequency.
My DUT isn’t really a device. It’s just code that I’m applying to the signal, so there’s no input or output via some transmission system like analogue cabling, for example…

Most of that will be true for the other parts of the rest of the series. When it’s not true, I’ll mention it.

It’s not acoustics, but it’s close

Development of Beolab 90

#94 in a series of articles about the technology behind Bang & Olufsen

This was an online lecture that I did for the UK section of the Audio Engineering Society.

Excruciating minutiae: Part 3

In Part 2 of this series, I wrote the following sentence:

The easiest (and possibly best) way to do this is to create white noise with a triangular probability distribution function and a peak-to-peak amplitude of ± 1 quantisation level.

That’s a very busy sentence, so let’s unpack it a little.

Rolling the dice

If you roll one die, you have an equal probability of rolling any number between 1 and 6 (inclusive). Let’s roll one die 100 times counting the number of times we get a 1, or a 2, or a 3, and so on up to 6.

Number rolled	Number of times the number was rolled	Percentage of times the number was rolled
1	17	17
2	14	14
3	15	15
4	15	15
5	21	21
6	18	18

(Note that the percentage of times each number was rolled is the same as the number of times each number was rolled only because I rolled the die 100 times.)

If I plot those results, it looks like Figure 1.

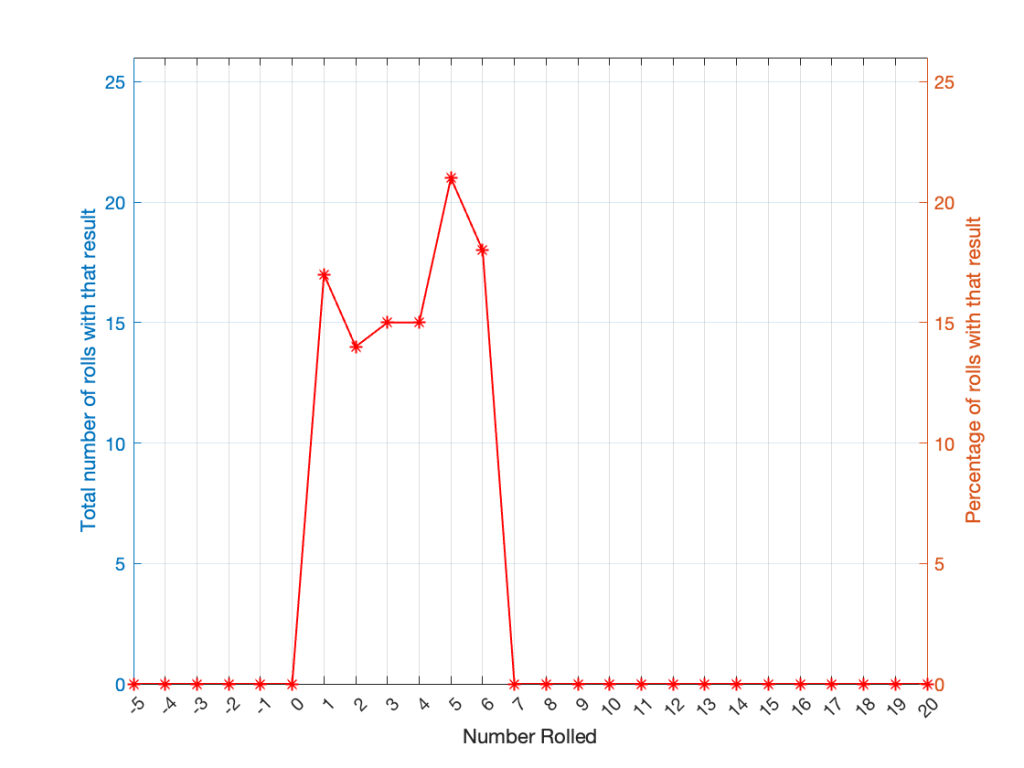
Figure 1. The results of rolling 1 die 100 times.

It may be weird, but I’ve plotted the number of times I rolled -5 or 13 (for example). These are 0 times because it’s impossible to get those numbers by rolling one die. But the reason I put those results in there will make more sense later.

Let’s keep rolling the die. If I do it 1,000,000 times instead of 100, I get these results:

ed	Number of times the number was rolled	Percentage of times the number was rolled
1	166225	16.6225
2	166400	16.6400
3	166930	16.6930
4	167055	16.7055
5	166501	16.6501
6	166889	16.6889

Now, since I rolled many, many, more times, it’s more obvious that the six results have an equal probability. The more I roll the die, the more those numbers get closer and closer to each other.

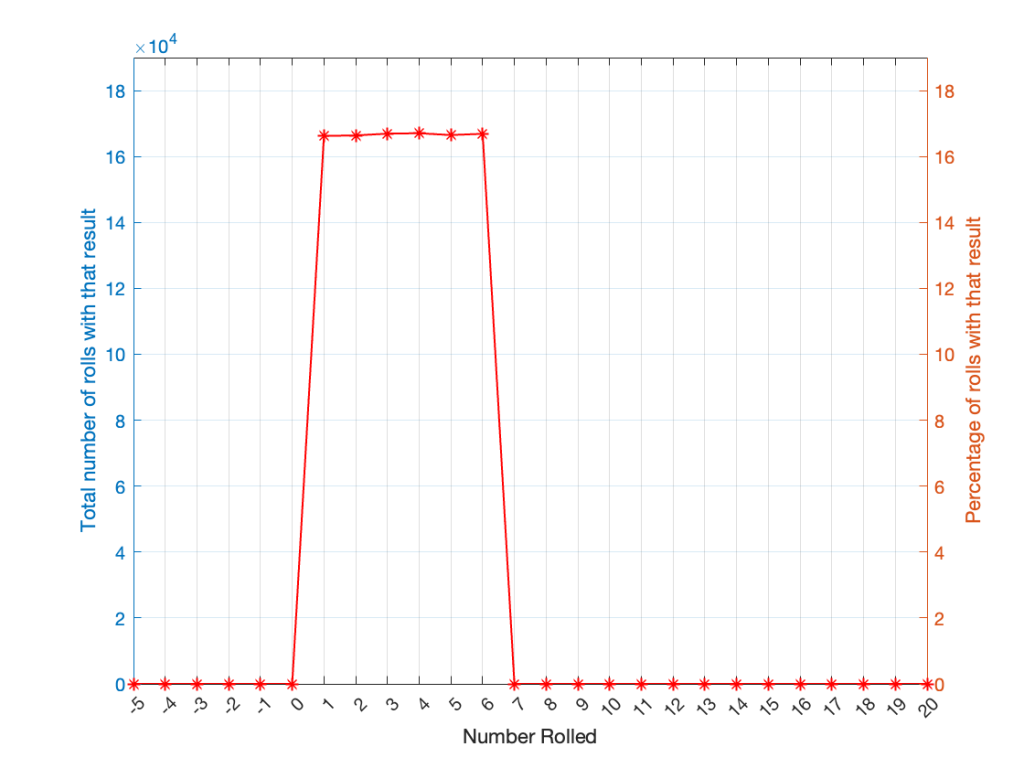
Take a look at the shape of the plot above. The area under the line from 1 to 6 (inclusive) is almost a rectangle because the six numbers are all almost the same.

The shape of that plot shows us the probability of rolling the six numbers on the die, so we call it a probability density function or PDF. In this case, we see a rectangular PDF.

But what happens if we roll two dice instead? Now things get a little more complicated, since there is more than one way to get a total result, as shown in the table below.

Total
2	1+1
3	1+2	2+1
4	1+3	2+2	3+1
5	1+4	2+3	3+2	4+1
6	1+5	2+4	3+3	4+2	5+1
7	1+6	2+5	3+4	4+3	5+2	6+1
8		2+6	3+5	4+4	5+3	6+2
9			3+6	4+5	5+4	6+3
10				4+6	5+5	6+4
11					5+6	6+5
12						6+6

As can be (hopefully) seen in the table, there is only one way to roll a 2, and there’s only one way to roll a 12. But there are 6 different ways to roll a 7. Therefore, if you’re rolling two dice, it’s 6 times more likely that you’ll roll a 7 than a 12, for example.

If I were to roll two dice 1,000,000 times, I would get a PDF like the one shown in Figure 3.

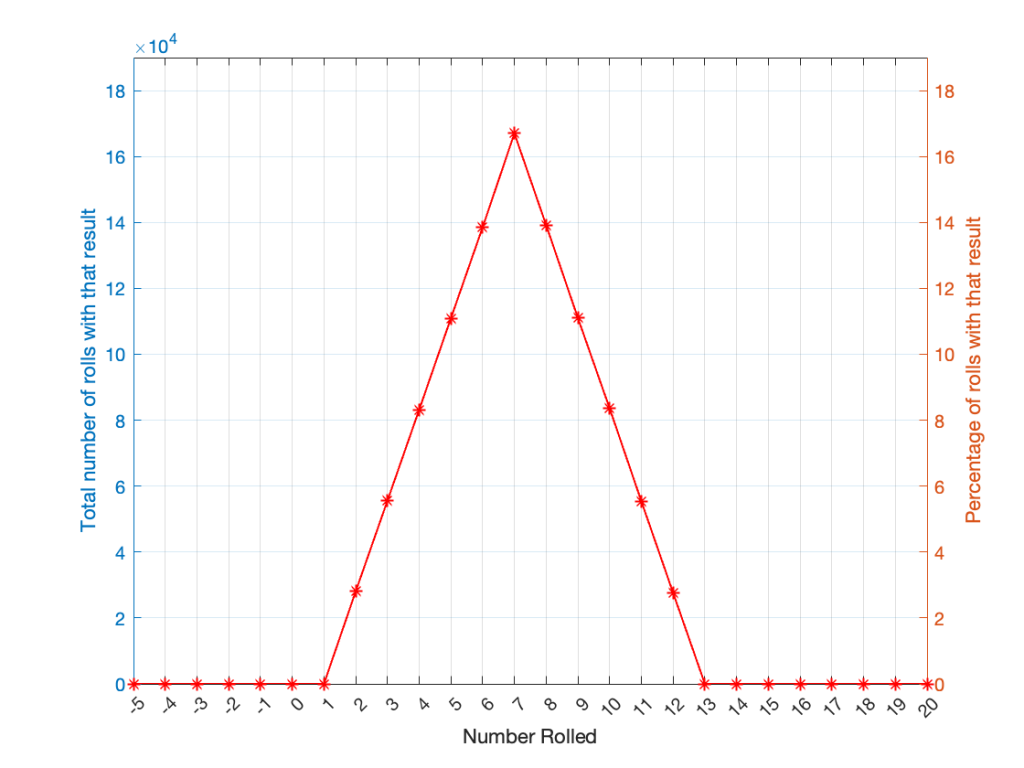
I won’t explain why this would be considered to be a triangular PDF.

Whether you roll one die or two dice, the number you get is random. In other words, you can’t use the past results to predict what the next number will be. However, if you are rolling one die, and you bet that you’ll roll a 6 every time, you’ll be right about 16.7% of the time. If you’re rolling two dice and you bet that you’ll roll a 12 every time, you’ll only be right about 2.8% of the time.

Let’s take two dice of different colours, say, one red die and one blue die. We’ll roll both dice again, but instead of adding the two values, we’ll subtract the blue value from the red one. If we do this 1,000,000 times, we’ll get something like the results shown below in Figure 4.

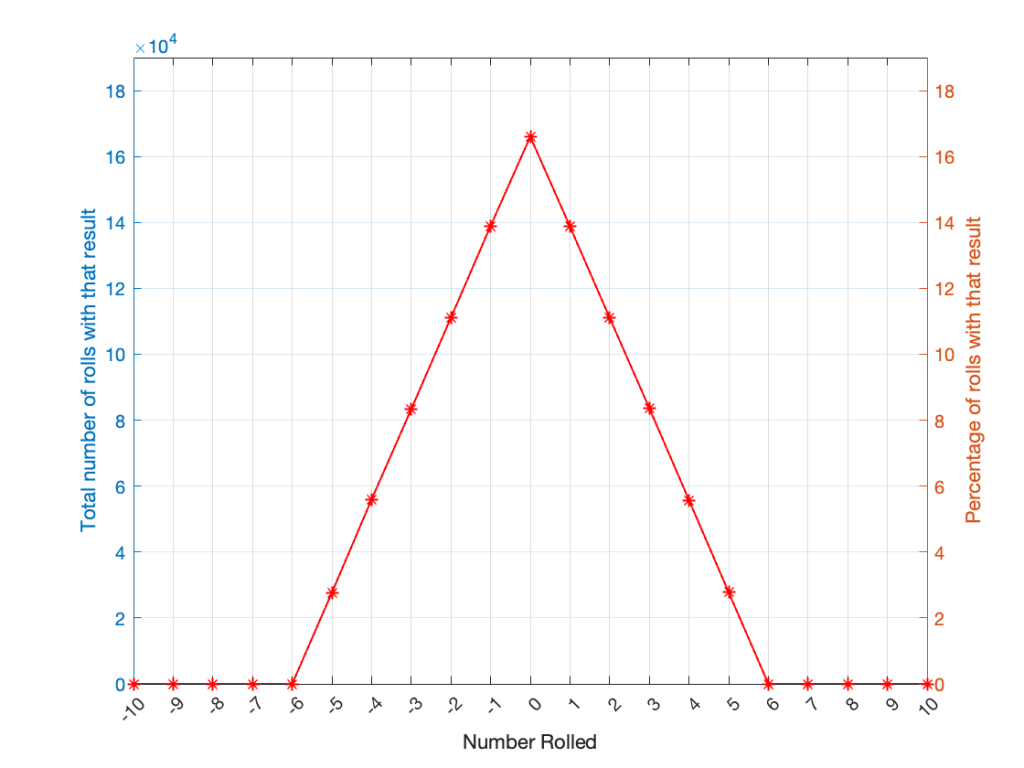
Notice that the probability density function keeps the same shape, it’s just moved down to a range of ±5 instead of 2 to 12.

Generating noise

In audio, noise is a sound that is completely random. In other words, just like the example with the dice, in a digital audio signal, you can’t predict what the next sample value will be based on the past sample values. However, there are many different ways of generating that random number and manipulating its characteristics.

Let’s start with a computer algorithm that can generate a random number between 0 and 1 (inclusive) with a rectangular PDF. We’ll then ask the algorithm to spit out 1,000,000 values. If the numbers really are random, and the computer has infinite precision, then we’ll probably get 1,000,000 different numbers. However, we’re not really interested in the numbers themselves – we’re interested in how they’re distributed between 0.00 and 1.00. Let’s say we divide up that range into 100 steps (or “buckets”) that are 0.01 wide and count how many of our random numbers fall into each group. So, we’ll count how many are between 0.0 and 0.01, between 0.01 and 0.02, and so on up to 0.99 to 1.00. We’ll get something like Figure 5.

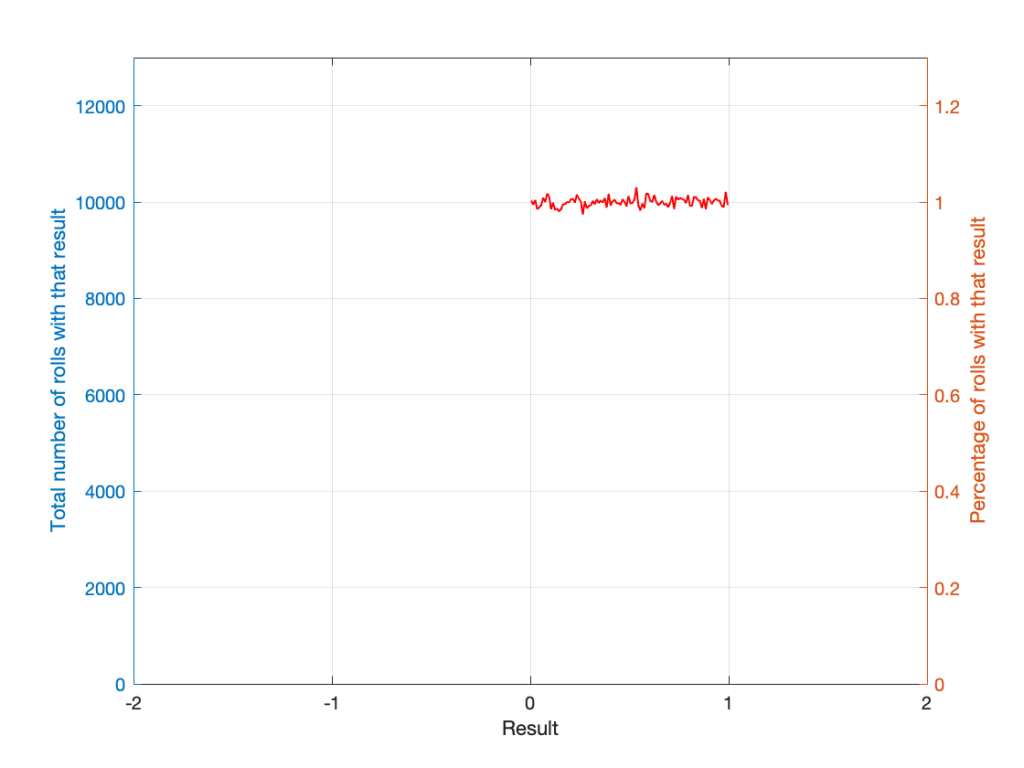
I’ve only plotted the probabilities of the possible values: 0 to 1, which winds up showing only the top of the rectangle in the rectangular PDF.

If I generate 1,000,000 random numbers with that algorithm, and then subtract 1,000,000 other random numbers, one by one, and find the probabilities of the result, the answer will be familiar.

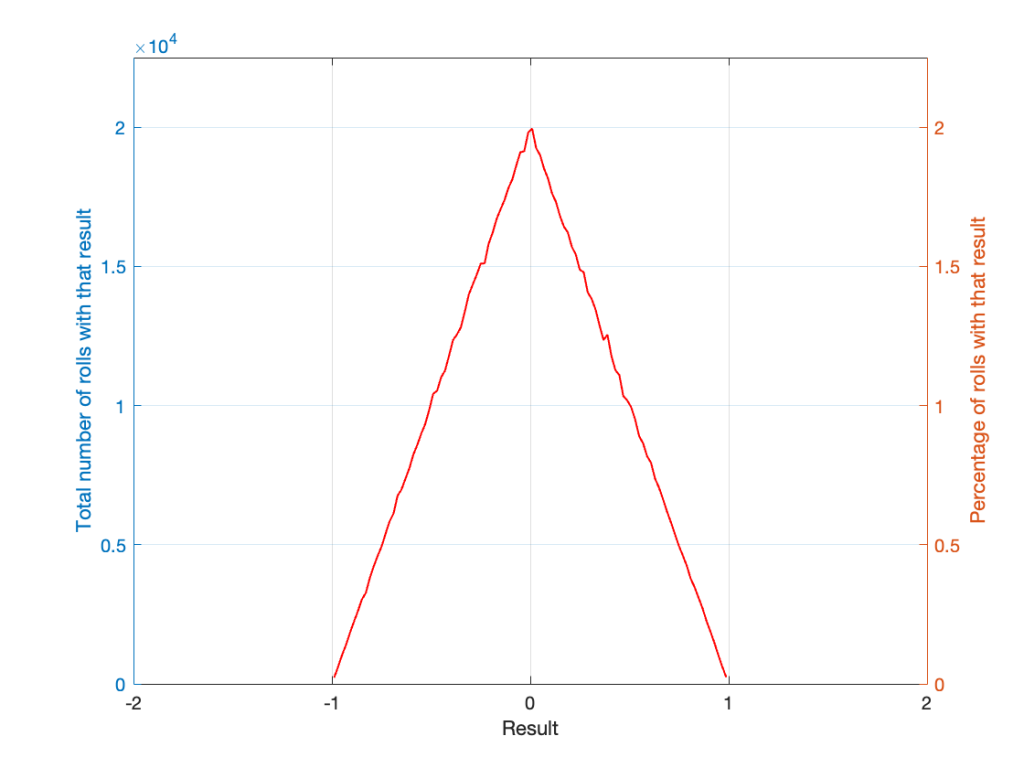
So, this is how we make the noise that’s added to the signal. If, for each sample, you generate two random numbers (making sure that your algorithm has a rectangular PDF) and subtract one from the other, you have the dither signal that will have a maximum level of ±1 quantisation level.

The signal (with a maximum range of ±1) is scaled up by multiplying it by 2^{(NumberOfBits-1)}-2
then you add the result of the dither generator
then the total is rounded to the nearest integer value
and then the result is scaled back down by a factor of 2^{(NumberOfBits-1)} to bring its back down to a range of ±1 to get it ready for exporting to a standard audio file format like .wav or .flac.

In other words, assuming that you have an audio signal called “Signal” that has a range of ±1 and consists of floating point values:

ScaleUp = 2^(Bitdepth-1)-2
ScaleDown = 2^(Bitdepth-1)

TpdfDither = rand(LengthOfSignal) - rand(LengthOfSignal) 

QuantisedDitheredSignal = round(Signal * ScaleUp + TpdfDither) / ScaleDown;

Excruciating minutiae: Part 2

In Part 1, I talked about how an audio signal is quantised, and how the world that the quantised signal lives in is slightly asymmetrical.

Let’s stay in a 3-bit world (to keep things comprehensible on a human scale) and do some recreational quantisation. We’ll start by making a sine wave with a peak amplitude of 1. This means that the total range will be ±1.

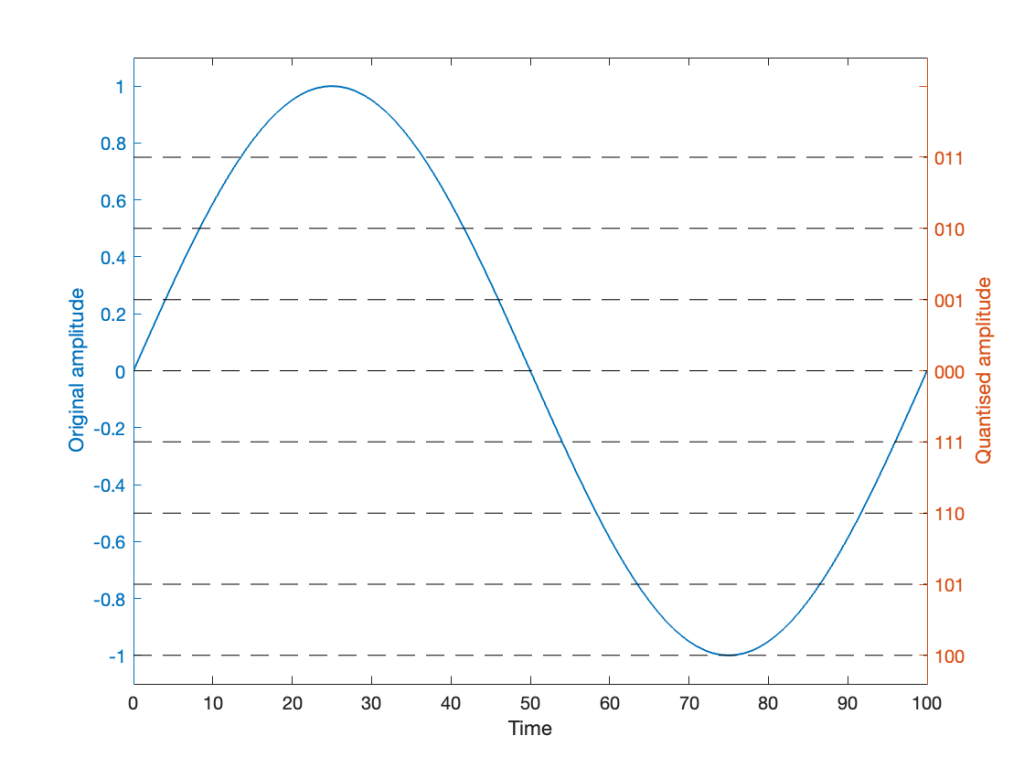
Figure 1. A sine wave with an amplitude of 1.

Notice that I put two scales on the plot in Figure 1. On the left, we have the “floating point” amplitude scale. On the right, we have the 8 quantisation levels.

If we are a bit dumb, and we just quantise that sine wave directly, making sure that I’ve aligned the scaling to use ALL possible quantisation values, we get the result in Figure 2.

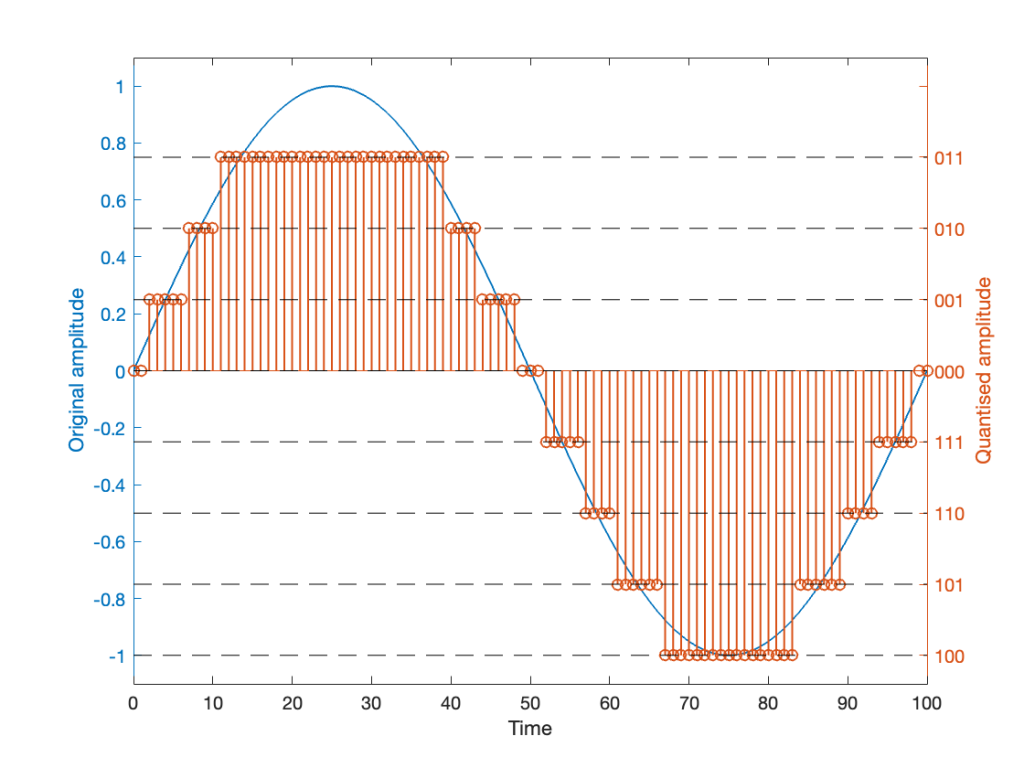
Figure 2. The original signal in blue and the quantised representation in red.

Notice that, because the original signal is symmetrical (with respect to positive and negative amplitudes) but the quantisation steps are not, we wind up getting a different result for the positive values than the negative values. In other words, after quantisation, I’ve clipped the positive peaks of the original signal.

Okay, so this is a dumb way to do this. A slightly less dumb way is to adjust the scaling so that the original wave does not use all possible quantisation values, as shown in Figure 3.

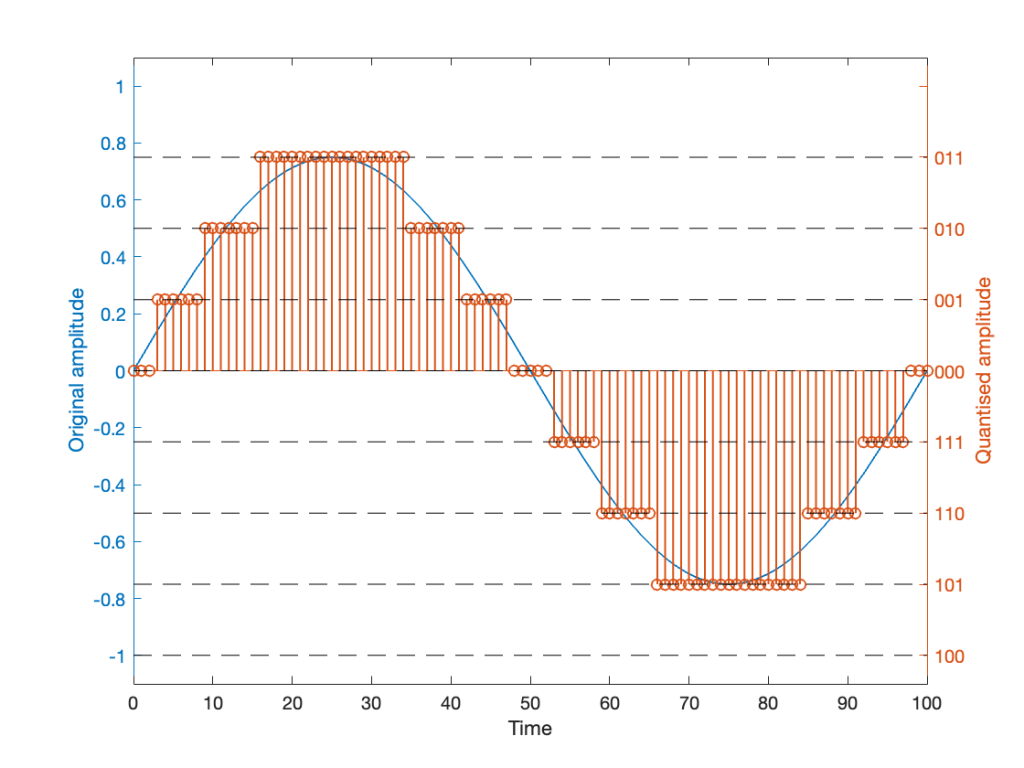
Notice that I’ve set the sine wave to a slightly lower level, so that it rounds to the top-most positive quantisation level, but this means that it doesn’t use the lowest negative quantisation level. If we’re being really picky, I could have made the sine wave just a little higher in amplitude: by 1/2 of a quantisation step, and the quantised result would still not have clipped asymmetrically.

Dither

As you can see in Figures 2 and 3 above, just taking a signal and quantising it generates an error. The more bits you have in the word length, the more quantisation levels you have, and the smaller the error. However, that error will always be correlated with the signal somehow, and as a result, it’s distortion, which is easy to learn to hear.

If, however, we add a little noise to the signal before we quantise it, then we can randomise the error, which changes the error from producing distortion to a constant signal-independent noise floor. Since the noise makes the quantiser appear to be indecisive, we call it dither.

The easiest (and possibly best) way to do this is to create white noise with a triangular probability distribution function and a peak-to-peak amplitude of ± 1 quantisation level. I’ll explain what that last sentence means in Part 3 of this series.

If we do this, then we

take the signal
add a little noise to it
quantise it

and the result might look like Figure 4.

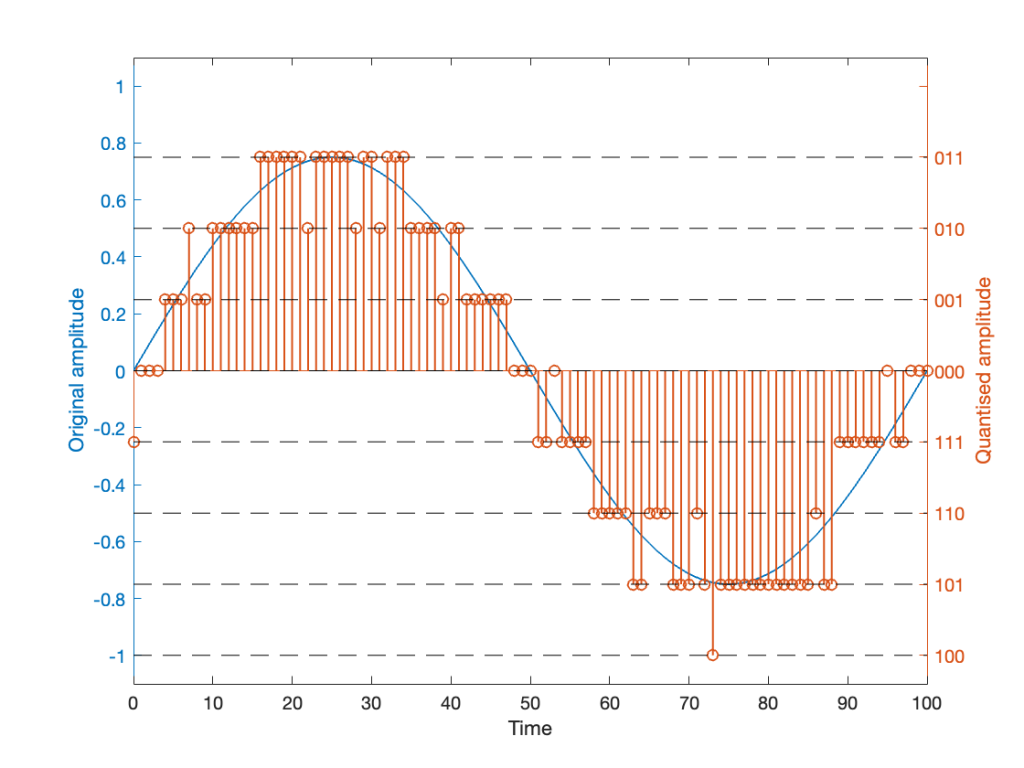
It should be easy to see that we still have quantisation, and also that I’ve added some random element to the signal.

However, let’s look at the mistake I made in Figure 4. The noise that was added to the signal has an amplitude of ±1 quantisation level. So, we should see cases where the signal looks like it should be rounding to the closest level, but it might be either 1 above or 1 below. (For example, take a look at Time = 70, 71, and 72 as an example of this.)

However, take a look around Time = 20 to 30. Notice that the original signal is close to the top quantisation level. This means that, although a negative value in the dither in those samples can bring the quantisation level down, a positive value cannot bring it up because we don’t have any room for it. This will, again, result in a small amount of asymmetrical clipping. This is a VERY small amount. (Remember that, in the real world we’re probably using 2¹⁶ (= 65,536) or 2²⁴ (= 16,777,216) quantisation values, not 2³ (= 8).

So, if we’re going to avoid this clipping, we need to adjust the scaling of the signal once more, as shown in Figure 5.

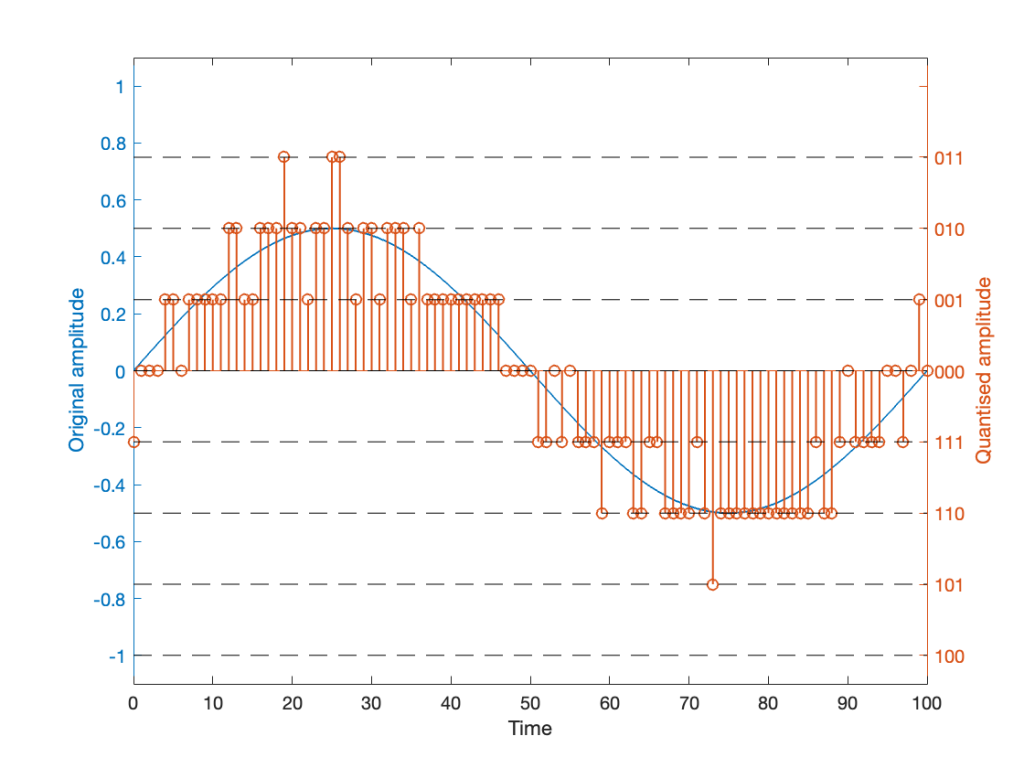
This shows a signal that is scaled so that, without dither, it would round to one level away from the top-most quantisation level. When you add the dither, it can go up to that top quantisation level. (In fact, I happened to use the same dither signal for Figures 4 and 5. The only difference is the scaling of the signal.)

Now, I know that if you’re not used to looking at 3-bit signals, and/or if dither is a new concept, the red signal in Figure 5 might make you a little upset. However (and you have to believe me on this…) this is the correct way to encode digital audio. Just because it looks crazy doesn’t mean that it is.

NB: The math

If you want to make the plots above, here’s a simplified version of the math to try it out. Note: I live in a world where a % symbol precedes a comment.

Some Constants

Bitdepth = 3
Fs = 100 % sampling rate in Hz
Fc = 1 % frequency of the sine wave in Hz
TimeInSamples = [0:Fs] % This will make the TimeInSamples all of the integer values from 0 to Fs (therefore, 1 second of audio)

Figure 1

Signal = sin(2 * pi * Fc/Fs * TimeInSamples)

Figure 2

ScaleUp = 2^(Bitdepth-1)
ScaleDown = 2^(Bitdepth-1)

QuantisedSignal = round(Signal * ScaleUp) / ScaleDown;

% Then apply a clipper to remove the top quantisation level.
% You can do this yourself.

Figure 3

ScaleUp = 2^(Bitdepth-1)-1
ScaleDown = 2^(Bitdepth-1)

QuantisedSignal = round(Signal * ScaleUp) / ScaleDown;

Figure 4

ScaleUp = 2^(Bitdepth-1)-1
ScaleDown = 2^(Bitdepth-1)
TpdfDither = rand(LengthOfSignal) - rand(LengthOfSignal)

QuantisedDitheredSignal = round(Signal * ScaleUp + TpdfDither) / ScaleDown;

% Then apply a clipper to remove the top quantisation level.

Figure 5

ScaleUp = 2^(Bitdepth-1)-2
ScaleDown = 2^(Bitdepth-1)
TpdfDither = rand(LengthOfSignal) - rand(LengthOfSignal)

QuantisedDitheredSignal = round(Signal * ScaleUp + TpdfDither) / ScaleDown;

Excruciating minutiae: Part 1

This past week I found a very small oddity in the behaviour of one of the functions in Matlab. This led me down a rabbit hole that I’m still following, but the stuff I’ve learned along the way has proven to be interesting.

The summary

The short version of the story is that I made a test tone which consisted of a sine wave that had a frequency that matched an FFT bin centre so that I could test a thing. In order to get the sine wave through the thing, I had to export the audio signal as something the thing could play. So, I exported it as both a .wav and a .flac file, both with 24-bit word lengths and matching sampling rates.

Once the two signals came back from the thing, they looked different on an FFT analysis. Not very different, but different enough to raise questions. So, I ran the FFT on the .wav and .flac files that I created to do the test and found out that THEY were different, which I didn’t expect, because I know that FLAC is lossless.

The question that came up first was “why are they different?”, and that was just the entrance to the rabbit hole.

The long version

In order to explain what happened, we have to following some advice given by Carl Sagan who said

‘If you wish to make an apple pie from scratch, you must first invent the universe.’

We won’t invent the universe, but we’re going to dig down into the basics of LPCM digital audio in order to come back up to talk about where I wound up last Thursday.

Quantisation

Linear Pulse Code Modulation (LPCM) is a way of encoding signals (like an audio signal) by saving the waveform as a series of measurements of the instantaneous amplitude. However, when you do this, you can’t have a measurement with an infinite resolution, so you have to round off the value to the nearest one you can encode. This is just like measuring something with a ruler that has millimetres marked on it. You can’t really measuring something with a precision of less than the nearest millimetre, so you round off the value to something you know. Whether or not that’s good enough depends on what the measurement is for.

In LPCM digital audio, we call the steps that you can round the values to ‘quantisation levels’ because you’re dividing up the amplitude into discrete quanta. Since the values of those quantisation levels are stored or transmitted using a binary number (containing only 0s and 1s), the number of quantisation levels is a power of 2. For example, if you have a 16-bit (bit = Binary digIT) value, then you can count from

0000 0000 0000 0000 = 0
to
1111 1111 1111 1111 = 2¹⁶ = 65,536

However, since audio signals go above and below 0 (we need to represent positive and negative values) we need a way to split up those options above (a range of 0 to 65,536) to do this.

Let’s take a simple example with a 3-bit long word. Since there are 3 bits, we have 2³ = 8 quantisation levels. It would be nice if 000 in the binary representation referred to a signal value of 0, like this:

All we need to do now is to figure out what binary values to put on the other quantisation levels. To do this, we use a system like the one shown in Figure 2.

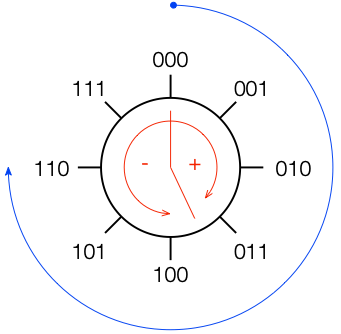
If you start at the top, and follow the blue circular arrow going clockwise, you count from 000 ( = 0) all the way to 111 (= 7). However, if you look at the red arrows, you can see that we can assign the binary values to the positive and negative quantisation levels by looking at the circle clockwise for positive values and counter-clockwise for negative ones. This means that we wind up with the assignments shown in Figure 3.

This way of using ‘wrapping’ the values around the circle into number assignments on a one-dimensional (in this case, vertical) scale is called a ‘two’s complement’ method.

There are two nice things about this system:

the middle value of 0 is assigned an actual value of 0, which makes sense to us humans
the first bit (digit) in the binary value tells you whether the level is positive (if it’s a 0) or negative (if it’s a 1).

There is at least one slightly annoying thing about this system: it’s asymmetrical. Notice in Figure 3 that there are 3 available positive quantisation levels, but 4 negative ones. This is because we have an even number of values to use (because it’s a power of 2) but one of the values is 0, leaving an odd, and therefore asymmetrical number of remaining values for the non-0 quantisation levels.

This will come back to be a pain in the arse later…

earfluff and eyecandy

mostly audio, but with some other stuff occasionally

Category: measurements