Normally, I don’t approve of homemade DIY speaker driver projects any more than I would approve of someone trying to build a breeder reactor from glow-in-the-dark watch parts in his backyard shed. However, this made for a fun read this morning…
Category: loudspeakers
B&O Tech: Native or not?
#62 in a series of articles about the technology behind Bang & Olufsen products
Over the past year or so, I’ve had lots of discussions and interviews with lots of people (customers, installers, and journalists) about Bang & Olufsen’s loudspeakers – BeoLab 90 in particular. One of the questions that comes up when the chat gets more technical is whether our loudspeakers use native sampling rates or sampling rate conversion – and why. So, this posting is an attempt to answer this – even if you’re not as geeky as the people who asked the question in the first place.
There are advantages and disadvantages to choosing one of those two strategies – but before we get to talk about some of them, we have to back up and cover some basics about digital audio in general. Feel free to skip this first section if you already know this stuff.
A very quick primer in digital audio
An audio signal in real life is a change in air pressure over time. As the pressure increases above the current barometric pressure, the air molecules are squeezed closer together than normal. If those molecules are sitting in your ear canal, then they will push your eardrum inwards. As the pressure decreases, the molecules move further apart, and your eardrum is pulled outwards. This back-and-forth movement of your eardrum starts a chain reaction that ends with an electrical signal in your brain.
If we take your head out of the way and replace it with a microphone, then it’s the diaphragm of the mic that moves inwards and outwards instead of your eardrum. This causes a chain reaction that results in a change in electrical voltage over time that is analogous to the movement of the diaphragm. In other words, as the diaphragm moves inwards (because the air pressure is higher), the voltage goes higher. As the diaphragm moves outwards (because the air pressure is lower) the voltage goes lower. So, if you were to plot the change in voltage over time, the shape of the plot would be similar to the change in air pressure over time.
We can do different things with that changing voltage – we could send it directly to a loudspeaker (maybe with a little boosting in between) to make a P.A. system for a rock concert. We could send it to a storage device like a little wiggling needle digging a groove in a cylinder made of wax. Or we could measure it repeatedly…
That last one is where we’re headed. Basically speaking, a continuous, analogue (because it’s analogous to the pressure signal) audio signal is converted into a digital audio signal by making instantaneous measurements of it repeatedly, and very quickly. It’s a little bit like the way a movie works: you move your hand and take a movie – the camera takes a bunch of still photographs in such quick succession that, if you play back the photos quickly, it looks like movement to our slow eyes. Of course, I’m leaving out a bunch of details, but that’s the basic concept.
So, a digital audio signal is a series of measurements of an electrical voltage (which was changing over time) that are transmitted or stored as numbers somehow, somewhere.
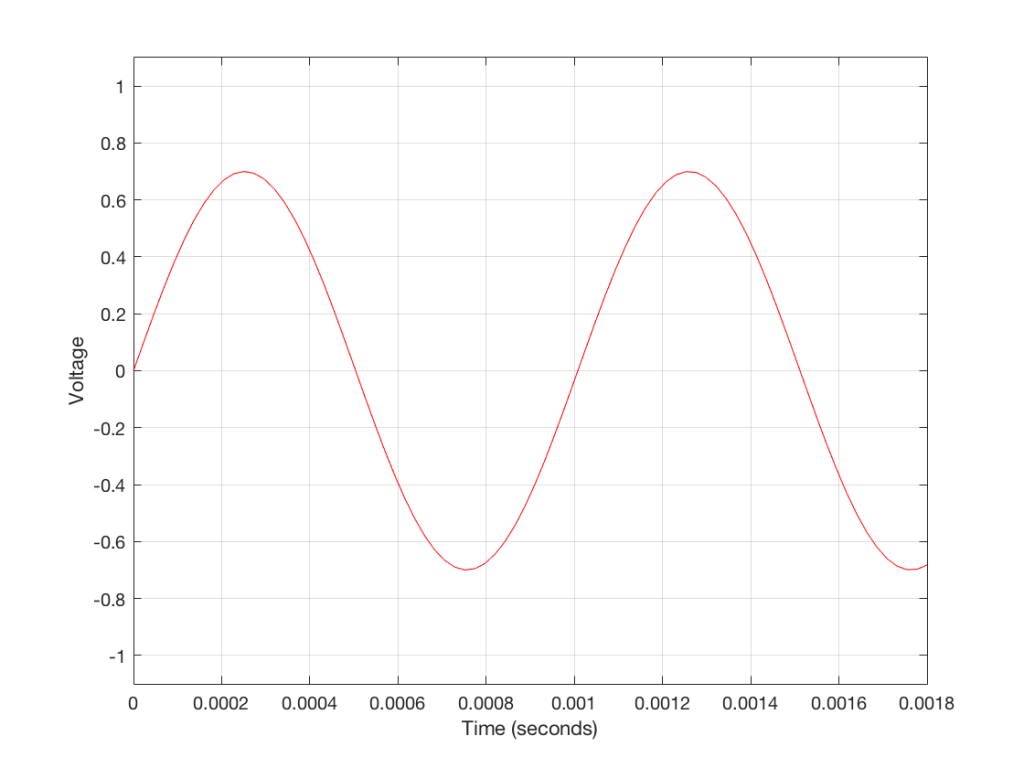
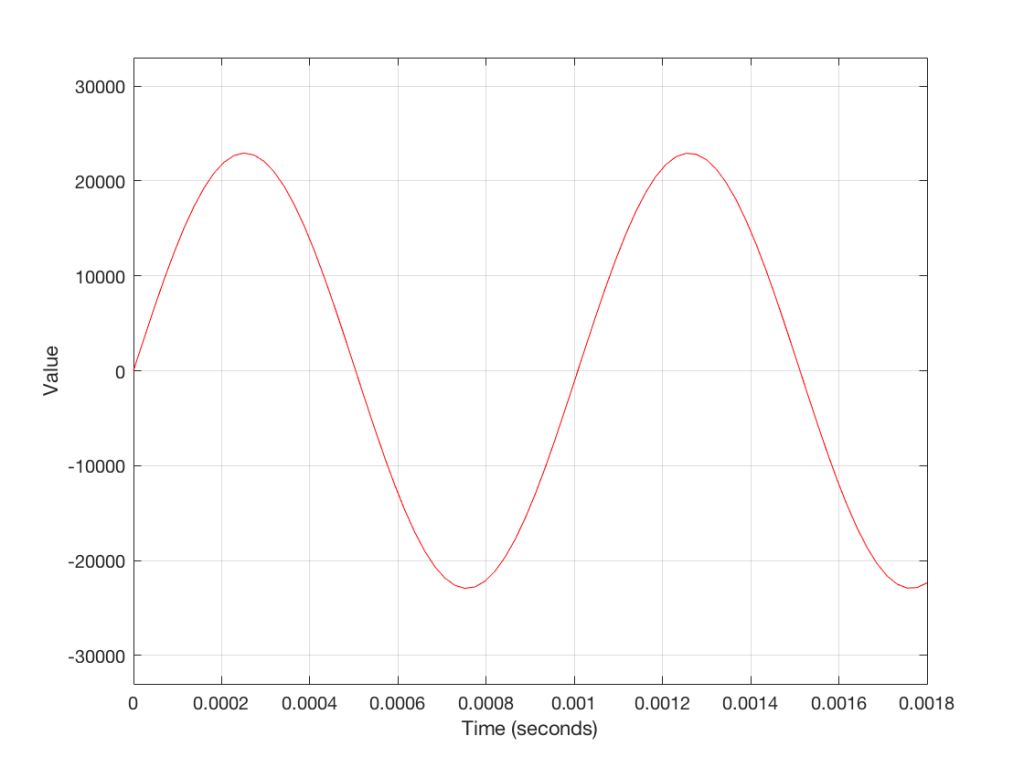
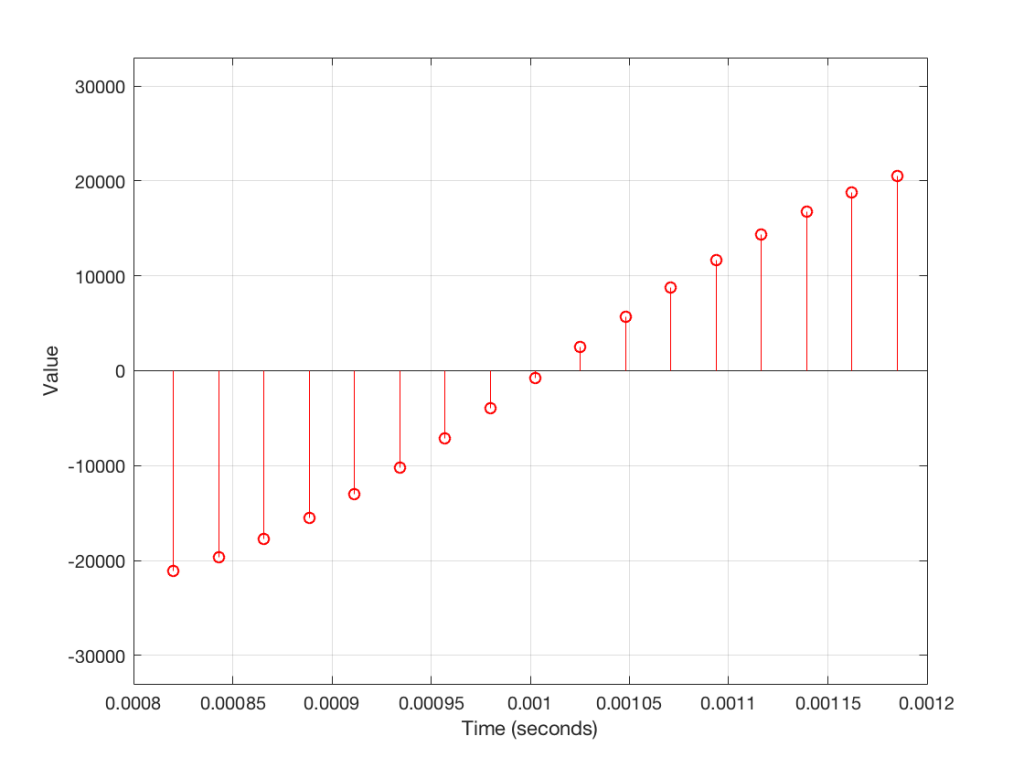
Figure 3 shows a small slice of time from Figure 2, which is, itself a small slice of time that normally is considered to extend infinitely into the past and the future. If we want to get really pedantic about this, I can tell you the actual values represented in the plot in Figure 3. These are as follows:
- -21115
- -19634
- -17757
- -15522
- -12975
- -10167
- -7153
- -3996
- -758
- 2495
- 5698
- 8786
- 11697
- 14373
- 16759
- 18807
- 20477
The actual values that I listed there really aren’t important. What is important is the concept that this list of numbers can be used to re-construct the signal. If I take that list and plot them, it would look like Figure 4.

So, in order to transmit or store an audio signal that has been converted from an analogue signal into a digital signal, all I need to do is to transmit or store the numbers in the right order. Then, if I want to play them back (say, out of loudspeaker) I just need to convert the numbers back to voltages in the right order at the right rate (just like a movie is played back at the same frame rate that the photos were take in – otherwise you get things moving too fast or too slowly).
One last piece of information that you’ll need before we move on is that, in a digital audio system, the audio signal can only contain reliable information below the frequency that is one-half of the “sampling rate” (which is the rate at which you are grabbing those measurements of the voltages – each of those measurements is called a “sample”, since it’s taking an instantaneous sample of the current state of the system). It’s just like taking a blood sample or a water sample – you use it as a measurement of one portion of one thing right now. This means that if you want to record and play back audio up to 20,000 Hz (or 20,000 cycles per second – which is what textbooks say that we can hear) you will need to be making more than 40,000 measurements per second. If we use a CD as an example, the sampling rate is 44,100 samples per second – also known as a sampling rate of 44.1 kHz. This is very fast.
Sidebar: Please don’t jump to conclusions about what I have said thus far. I am not saying that “digital audio is perfect” (or even “perfect-er or worse-er than analogue”) or that “this is all you need to understand how digital audio works”. And, if you are the type of person who worships at “The Church of Our Lady of Perpetual Jitter” or “The Temple of Inflationary Bitrates” please don’t email me with abuse. All I’m trying to do here is to set the scene for the discussion to follow. Anyone really interested in how digital audio really works should read the collected writings of Harry Nyquist, Claude Shannon, John Watkinson, Jamie Angus, Stanley Lipshitz, and John Vanderkooy and send them emails instead. (Also, if you’re one of the people that I just mentioned there, please don’t get mad at me for the deluge of spam you’re about to receive…)
Filtering an audio signal
Most loudspeakers contain a filter of some kind. Even in the simplest passive two-way loudspeaker, there is very likely a small circuit called a “crossover” that divides the analogue electrical audio signal so that the low frequencies go to the big driver (the woofer) and the higher frequencies go to the little driver (the tweeter). This circuit contains “filters” that have an input and an output – the output is a modified (or filtered) version of the input. For example, in a low-pass filter, the low frequencies are allowed to pass through it, and the higher frequencies are reduced in level (which makes it useful for sending signals to the woofer).
Once again over-simplifying, this is accomplished in an electrical circuit by playing with something called electrical impedance – a measure of how much the circuit impedes the flow of current to the next device. Some circuits will impede the flow of current if it’s alternating quickly (a high frequency) other circuits might impede the flow of current if it’s alternating slowly (a low frequency). Other circuits will do something else…
It is also possible to filter an audio signal when it is in the digital domain instead. We have the series of numbers (like the one above) and we can send these to a mathematical function which will change the values into other numbers to produce the desired characteristics (like a low-pass filter, for example).
As a simple example, if we take all of the values in the list above, and multiply them by 0.5 before converting them back to voltages, then the output level will be quieter. In other words, we’ve made a volume knob in the digital domain. Of course, it’s not a very good knob, since it’s stuck at one setting… but this isn’t a course in advanced DSP…
If you want to make something more exciting than a volume knob, the typical way of making an audio filter in the digital world is to use delays to mix the signal with delayed copies of itself. This can get very complicated, but let’s make a simple filter to illustrate…
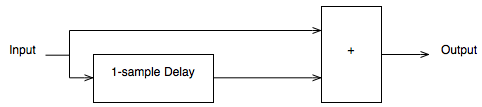
Figure 5 shows a very simple low pass filter for digital audio. Let’s think though what will happen when we send a signal through it.
If you have a very low frequency, then the current sample goes into the input and heads in two directions. Let’s ignore the top path for now and follow the lower path. The sample goes into a delay and comes out on the other side 1 sample later (in the case of a CD, this is 1/44100-th of a second later). When that sample comes out of the delay, the one that followed it (which is now “now” at the input) meets it at the block on the right with the “+” sign in it. This adds the two samples together and spits out of the result. In other words, the filter above adds the current audio sample to the previous audio sample and delivers the result as the current output.
What will this do to the audio signal?
If the frequency of the audio signal is very low, then the two samples (the current one, and the previous one) are very similar in level, as can be seen in the plot in Figures 6 and 7, below. This means, basically, that the output of the filter will be very, very similar to the output, just twice as loud (because it’s the signal plus itself). Another way to think of this is that the current sample of the audio signal and the previous sample of the same signal are essentially “in phase” – and any two audio signals that are “in phase” and added together will give you twice the output.
However, as the frequency of the audio signal gets higher, the relative levels of those two adjacent samples becomes more and more different (because the sampling rate doesn’t change). One of them will be closer to “0” than the other – and increasingly so as the frequency increases . So, the higher the audio frequency, the lower the level of the output (since it will not go higher than the signal plus itself, as we saw in the low frequency example…) If we’re thinking of this in terms of phase, the higher the frequency of the audio signal, the greater the phase difference between the adjacent samples that are summed, so the lower the output…
That output level keeps dropping as the audio frequency goes up until we hit a frequency where the audio signal’s frequency is exactly one half of the sampling rate. At that “magic point”, the two samples are so far apart (in terms of the audio signal’s waveform) that they have opposite polarity values (because they’re 180 degrees out-of-phase with each other). So, if you add those two samples together, you get no output – because they are equal, but opposite.
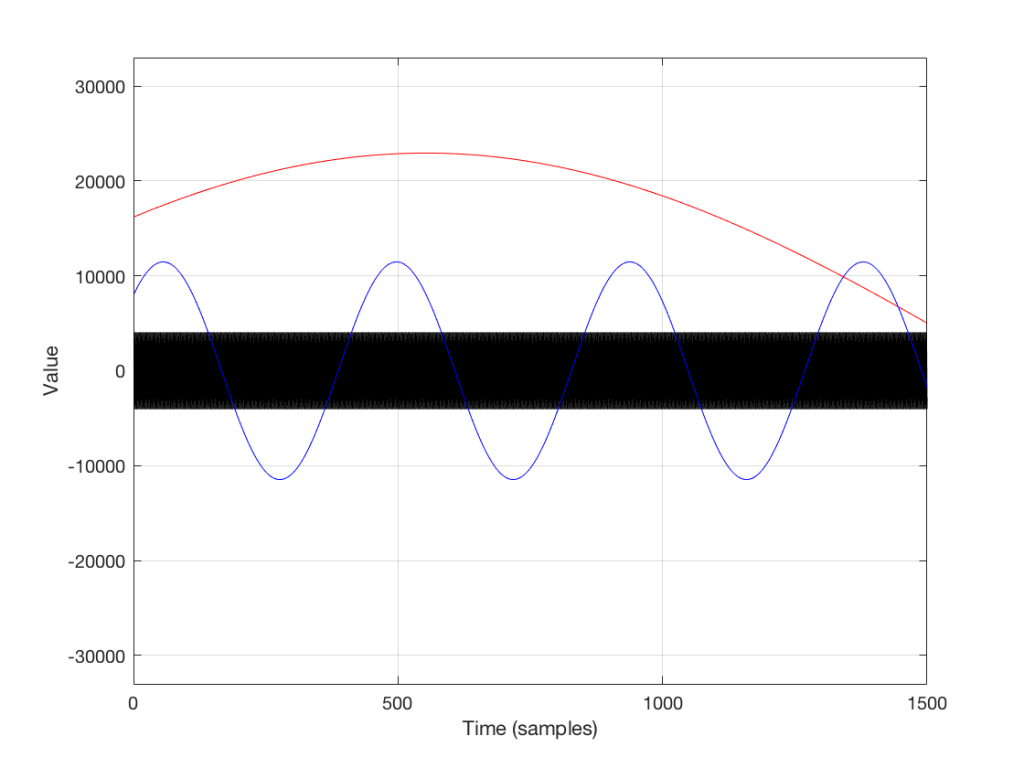
Let’s zoom in on the plot in Figure 6 to see the individual samples. We’ll take a slice of time around the 500-sample mark. This is shown below in Figure 7.
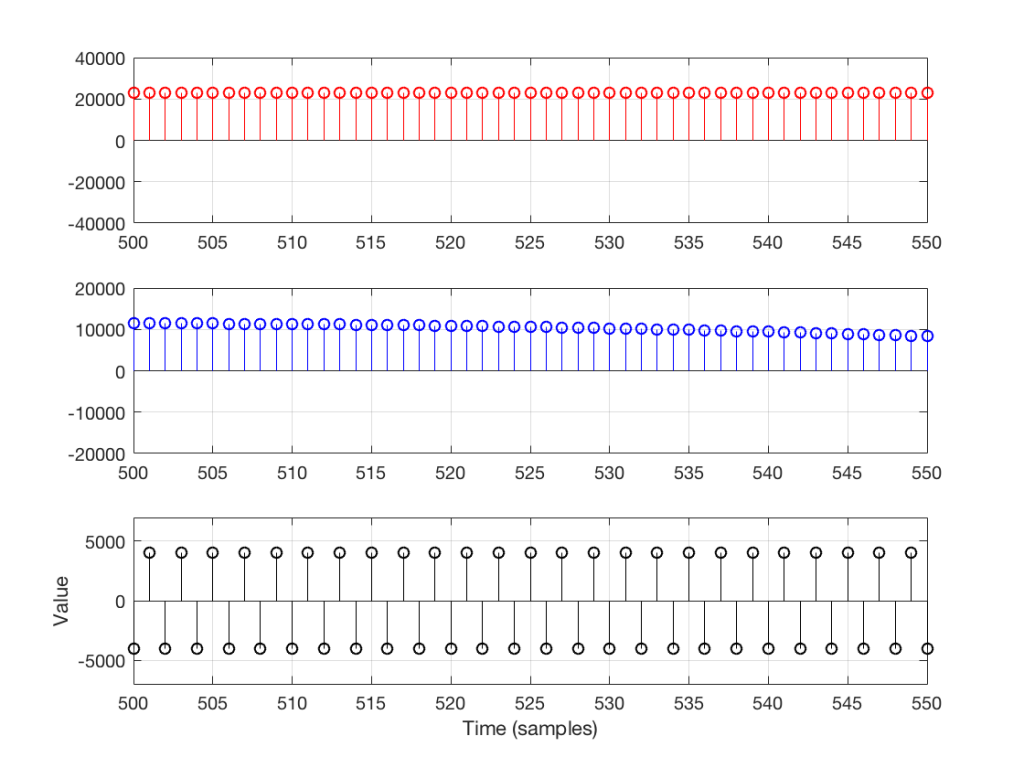
As you can see in Figure 7, any two adjacent samples for a low frequency (the red plot) are almost identical. The middle frequency (the blue plot) shows that two adjacent samples are more different than they are for this low frequency. For the “magic frequency” of “sampling rate divided by 2” (in this case, 22050 Hz) two adjacent samples are equal and opposite in polarity.
Now that you know this, we are able to “connect the dots” and plot the output levels for the filter in Figure 5 for a range of frequencies from very low to very high. This is shown in Figures 8 and 9, below.
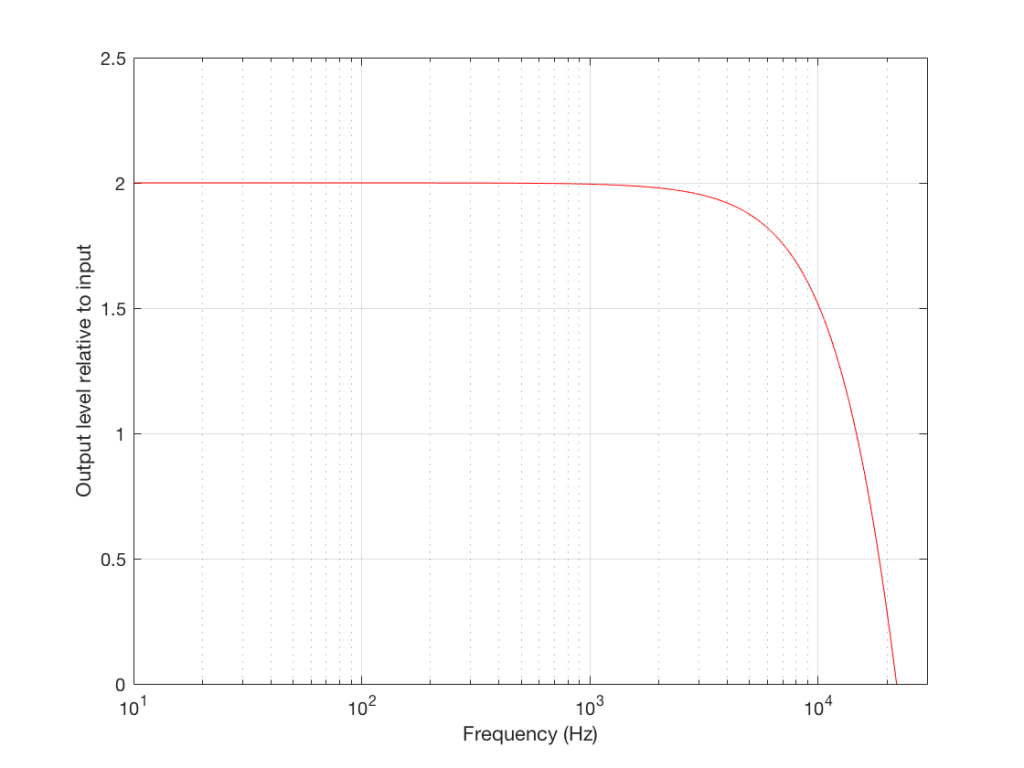
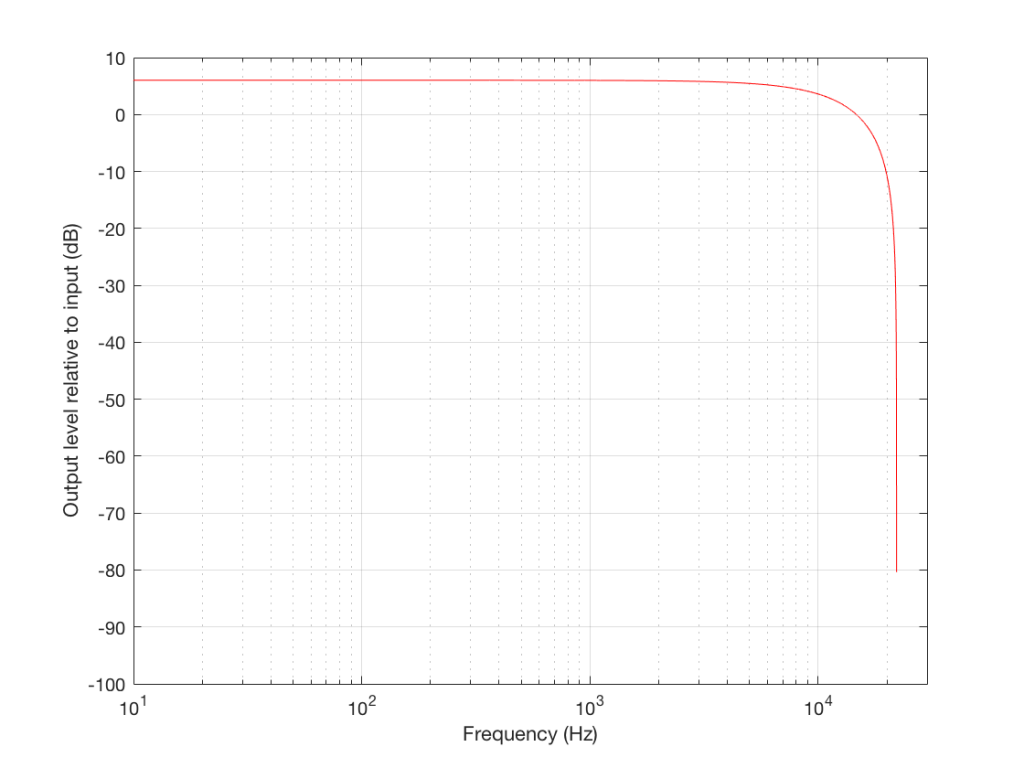
Normalised frequency
Now we have to step up the coefficient of geekiness…
So far, we have been thinking with a fixed sampling rate of 44.1 kHz – just like that which is used for a CD. However, audio recordings that you can buy online are available at different sampling rates – not just 44.1 kHz. So, how does this affect our understanding so far?
Well, things don’t change that much – we just have to change gears a little by making our frequency scales vary with sampling rate.
So, without using actual examples or numbers, we already know that an audio signal with a low frequency going through the filter above will come out louder than the input. We also know that the higher the frequency, the lower the output until we get to the point where the audio signal’s frequency is one half the sampling rate, where we get no output. This is true, regardless of the sampling rate – the only change is that, by changing the sampling rate, we change the actual frequencies that we’re talking about in the audio signal.
So, if the sampling rate is 44.1 kHz, we get no output at 22050 Hz. However, if the sampling rate were 96 kHz, we wouldn’t reach our “no output” frequency until the audio signal gets to 48 kHz (half of 96 kHz). If the sampling rate were 176.4 kHz, we would get something out of our filter up to 88.2 kHz.
So, the filter generally behaves the same – we’re just moving the frequency scale around.
So, instead of plotting the magnitude response of our filter with respect to the actual frequency of the audio signal out here in the real world, we can plot it with respect to the sampling rate, where we can get all the way up to 0.5 (half of the sampling rate) since this is as high as we’re allowed to go. So, I’ve re-plotted Figures 8 and 9 below using what is called a “normalised frequency” scale – where the frequency of the audio signal is expressed as a fraction of the sampling rate.
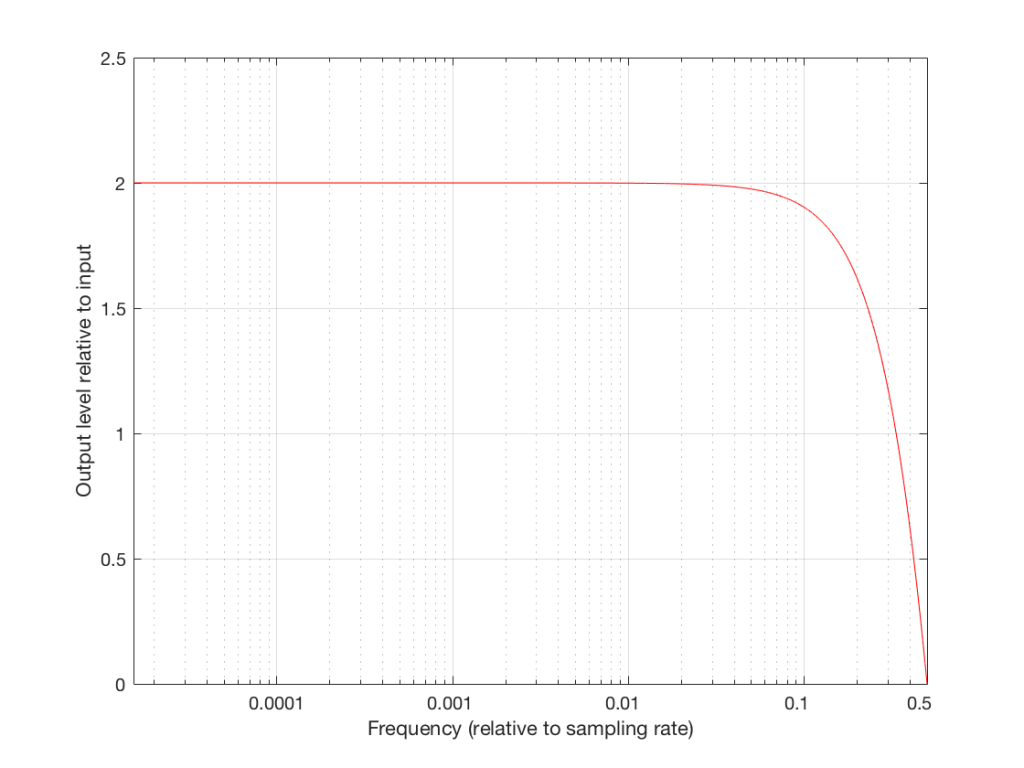
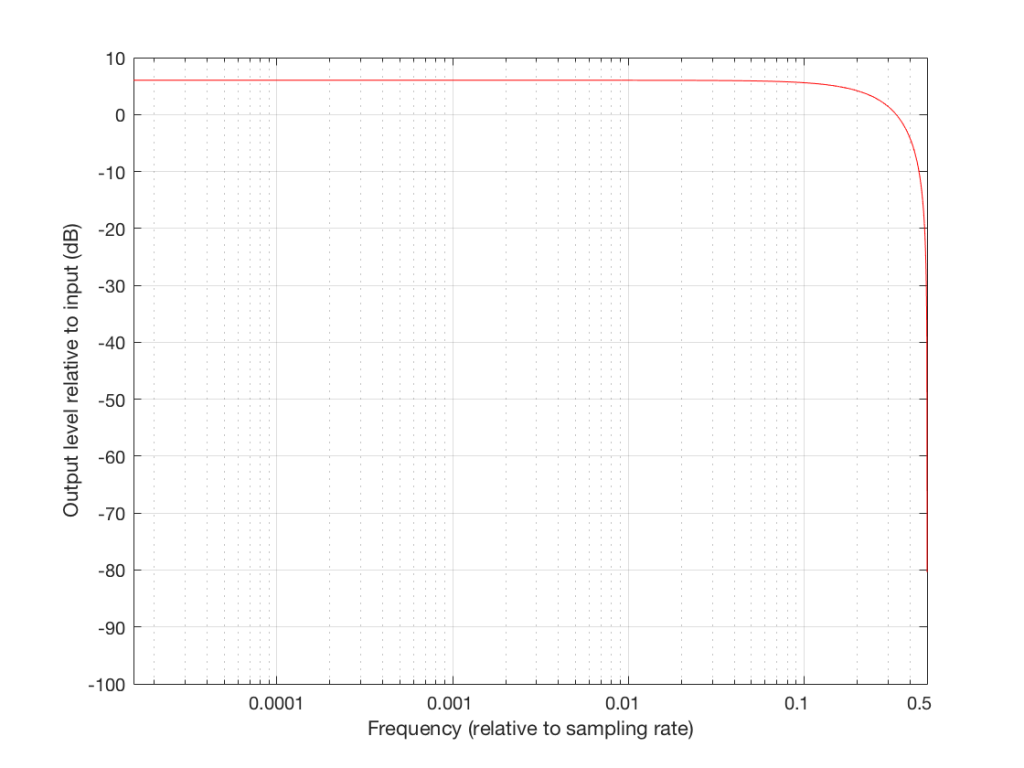
These last sentences are VERY IMPORTANT! So, if you didn’t understand everything I said in the previous 6 paragraphs, go back and read them again. If you still don’t understand it, please email me or put a comment in below, because it means that I didn’t explain it well enough. ..
Note that there are two conventions for “normalised frequency” just to confuse everyone. Some people say that it’s “audio frequency relative to the sampling rate” (like I’ve done here). Some other people say that it’s “audio frequency relative to half of the sampling rate”. Now you’ve been warned.
Designing an audio filter
In the example above, I made a basic audio filter, and then we looked at its output. Of course, if we’re making a loudspeaker with digital signal processing, we do the opposite. We have a target response that we want at the output, and we build a filter that delivers that result.
For example, let’s say that I wanted to make a filter that has a similar response to the one shown above, but I want it to roll off less in the high frequencies. How could I do this? One option is shown below in Figure 10:
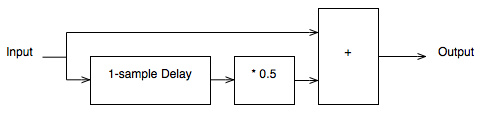
Notice that I added a multiplier on the output of the delay block. This means that if the frequency is low, I’ll add the current sample to half the value of the previous one, so I’ll get a maximum output of 1.5 times the input (instead of 2 like we had before). When we get to one half the sampling rate, we won’t cancel completely, so the high end won’t drop off as much. The resulting magnitude response is shown in Figures 11 and 12, below.
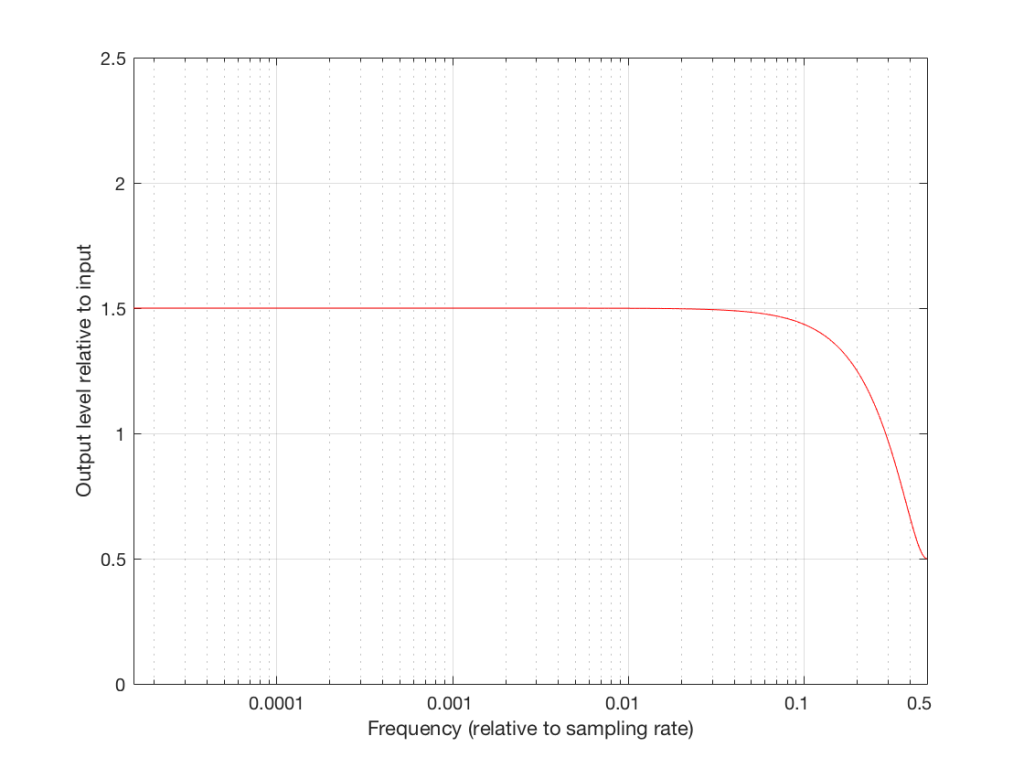
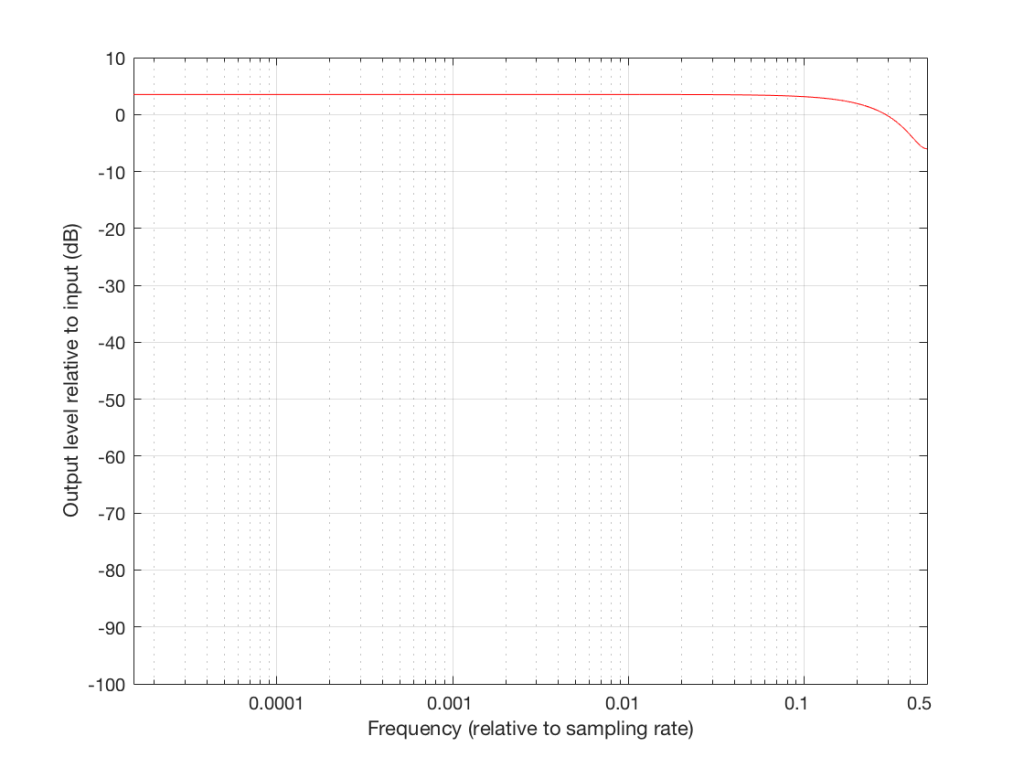
So, we can decide on a response for the filter, and we can design a filter that delivers that response. Part of the design of that filter is the values of the “coefficients” inside it. In the case of digital filters, “coefficient” is a fancy term meaning “number” – in the case of the filter in Figure 10, it has one coefficient – the “0.5” that is multiplied by the output of the delay. For example, if we wanted less of a roll-off in the high end, we could set that coefficient to 0.1, and we would get less cancellation at half the sampling rate (and less output in the low end….)
Putting some pieces together
So, now we see that a digital filter’s magnitude response (and phase response, and other things) is dependent on three things:
- its design (e.g. how many delays and additions)
- the sampling rate
- the coefficients inside it
If we change one of these three things, the magnitude response of the filter will change. This means that, if we want to change one of these things and keep the magnitude response, we’ll have to change at least one of the other things.
For example, if we want to change the sampling rate, but keep the design of the filter, in order to get the same sampling rate, we’re going to have to change the coefficients.
Again, those last two paragraphs were important… Read’em again if you didn’t get it.
So what?
Let’s now take this information into the real world.
In order for BeoLab 90 to work, we had to put a LOT of digital filters into it – and some of those filters contain thousands of coefficients… For example, when you’re changing from “Narrow” mode to “Wide” mode, you have to change a very large filter for each of loudspeaker driver (that’s thousands of coefficients times 18 drivers) – among other things… This has at least four implications:
- there has to be enough computing power inside the BeoLab 90 to make all those multiplications at the sampling rate (which, we’ve already seen above, is very fast)
- there has to be enough computer memory to handle all of the delays that are necessary to build the filters
- there has to be enough memory to store all of those coefficients (remember that they’re not numbers like 1 or 17 – they’re very precise numbers with a lot of digits like 0.010383285748578423049 (in case you’re wondering, that’s not an actual coefficient from one of the filters in a loudspeaker – I just randomly tapped on a bunch of keys on my keyboard until I got a long number… I’m just trying to make an intuitive point here…))
- You have to be able to move those coefficients from the memory where they’re stored into the calculator (the DSP) quickly because people don’t want to wait for a long time when you’re changing modes
This is why (for now, at least) when you switch between “Narrow” and “Wide” mode, there is a small “break” in the audio signal to give the processor time to load all the coefficients and get the signal going again.
One sneaky thing in the design of the system is that, internally, the processor is always running at the same sampling rate. So, if you have a source that is playing back audio files from your hard drive, one of them ripped from a CD (and therefore at 44.1 kHz) and the next one from www.theflybynighthighresaudiodownloadcompany.com (at 192 kHz), internally at the DSP, the BeoLab 90 will not change.
Why not? Well, if it did, we would have to load a whole new set of coefficients for all of the filters every time your player changes sampling rates, which, in a worst case, is happening for every song, but which you probably don’t even realise is happening – nor should you have to worry about it…
So, instead of storing a complete set of coefficients for each possible sampling rate – and loading a new set into the processor every time you switch to the next track (which, if you’re like my kids, happens after listening to the current song for no more than 5 seconds…) we keep the internal sampling rate constant.
There is a price to pay for this – we have to ensure that the conversion from the sampling rate of the source to the internal sampling rate of the BeoLab 90 is NOT the weakest link in the chain. This is why we chose a particular component (specifically the Texas Instruments SRC4392 – which is a chip that you can buy at your local sampling rate converter store) to do the job. It has very good specifications with respect to passband ripple, signal-to-noise ratio, and distortion to ensure that the conversion is clean. One cost of this choice was that its highest input sampling rate is 216 kHz – which is not as high as the “DXD” standard for audio (which runs at 384 kHz).
So, in the development meetings for BeoLab 90, we decided three things that are linked to each other.
- we would maintain a fixed internal sampling rate for the DSP, ADC’s and DAC’s.
- This meant that we would need a very good sampling rate converter for the digital inputs.
- The choice of component for #2 meant that BeoLab 90’s hardware does not support DXD at its digital inputs.
One of the added benefits to using a good sampling rate converter is that it also helps to attenuate artefacts caused by jitter originating at the audio source – but that discussion is outside the scope of this posting (since I’ve already said far too much…) However, if you’re curious about this, I can recommend a bunch of good reading material that has the added benefit of curing insomnia… Not unlike everything I’ve written here…
B&O Tech: The BeoLab 90 Story
#61 in a series of articles about the technology behind Bang & Olufsen products
B&O Tech: SoundStage InSight interview
#60 in a series of articles about the technology behind Bang & Olufsen products
more detailed info can be found in the links below:
- Beam Width Control
- Thermal Compression Compensation
- Active Room Compensation – Part 1 and Part 2
B&O Tech: 100 Years of Danish Loudspeakers
#56 in a series of articles about the technology behind Bang & Olufsen loudspeakers
This book was released some months ago as part of the 100 year anniversary of loudspeaker development in Denmark. There are a number of good articles in there, including a historical article on the importance of loudspeaker directivity at Bang & Olufsen.
Note that, unfortunately, the website that was associated with this book no longer exists… :-(

B&O Tech: A quick primer on distortion
#55 in a series of articles about the technology behind Bang & Olufsen loudspeakers
In a previous posting, I talked about the relationship between its “Bl” or “force factor” curve and the stiffness characteristics of its suspension and the fact that this relationship has an effect on the distortion characteristics of the driver. What was missing in that article was the details in the punchline – the “so what?” That’s what this posting is about – the effect of a particular kind of distortion in a system, and its resulting output.
WARNING: There is an intentional, fundamental error in many of the plots in this article. If you want to know about this, please jump to the “appendix” at the end. If you aren’t interested in the pedantic details, but are only curious about an intuitive understanding of the topic, then don’t worry about this, and read on. As an exciting third option, you could just read the article, and then read the appendix to find out how I’ve been protecting you from the truth…
Examples of Non-linear Distortion
Let’s start by looking at something called a “transfer function” – this is a plot of the difference between what you want and what you get.
For example, if we look at the excursion of a loudspeaker driver: we have some intended excursion (for example, we want to push the woofer out by 5 mm) and we have some actual excursion (hopefully, it’s also 5 mm…)
If we have a system that behaves exactly as we want it to within some limit, and then at that limit it can’t move farther, we have a system that clips the signal. For example, let’s say that we have a loudspeaker driver that can move perfectly (in other words, it goes exactly where we want it to) until it hits 5 mm from the rest position (either inwards or outwards). In this case, its transfer function would look like Figure 1.
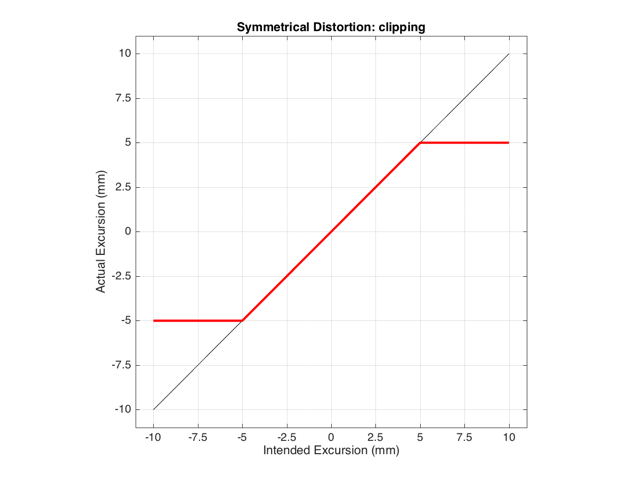
This means that if we try to move the driver with a sinusoidal wave that should peak at 10 mm and -10 mm, the tops and bottoms of the wave will be “chopped off” at ±5 mm. This is shown in Figure 2, below.

Let’s think carefully about the bottom plot in Figure 2. This is the difference between the actual excursion of the driver and the desired excursion (I calculated it by actually subtracting the top plot from the middle plot) – in other words, it’s the error in the signal. Another way to think of this is that the signal produced by the driver is what you want (the top plot) PLUS the error (the bottom plot). (Looking at the plots, if middle-top = bottom, then top+bottom = middle)
These plots show a rather simple case where the clipping of the signal is symmetrical. That is to say that the error on the positive part of the waveform is identical to that on the negative part of the waveform. As we saw in this posting, however, perfectly symmetrical distortion is not guaranteed… So, what happens if you have asymmetrical distortion? Let’s say, for example, that you have a system that behaves perfectly, except that it cannot move more than 5 mm outwards (moving inwards is not limited). The transfer function for this driver would look like Figure 3.
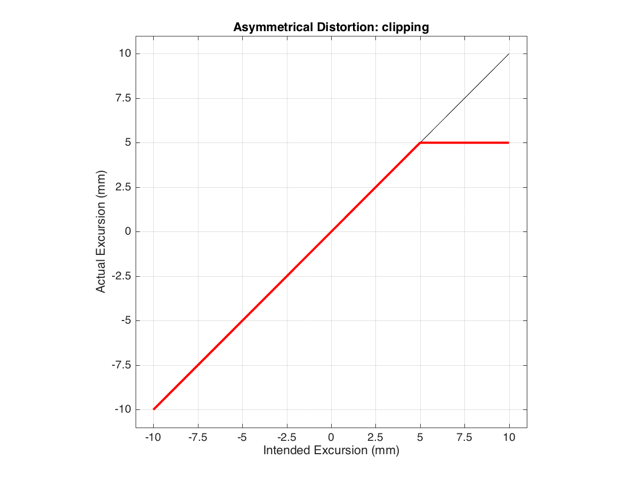
How would a sinusoidal waveform look if it were passed through that driver? This is shown in Figure 4, below.

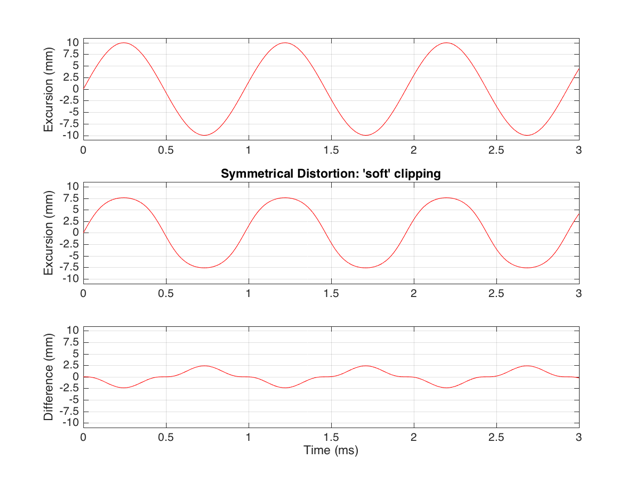
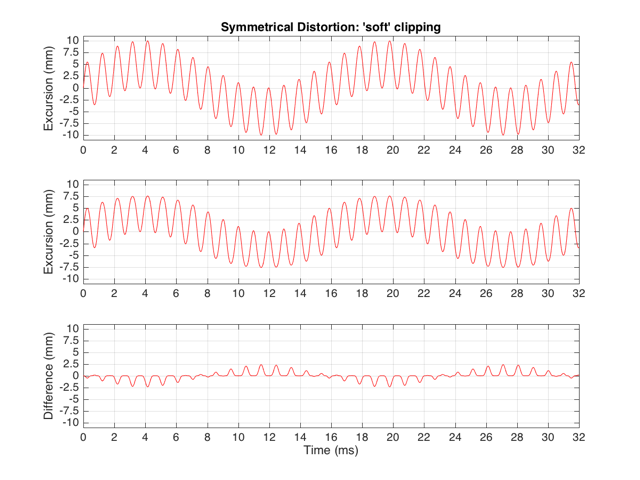
As we also saw before, it is unlikely that the abrupt clipping of a signal is how a real driver will behave. This is because, usually, a driver has an increasing stiffness and a decreasing force to push against it, as the excursion increases. So, instead of the driver behaving perfectly to some limit, and then clipping, it is more likely that the error is gradually increasing with excursion. An example of this is shown below in Figure 5. Note that this plot is just a tanh (a hyperbolic tangent) function for illustrative purposes – it is not a measurement of a real loudspeaker driver’s behaviour.
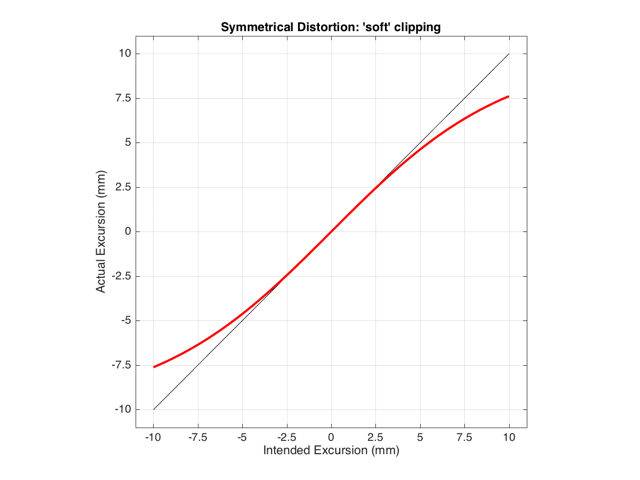
If we were to pass a sinusoidal waveform through this system, the result would be as is shown in Figure 6.
Harmonic Distortion
The reason engineers love sinusoidal waveforms is that they only contain one frequency each. A 1000 Hz sine tone only has energy at 1000 Hz and no where else. This means that if you have a box that does something to audio, and you put a 1000 Hz sine tone into it, and a signal with frequencies other than 1000 Hz comes out, then the box is distorting your sine wave in some way.
This was a very general statement and should be taken with a grain of salt. A gain applied perfectly to a signal is also a distortion (since the output is different from the input), but will not necessarily add new frequency components (and therefore it is linear distortion, not non-linear distortion). A box that adds noise to the signal is, generally speaking, distorting the input – but the output’s extra components are unrelated to the input – which would classify the problem as noise instead of distortion.) To be more accurate, I would have said that “if you have a box that does something to audio, and you put a 1000 Hz sine tone into it, and a signal with frequencies other than 1000 Hz comes out, then the box is applying a non-linear distortion to your sine wave in some way.”
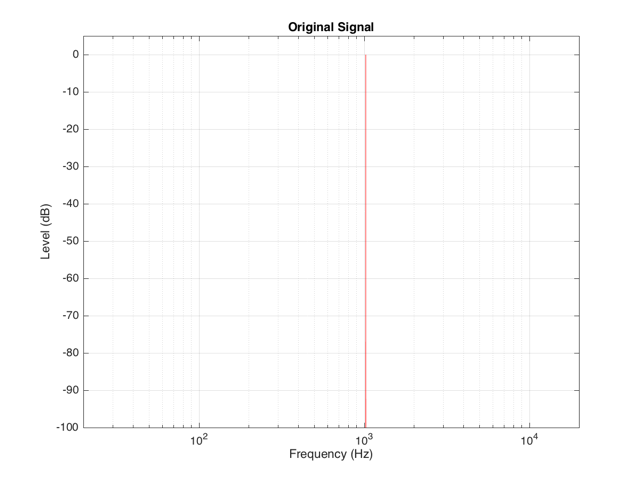
Back to the engineers… If you take a sinusoidal waveform and plot its frequency content, you’ll see something like Figure 7. This shows the frequency content of a signal consisting of a 1024 Hz sine wave.
If we clip this signal symmetrically, using the transfer function shown in Figure 1, resulting in the signal shown in the middle plot in Figure 2, and them measure the frequency content of the result, it will look like Figure 8.
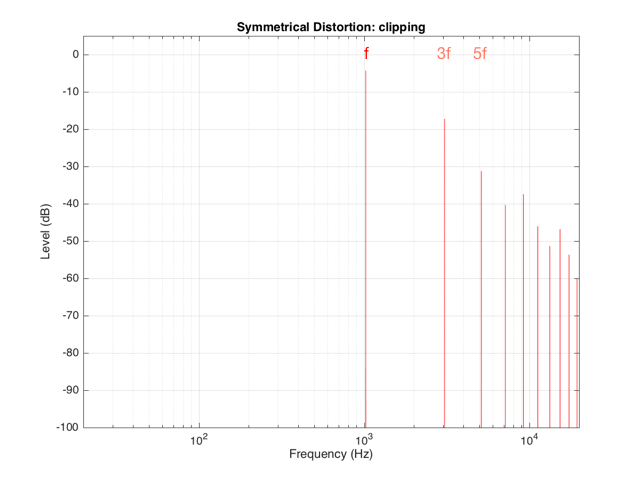
There are at least two interesting things to note about the frequency content shown in Figure 8.
The first is that the level of the signal at the fundamental frequency “f” (1024 Hz, in this case) is lower than the input. This might be obvious, since the output cannot “go as loud” as the input of the system – so some level is lost. (Since we’re clipping at -6 dB, the fundamental has dropped by 6 dB.)
The second thing to notice is that the new frequencies that have appeared are at odd multiples of the frequency of the original signal. So, we have content at 3072 Hz (3*1024), 5120 Hz (5*1024), 7168 Hz (7*1024) and so on. This is a characteristic of a symmetrically distorted signal (meaning not only that we have distorted the top and the bottom of the signal in the same way, but also that the signal itself was symmetrical to begin with). In other words, whenever you see a distortion product that only produces odd-order harmonics of the fundamental, you have a system that is distorting a symmetrical signal symmetrically.
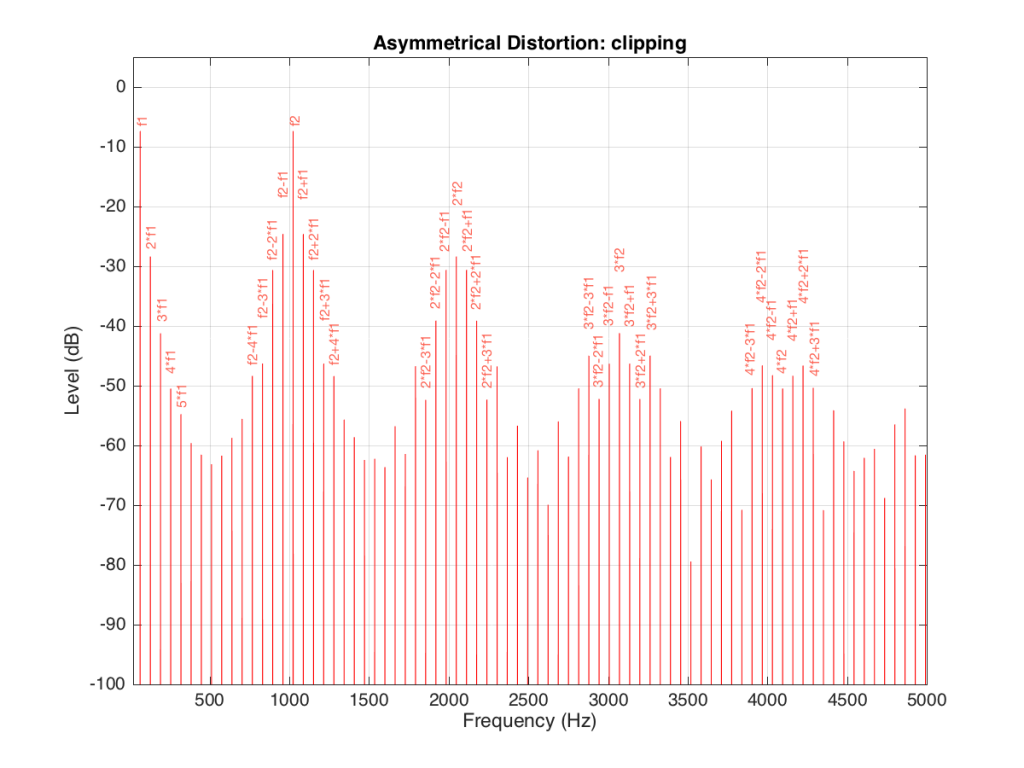
If we were to look at the frequency content of the asymmetrically-distorted signal (shown in Figures 3 and 4), the result would be as is shown in Figure 9.
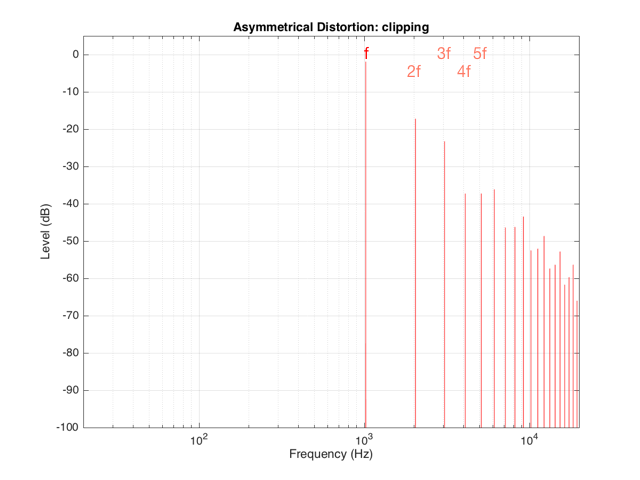
In Figure 9, you can see at least two interesting things:
The first is that the level of the fundamental frequency of “f” (1024 Hz) is higher than it was in Figure 8. This is because we’re letting more of the energy of the original waveform through the distortion (because the negative portion is untouched).
The second thing that you can see in Figure 9 is that both the odd-order and the even-order harmonics are showing up. So, we get energy at 2048 Hz (2*1024), 3072 Hz (3*1024), 4096 Hz (4*1024), 5120 Hz (5*1024), and so on. The presence of the even-order harmonics tells us that either the input signal was asymmetrical (which it wasn’t) or that the distortion applied to it was asymmetrical (which is was) or both.
If the distortion we apply to the signal was less abrupt – using the “soft-clipping” function shown in Figure 5 and 6, the result would be different, as is shown in Figure 10.
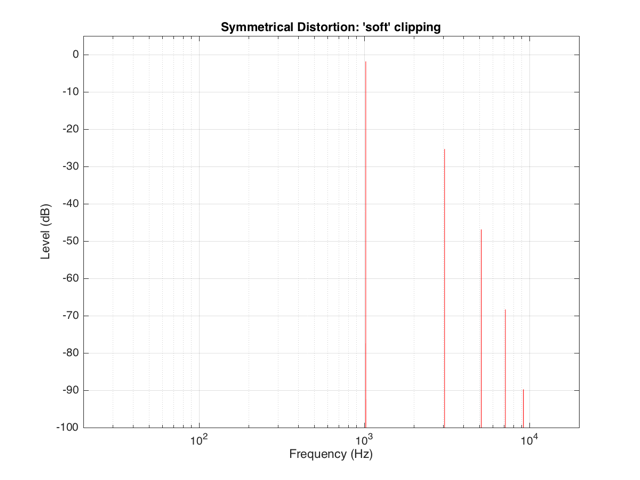
Again, in Figure 10, you can see that only the odd-order harmonics appear as the distortion products, since the distortion we’re applying to the symmetrical signal is symmetrical.
Intermodulation Distortion
So far, we’ve only been looking at the simple case of an input signal with a single frequency. Typically, however, research has shown that most persons listen to more than one frequency simultaneously (acoustical engineers and Stockhausen enthusiasts excepted…). So, let’s look at what happens when we have more than one frequency – say, two frequencies – in our input signal.
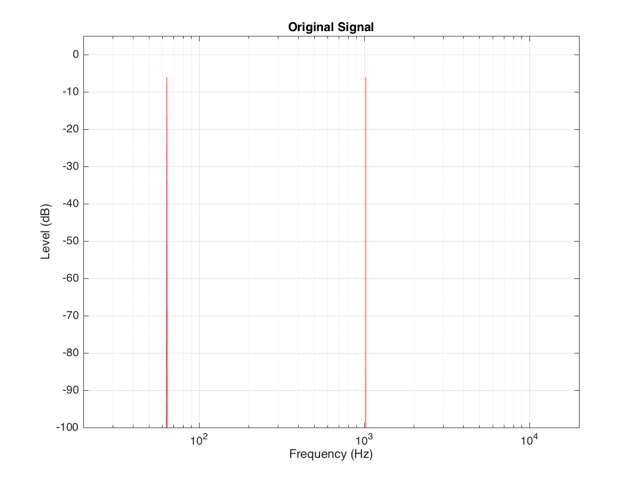
For example, let’s say that we have an input signal, the frequency content of which is shown in Figure 11, consisting of sinusoidal tones at 64 Hz and 1024 Hz. Both sine tones, individually, have a peak level of one-half of the maximum peak of the system. Therefore, they are shown in Figure 11 as having a level of approximately -6 dB each.
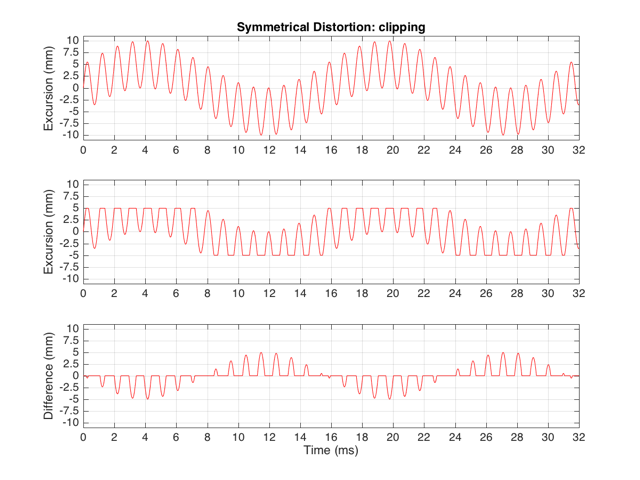
The sum of these two sinusoids will look like the top plot in Figure 12. As you can see there, the signal with the higher frequency is “riding on top of” the signal with the lower frequency. Each frequency, on its own, is pushing and pulling the excursion by ±5 mm. The total result therefore can move from -10 mm to +10 mm, but its instantaneous value is dependent on the overlap of the two signals at any one moment.
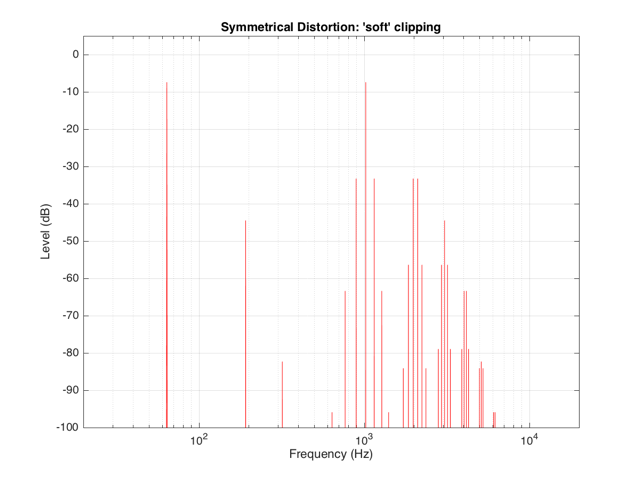
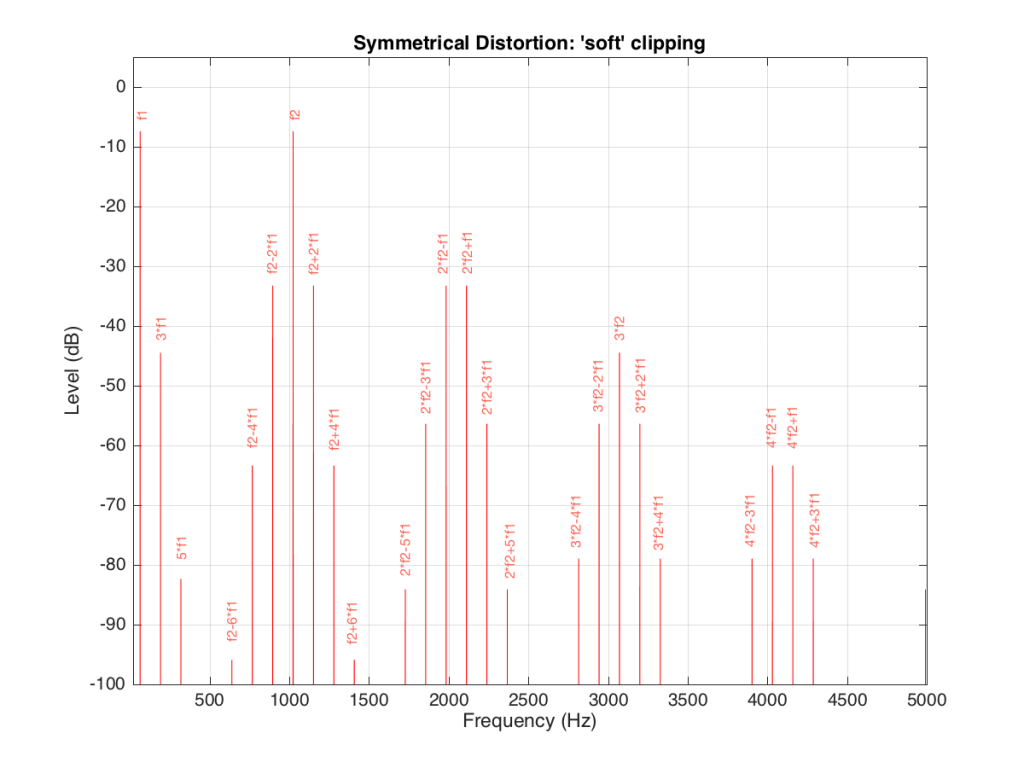
If we apply the symmetrical clipping shown in Figure 1 to this signal, the result is as is shown in the middle plot of Figure 12 (with the error shown in the bottom plot). This results in an interesting effect since, although the distortion we’re applying should be symmetrical, the result at any given moment is asymmetrical. This is because the signal itself is asymmetrical with respect to the clipping – the high frequency component alternates between getting clipped on the top and the bottom, depending on where the low frequency component has put it…
We can look at the frequency content of the resulting clipped signal. This is shown in Figure 13.
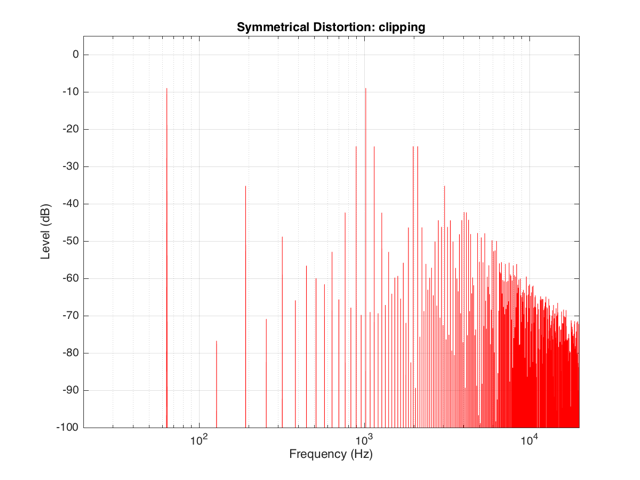
It’s obvious from the plot in Figure 13 that we have a mess. However, although the mess is rather systematic, it’s difficult to see in that plot. If we plot the same information on a different scale, things get easier to understand. Take a look at Figure 14.
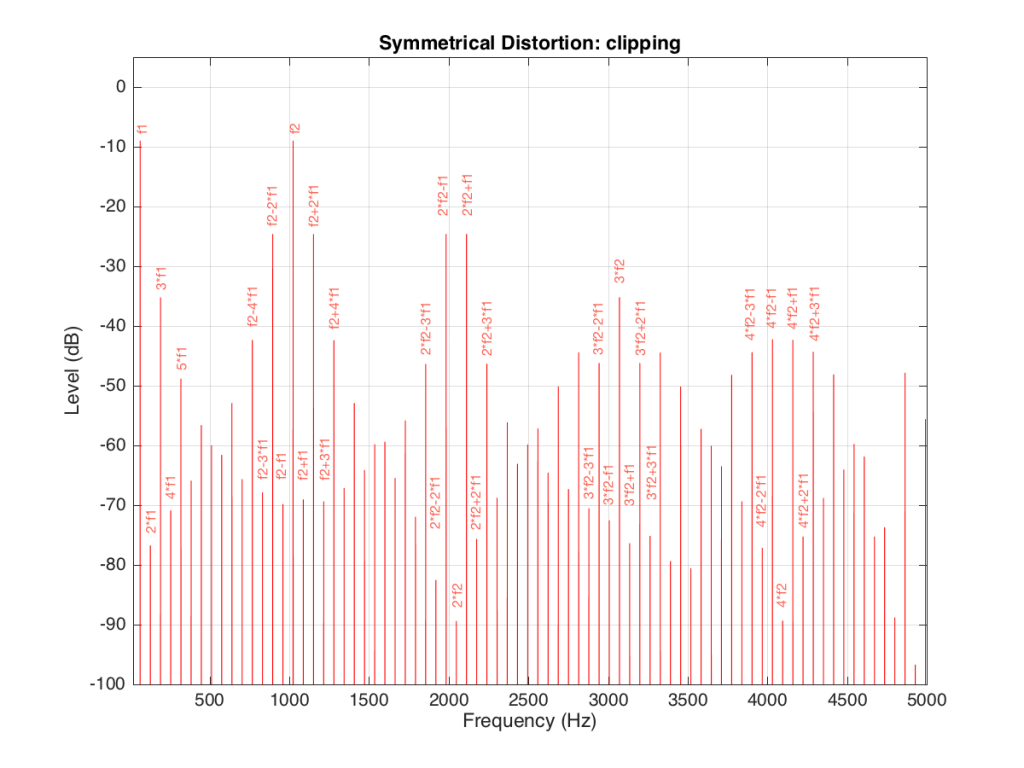
Figure 14 and Figure 13 show exactly the same information with only two differences. The first is that Figure 14 only shows frequencies up to 5 kHz instead of 20 kHz. The second is that the scale of the x-axis of Figure 13 is logarithmic whereas the scale of Figure 14 is linear. This is only a chance in spacing, but it makes things easier to understand.
As you can see in Figure 14, the extra frequencies added to the original signal by the clipping are regularly spaced. This is because the distortion that we have generated (called an intermodulation distortion, since it results from two two signals modulating each other), in the frequency domain, follows a pretty simple mathematical pattern.
Our original two frequencies of 64 Hz (called “f1” on the plot) and 1024 Hz (“f2”) are still present.
In addition, the sum and difference of these two frequencies are also present (f2+f1 = 1088 Hz and f2-f1 = 1018 Hz).
The sum and difference of the harmonic distortion products of the frequencies are also present. For example, 2*f2+f1 = 2*1024+64=2112 Hz, 3*fs-2*f1 = 3*1024-2*64 = 2944 Hz… There are many, many more of these. Take one frequency, multiply it by an integer and then add (or subtract) that from the other frequency multiplied by an integer – whatever the result, that frequency will be there. Don’t worry if your result is negative – that’s also in there (although we’re not going to talk about negative frequencies today – but trust me, they exist…)
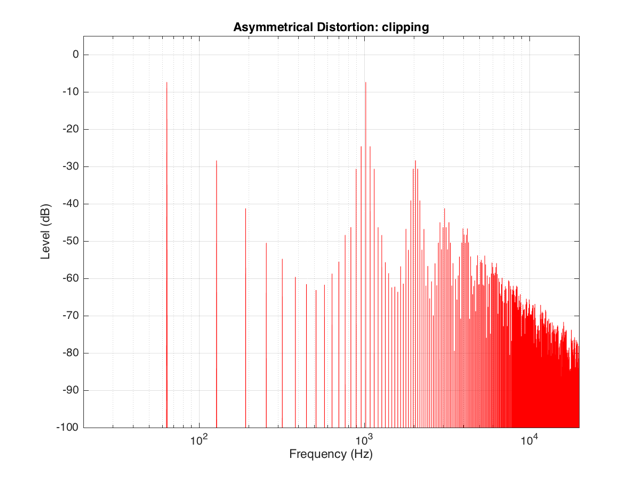
If we apply the asymmetrical clipping to the same signal, we (of course) get a different result, but it exhibits the same characteristics, just with different values, as can be seen in Figures 15 and 16.

Wrapping up
It’s important to state once more that none of the plots I’ve shown here are based on any real loudspeaker driver. I’m using simple examples of non-linear distortion just to illustrate the effects on an audio signal. The actual behaviour of an actual loudspeaker driver will be much more complicated than this, but also much more subtle (hopefully – if not, something it probably broken…).
Appendix
As I mentioned at the very beginning of this posting, many of the plots in this article have an intentional error. The reason I wrote this article is to try to give you an intuitive understanding of the results of a problem with the stiffness and Bl curves of a loudspeaker driver with respect to its excursion. This means that my plots of the time domain (such as those in Figure 2) show the excursion of the driver in millimetres with respect to time. I then skip over to a magnitude response plot, pretending that the signal that comes from a driver (a measurement of the air pressure) is identical to the pattern of the driver’s excursion. This is not true. The modulation in air pressure caused by a moving loudspeaker driver are actually in phase with the acceleration of the loudspeaker driver – not its excursion. So, I skipped a step or two. However, since I wasn’t actually showing real responses from real drivers, I didn’t feel too guilty about this. Just be warned that, if you’re really digging into this, you should not directly jump from loudspeaker driver excursion to a plot of the sound pressure.
B&O at Munich High-End
I’m on my way home from the Munich High End audio show where we were running continuous demos of the Beolab 90’s (an 8’45” mix of tracks on repeat from 10:00 a.m. to 6:00 p.m. for 4 days… It will be a while before I get the Chris Jones, Lyle Lovett and the Foo Fighters out of my head…)
We used an intentionally bare room – one Oppo Blu-ray player playing the .wav file off a USB stick, connected via S/P-DIF to the Beolab 90’s. Nothing else was in the room except three chairs, a lamp, and the people. The floor was carpeted, the ceiling was absorptive, and the walls were EXTREMELY reflective. (This helped people to hear the difference between Narrow and Wide mode – an intentional decision on my part… The room looks like a cell for someone in a straight jacket, but the listeners didn’t mind… In fact, many came back for a second listening session after hearing some of the other loudspeakers at the show…)


We spent a while the day before the show doing the Active Room Compensation measurements, and that was it – we were good to go!
The outside of the booth was simple – but the tree of Scan Speak drivers certainly attracted attention – audiophiles like drivers, apparently. :-)

Although it was nice to get out of the listening room in Struer for a while and meet some normal people – after four days on a 8’45” loop, it’s time to head home and listen to nothing for a day or two. :-)
B&O Tech: Location, Location, Location
#52 in a series of articles about the technology behind Bang & Olufsen loudspeakers
I often have to do demos of loudspeakers for people. Also, I frequently have to make recommendations on how to do (either for Bang & Olufsen dealers, or for things like press events). One of the problems that I face every time I have to do this is how to arrange the chairs so that everyone gets a reasonable impression of how a loudspeaker sounds. The problem is that this is basically impossible, due to the significant influence things like the loudspeakers’ locations, the listener location, and the room, have on the overall sound.
One aspect of how-a-loudspeaker-sounds is its magnitude response (often called a “frequency response”). A (perhaps too-simple) definition of a magnitude response is “a measure of how loud the output signal is at different frequencies if you put in a signal that is the same level at all frequencies”.
If we wanted to make a measurement of a loudspeaker’s magnitude response in a room at a particular position, we just have to put in a signal that contains all frequencies at the same magnitude (or level), capture that output with a microphone somewhere in the room, and compare how loud the signal is at different frequencies. Of course, in order to do this, we have to take care of some details. We have to make sure that the microphone (and everything else in the measurement part of the signal path) has a flat magnitude response. If it doesn’t, then at least we should know what its response is, so we can subtract it from the measurement to remove its influence on the result.
However, for the purposes of this posting, I’m not really interested in the absolute response of a loudspeaker. I’m more interested in how that response changes as you move in a room. Specifically, I want to show how much the magnitude response can change with very small changes in listening position.
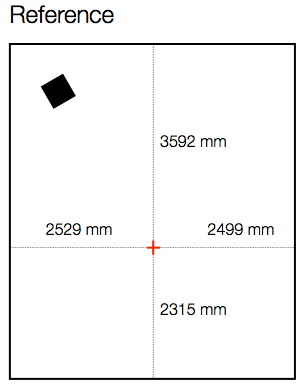
Let’s start by measuring the magnitude response of a loudspeaker in a room at a location. For the purposes of this example, I’ve used a full-range, multi-way loudspeaker without a port. It’s placed roughly 1 m from the side wall and 1 m from the front wall, aimed at a listening position. The listening position is in the centre of the room’s width, and closer to the rear wall than the front wall by about a metre. The details of the location for the microphone (a 1/4″ omnidirectional measurement mic) for this measurement are shown in Figure 1, below.
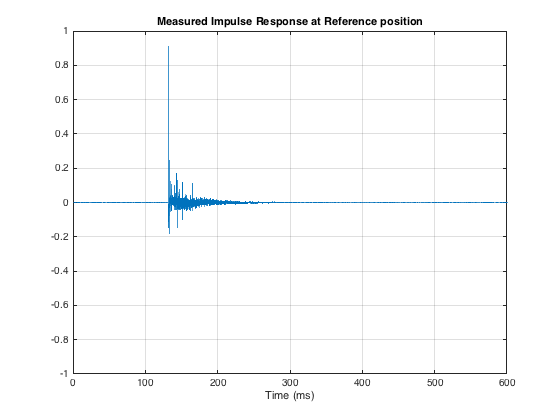
I did an impulse response measurement (using an MLS signal with 4 averages (to improve SNR) and 4 sequences (to reduce the effect of distortion)) of the loudspeaker, the result of which is shown below in Figure 2. As you can see there, there are many obvious reflections after the initial impulse, and there is some kind of ringing in the room’s response.
The extremely long time before the onset of the impulse is arbitrary. The microphone was not actually 40 m away from the loudspeaker…
As I said above, I’m not interested in the resulting magnitude response of this measurement. I can tell you that it’s messy. There are bumps and dips in the low end caused (primarily) by room modes. The top end is messy due to the reflections. The overall curve is not flat due to the loudspeaker’s response, the microphone’s orientation, and various components in the signal path. However, I don’t care, since I’m not here to measure how the speaker behaves at one location in the room. I’m here to find out how its behaviour changes when you change location. So, let’s move the microphone.
As you can see in Figure 3, below, I started by moving the microphone only 100 mm, directly forwards in the room.
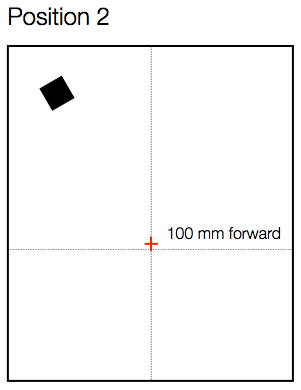
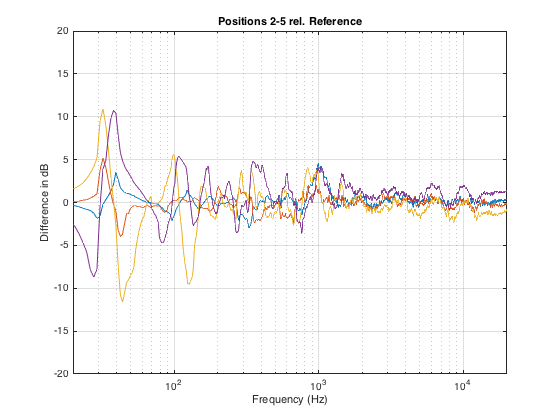
Again, I measured the impulse response, converted that to a magnitude response (reflections and all!), smoothed it with a running 1/3 octave smoothing and subtracted the magnitude response measured at the Reference position (also smoothed to 1/3 octave). The resulting difference is shown in Figure 4, below.
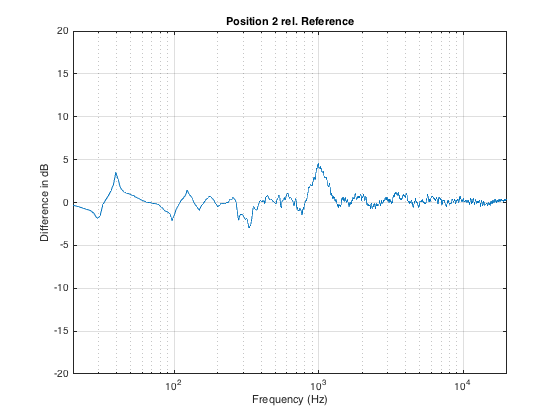
As you can see in Figure 3, moving the listening position only 100 mm results in a magnitude response deviation of about -2 to +4 dB. This is easily within the threshold of audibility for most people…
Now, let’s move the microphone sideways instead, as shown in Figure 5.
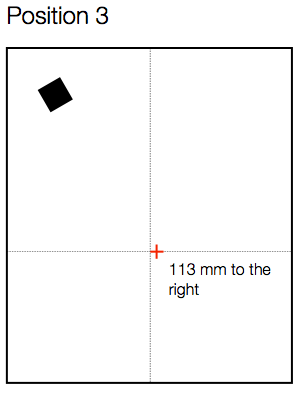
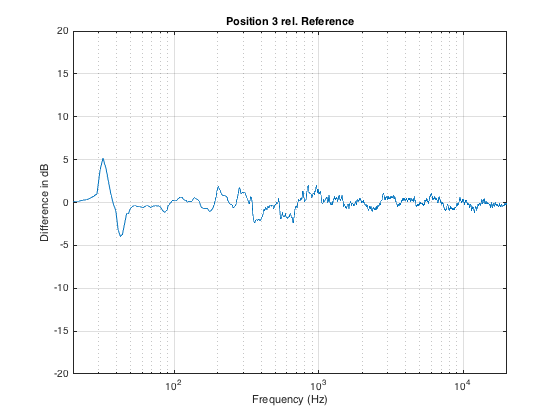
Again, a roughly 100 mm movement results in a large change in the magnitude response – although now the most significant changes have happened in the low end, as can be seen in Figure 6.
If we have more than one listener attending the demo, then I prefer to seat them “bus” style – one directly in front of the other – to ensure that everyone is getting a reasonably good phantom centre image. Sitting off-centre results in the time of arrival of signals from the two loudspeakers being mis-matched which will result in phantom images pulling towards the closer (and therefore earlier) loudspeaker.
Let’s say the we have a person roughly a half-metre behind the “good” chair, as shown in Figure 7. How different is the sound in that location?
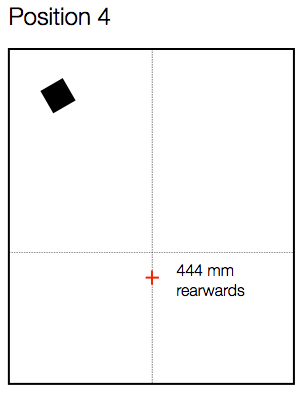
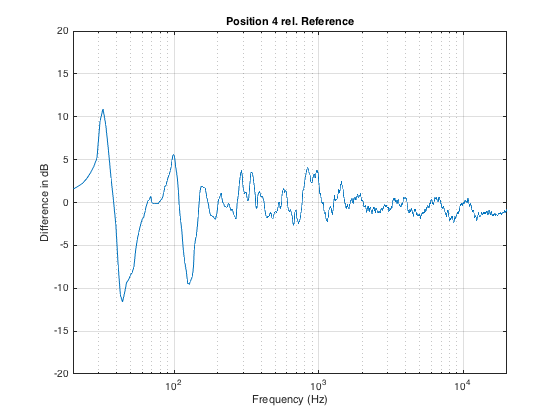
Now we can see in Figure 8 that, by moving backwards in the room, we get more than ± 10 dB of variation in the magnitude response, with significant deviations happening as high as 1 kHz (depending on how you define “significant”).
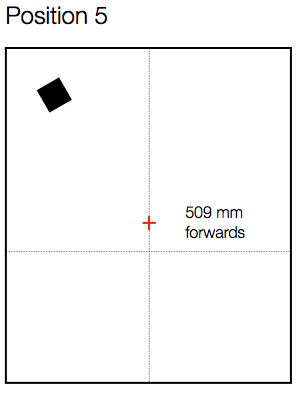
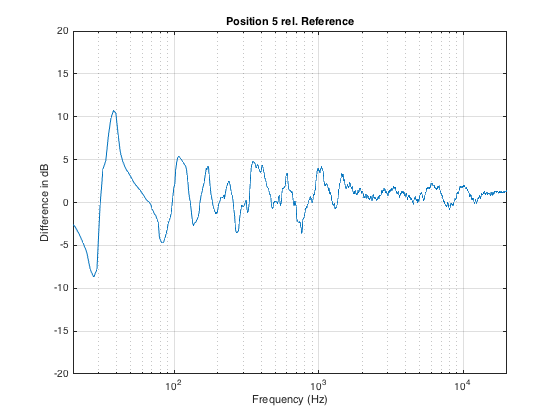
Similarly, moving forwards by a half metre from the Reference position (shown in Figure 9) results in a similar amount of change in the magnitude response, shown in Figure 10.
Just for comparison, I’ve re-plotted the 4 magnitude response differences shown above in one plot. This is to show that the changes are not necessarily easily predicable with a simple knowledge of room layout. In other words, it would be almost impossible, without some serious simulation software, to predict these changes just by looking at a floorplan of the room and the chairs.
What’s the moral of the story here? There are many – but I’ll just mention three.
The first is the message that, even a very small change in location (like leaning to one side in your chair – or leaning forwards to rest your elbows on your knees and your chin on your hands) can dramatically change the simple magnitude response of a loudspeaker (we won’t get into the effects on the spatial behaviour of the system).
The second is that, when you’re sitting with a friend, auditioning a pair of loudspeakers, switch chairs now and again. It is extremely unlikely that you’re both hearing the same thing at the same time.
Thirdly, the fact that there are significant differences between magnitude responses at different listening positions (even within a half-metre radius) means that, if you’re doing measurements for a room compensation system using a microphone around the listening position, it’s always smarter to make more than one measurement. In fact, there are some people who argue that, in this case, having only one measurement is worse than having no measurements, since you can easily get distracted by something in the magnitude or the time response that is a problem at only that location and nowhere else.
Finally, it’s worth considering that first point a different way. Let’s say you’re the type of person who likes to tweak a stereo system by upgrading components like wires. And, let’s say that you have incredible powers of “sonic memory” – in other words, you can listen to a system, take a break, listen to it again, and you are able to detect extremely small changes in system performance (like the magnitude response). So, you listen to your system – then you get out of your chair, change the component, sit down again, and start listening to the same tune at the same level. Remember that, unless you are in exactly the same location that you were before (not just “in the same chair”…), it could be that there is a larger difference in the magnitude response of the loudspeaker due your change in position than there is due to the component you just changed… So if you are a tweaker – get someone else to do the dirty work for you so you can sit there, in your chair, with your head in a clamp, waiting to evaluate the “upgrade”…
B&O Tech: The Cube
#51 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Sometimes, we have journalists visiting Bang & Olufsen in Struer to see our facilities. Of course, any visit to Struer means a visit to The Cube – our room where we do almost all of the measurements of the acoustical behaviour of our loudspeaker prototypes. Different people ask different questions about that room – but there are two that come up again and again:
- Why is the room so big?
- Why isn’t it an anechoic chamber?
Of course, the level of detail of the answer is different for different groups of people (technical journalists from audio magazines get a different level of answer than lifestyle journalists from interior design magazines). In this article, I’ll give an even more thorough answer than the one the geeks get. :-)
Introduction #1 – What do we want?
Our goal, when we measure a loudspeaker, is to find out something about its behaviour in the absence of a room. If we measured the loudspeaker in a “real” room, the measurement would be “infected” by the characteristics of the room itself. Since everyone’s room is different, we need to remove that part of the equation and try to measure how the loudspeaker would behave without any walls, ceiling or floor to disturb it.
So, this means (conceptually, at least) that we want to measure the loudspeaker when it’s floating in space.
Introduction #2 – What kind of measurements do we do?
Basically, the measurements that we perform on a loudspeaker can be boiled down into four types:
- on-axis frequency response
- off-axis frequency responses
- directivity
- power response
Luckily, if you’re just a wee bit clever (and we think that we are…), all four of these measurements can be done using the same basic underlying technique.
The very basic idea of doing any audio measurement is that you have some thing whose characteristics you’re trying to measure – the problem is that this thing is usually a link in a chain of things – but you’re only really interested in that one link. In our case, the things in the audio chain are electrical (like the DAC, microphone preamplifier, and ADC) and acoustical (like the measurement microphone and the room itself).
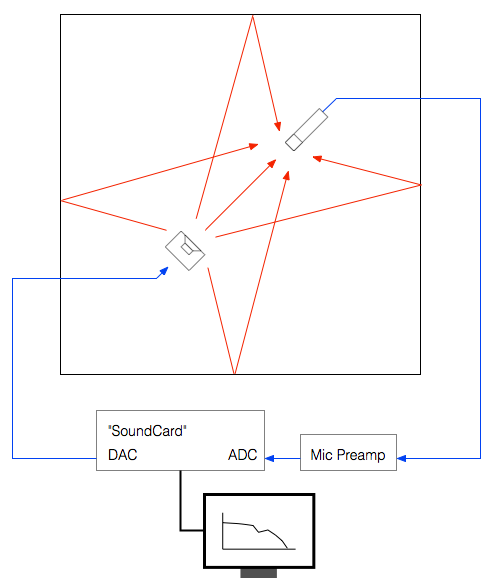
The computer sends a special signal (we’ll come back to that…) out of its “sound card” to the input of the loudspeaker. The sound comes out of the loudspeaker and comes into the microphone (however, so do all the reflections from the walls, ceiling and floor of the Cube). The output of the microphone gets amplified by a preamplifier and sent back into the computer. The computer then “looks at” the difference between the signal that it sent out and the signal that came back in. Since we already know the characteristics of the sound card, the microphone and the mic preamp, then the only thing remaining that caused the output and input signals to be different is the loudspeaker.
Introduction #3 – The signal
There are lots of different ways to measure an audio device. One particularly useful way is to analyse how it behaves when you send it a signal called an “impulse” – a click. The nice thing about a theoretically perfect click is that it contains all frequencies at the same amplitude and with a known phase relationship. If you send the impulse through a device that has an “imperfect” frequency response, then the click changes its shape. By doing some analysis using some 200-year old mathematical tricks (called “Fourier analysis“), we can convert the shape of the impulse into a plot of the magnitude and phase responses of the device.
So, we measure the way the device (in our case, a loudspeaker) responds to an impulse – in other words, its “impulse response”.
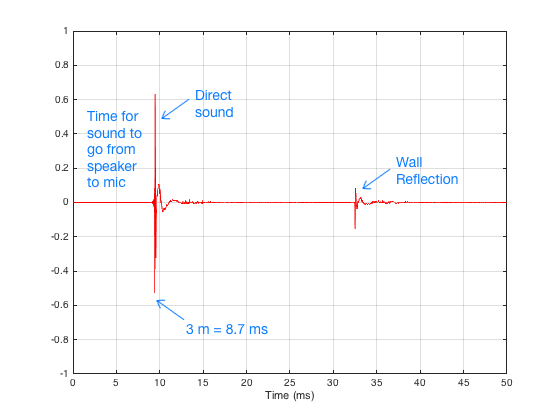
There are three things to initially notice in this figure.
- The first is the time before the first impulse comes in. This is the time it takes the sound to travel from the loudspeaker to the microphone. Since we normally make measurements at a distance of 3 m, this is about 8.7 ms.
- The second is the fact that the impulse doesn’t look perfect. That’s because it isn’t – the loudspeaker has made it different.
- The third is the presence of the wall reflection. (In real life, we see 6 of these – 4 walls, a ceiling and the floor – but this example is a simulation that I created, just to show the concept.)
In order to get a measurement of the loudspeaker in the absence of a room, we have to get rid of those reflections… In this case, all we have to do is to tell the computer to “stop listening” before that reflection arrives. The result is the impulse response of the loudspeaker in the absence of any reflections – which is exactly what we want.
- We make this measurement “on-axis” (usually directly in front of the loudspeaker, at some specific height which may or may not be the same height as the tweeter) to get a basic idea to begin with.
- We can then rotate the crane (the device hanging from the ceiling that the loudspeaker is resting on) with a precision of 1º. This allows us to make an off-axis measurement at any horizontal angle.
- In order to find the loudspeaker’s directivity (like Figure 5, 6, and 7 in this posting), we start by making a series of measurements (typically, every 5º for all 360º around the loudspeaker). We then tell the computer to compare the difference between each off-axis measurement and the on-axis measurement (because we’re only interested in how the sound changes with rotation – not its actual response at a given off-axis angle – we already got that in the previous measurement.
- Finally, we have to get the power response. This one is a little more tricky. The power response is the behaviour of the loudspeaker when measured in all directions simultaneously. Think of this as putting the loudspeaker in the centre of a sphere with a diameter of 3 m made of microphones. We send a signal out of the loudspeaker and measure the response at all points on the sphere, add them all together and see what the total is. This is an expensive way to do this measurement, since microphones cost a lot… An easier way is to use one microphone and rotate the loudspeaker (both horizontally and vertically) and do a LOT of off-axis measurements – not just rotating around the loudspeaker, but also going above and below it. We do each of these measurements individually, and then add the results to get a 3D sum of all responses in all directions. That total is the power response of the loudspeaker – a measurement of the total energy the loudspeaker radiates into the room.


The original questions…
Great. That’s a list of the basic measurements that come out of The Cube. However, I still have’t directly answered the original questions…
Let’s take the second question first: “Why isn’t The Cube an anechoic chamber?”
This raises the question: “What’s an anechoic chamber?” An anechoic chamber is a room whose walls are designed to be absorptive (typically to sound waves, although there are some chambers that are designed to absorb radio waves – these are for testing antennae instead of loudspeakers). If the walls are perfectly absorptive, then there are no reflections, and the loudspeaker behaves as if there are no walls.
So, this question has already been answered – albeit indirectly. We do an impulse response measurement of the loudspeaker, which is converted to magnitude and phase response measurements. As we saw in Figure 5, the reflections off the walls are easily visible in the impulse response. Since, after the impulse response measurement is done, we can “delete” the reflection (using a process called “windowing”) we end up with an impulse response that has no reflections. This is why we typically say that The Cube is “pseudo-anechoic” – the room is not anechoic, but we can modify the measurements after they’re done to be the same as if it were.
Now to the harder question to answer: “Why is the room so big?”
Let’s say that you have a device (for example, a loudspeaker), and it’s your job to measure its magnitude response. One typical way to do this is to measure its impulse response and to do a DFT (or FFT) on that to arrive at a magnitude response.
Let’s also say that you didn’t do your impulse response measurement in a REAL free field (a space where there are no reflections – the wave is free to keep going forever without hitting anything) – but, instead, that you did your measurement in a real space where there are some reflections. “No problem,” you say “I’ll just window out the reflections” (translation: “I’ll just cut the length of the impulse response so that I slice off the end before the first reflection shows up.”)
This is a common method of making a “pseudo-anechoic” measurement of a loudspeaker. You do the measurement in a space, and then slice off the end of the impulse response before you do an FFT to get a magnitude response.
Generally speaking, this procedure works fairly well… One thing that you have to worry about is a well-known relationship between the length of the impulse response (after you’ve sliced it) and the reliability of your measurement. The shorter the impulse response, the less you can trust the low-frequency result from your FFT. One reason for this is that, when you do an FFT, it uses a “slice” of time to convert the signal into a frequency response. In order to be able to measure a given frequency accurately, the FFT math needs at least one full cycle within the slice of time. Take a look at Figure 6, below.
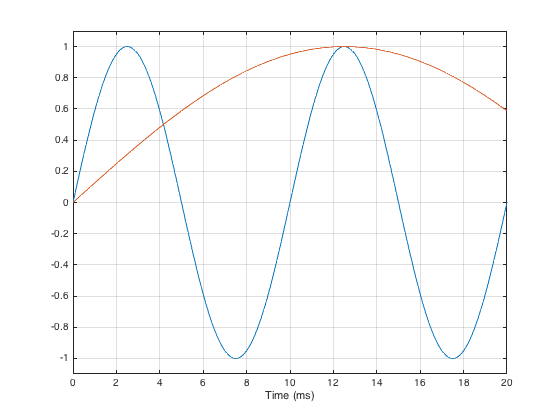
As you can see in that plot, if the slice of time that we’re looking at is 20 ms long, there is enough time to “see” two complete cycles of a 100 Hz sine tone (in blue). However, 20 ms is not long enough to see even one half of a cycle of a 20 Hz sine tone (in red).
However, there is something else to worry about – a less-well-known relationship between the level and extension of the low-frequency content of the device under test and the impulse response length. (Actually, these two issues are basically the same thing – we’re just playing with how low is “low”…)
Let’s start be inventing a loudspeaker that has a perfectly flat on-axis magnitude response but a low-frequency limitation with a roll-off at 10 Hz. I’ve simulated this very unrealistic loudspeaker by building a signal processing flow as shown in Figure 7.
If we were to do an impulse response measurement of that system, it would look like the plot in Figure 8, below.

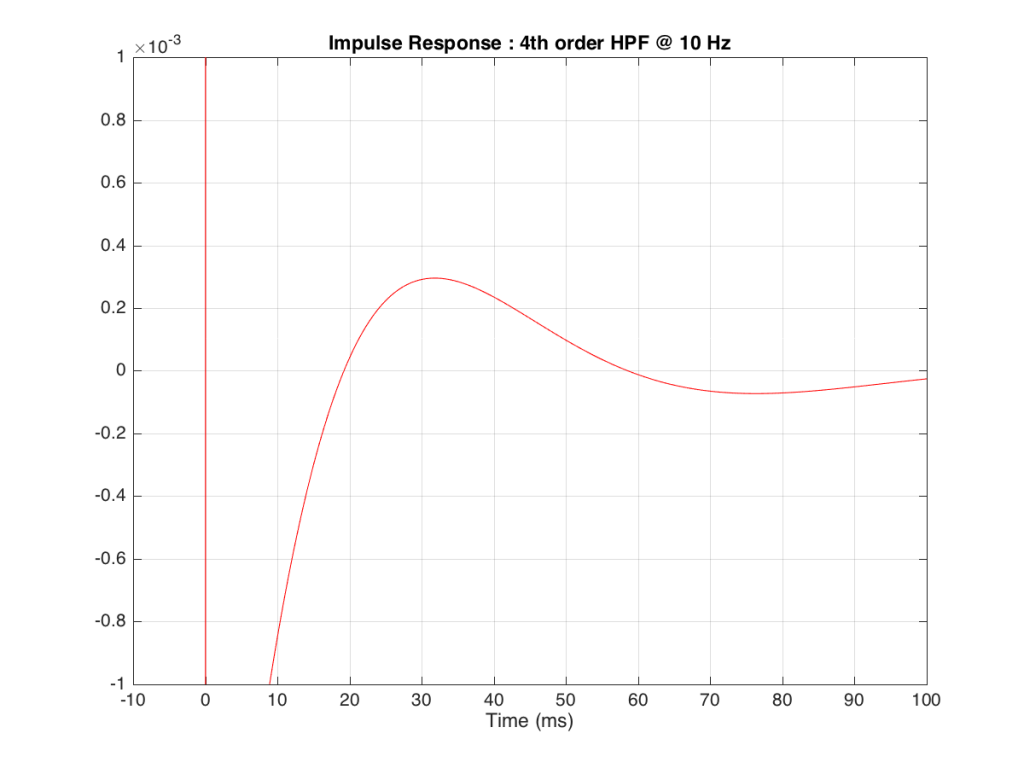
Figure 9, above shows a closeup of what happens just after the impulse. Notice that the signal drops below 0, then swings back up, then negative again. In fact, this keeps happening – the signal goes positive, negative, positive, negative – theoretically for an infinite amount of time – it never stops. (This is why the filters that I used to make this high pass are called “IIR” filters or “Infinite Impulse Response” filters.)
The problem is that this “ringing” in time (to infinity) is very small. However, it’s more easily visible if we plot it on a logarithmic scale, as shown below in Figure 10.
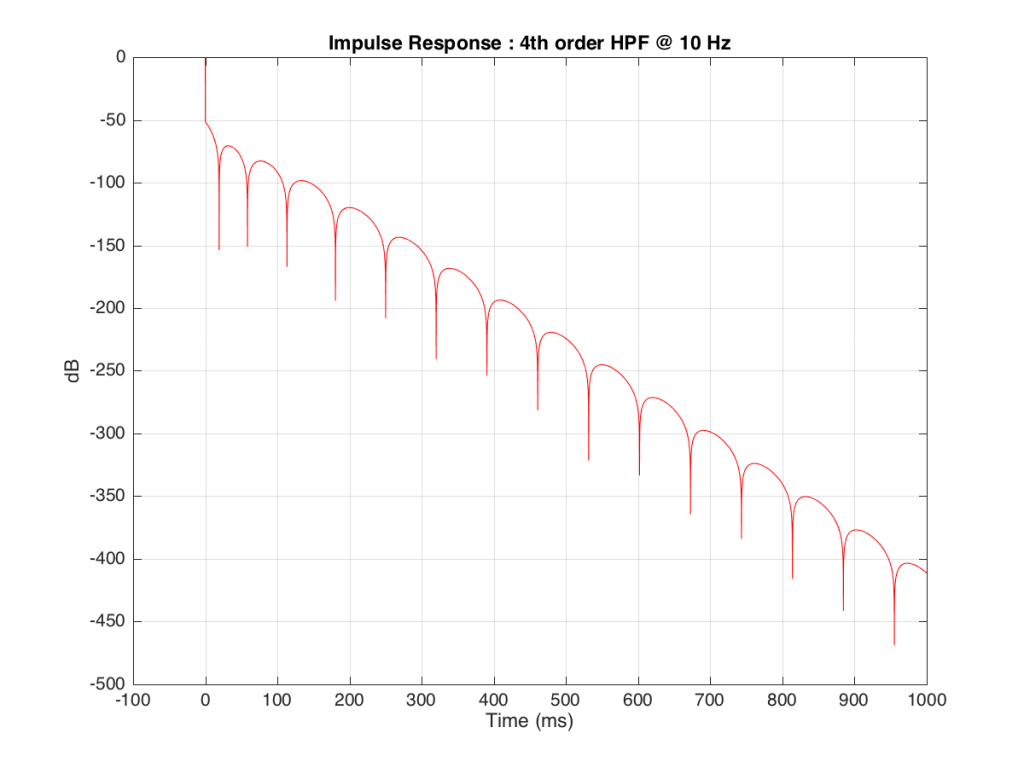
As you can see there, after 1 second (1000 ms) the oscillation caused by the filtering has dropped by about 400 dB relative to the initial impulse (that means it has a level of about 0.000 000 000 000 000 000 01 if the initial impulse has a value of 1). This is very small – but it exists. This means that, if we “cut off” the impulse to measure its frequency response, we’ll be cutting off some of the signal (the oscillation) and therefore getting some error in the conversion to frequency. The question then is: how much error is generated when we shorten the impulse length?
We won’t do an analysis of how to answer this question – I’ll just give some examples. Let’s take the total impulse response shown in Figure 6 and cut it to different lengths – 10, 15, 20, 25, 30 and 1000 ms. For each of those versions, I’ll take an FFT and look at the resulting magnitude response. These are shown below in Figure 11.
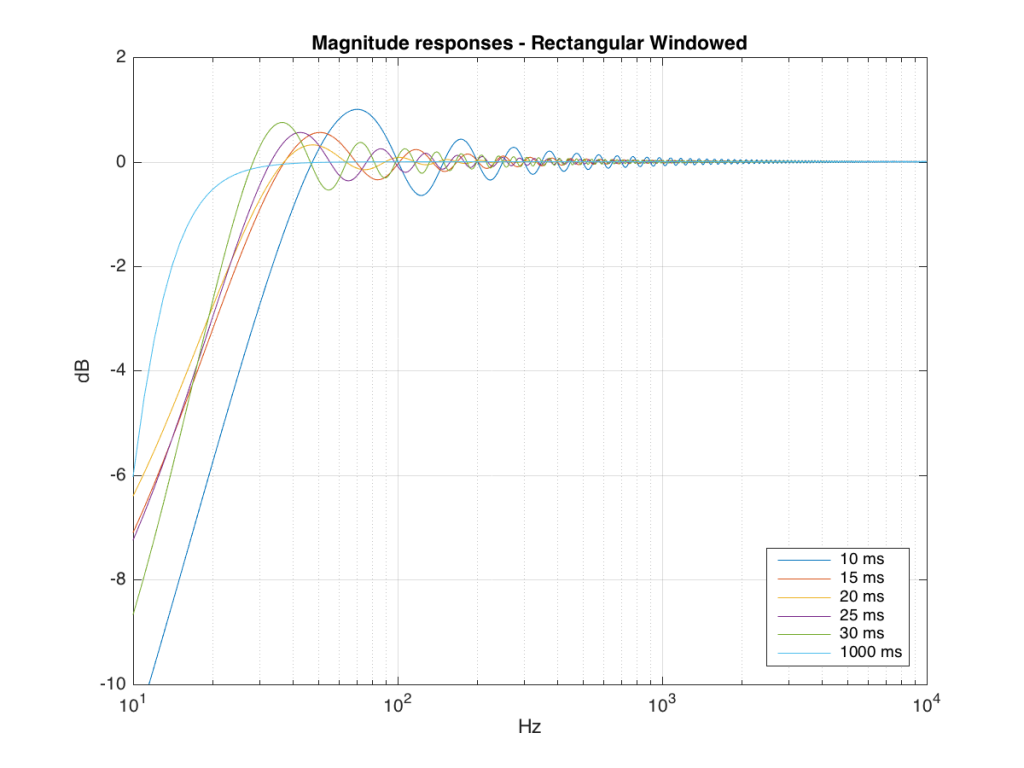
Figure 11: The magnitude responses resulting from taking an FFT of a shortened portion of a single impulse response plotted in Figure 8.
We’ll assume that the light blue curve in Figure 9 is the “reference” since, although it has some error due to the fact that the impulse response is “only” one second long, that error is very small. You can see in the dark blue curve that, by doing an FFT on only the first 10 ms of the total impulse response, we get a strange behaviour in the result. The first is that we’ve lost a lot in the low frequency region (notice that the dark blue curve is below the light blue curve at 10 Hz). We also see a strange bump at about 70 Hz – which is the beginning of a “ripple” in the magnitude response that goes all the way up into the high frequency region.
The amount of error that we get – and the specific details of how wrong it is – are dependent on the length of the portion of the impulse response that we use.
If we plot this as an error – how wrong is each of the curves relative to our reference, the result looks like Figure 12.
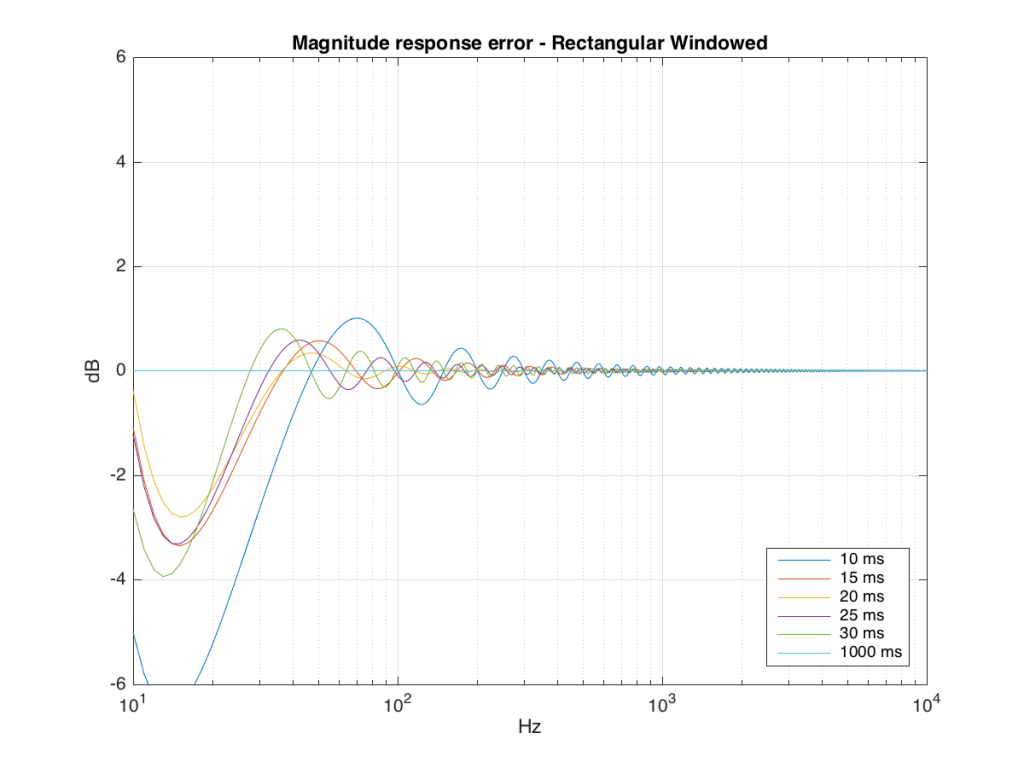
So what?
As you can see there, using a shorted impulse response produces an error in our measurement when the signal has a significant low frequency output. However, as we said above, we shorten the impulse response to delete the early reflections from the walls of The Cube in our measurement to make it “pseudo-anechoic”. This means, therefore, that we must have some error in our measurement. In fact, this is true – we do have some error in our measurement – but the error is smaller than it would have been if the room had been smaller. A bigger room means that we can have a longer impulse response which, in turn, means that we have a more accurate magnitude response measurement.
“So why not use an anechoic chamber and not mess around with this ‘pseudo-anechoic’ stuff?” I hear you cry… This is a good idea, in theory – however, in practice, the problem that we see above is caused by the fact that the loudspeaker has a low-frequency output. Making a room anechoic at a very low frequency (say, 10 Hz) would be very expensive AND it would have to be VERY big (because the absorptive wedges on the walls would have to be VERY deep – a good rule of thumb is that the wedges should be 1/4 of the wavelength of the lowest frequency you’re trying to absorb, and a 10 Hz wave has a wavelength of 34.4 m, so you’d need wedges about 8.6 m deep on all surfaces… This would therefore be a very big room…)
Appendix 1 – Tricks
Of course, there are some tricks that can be played to make the room seem bigger than it is. One trick that we use is to do our low-frequency measurements in the “near field” which is much closer than 3 m from the loudspeaker, as is shown in Figure 13 below. The advantage of doing this is that it makes the direct sound MUCH louder than the wall reflections (in addition to making the difference in their time of arrival at the microphone slightly longer) which reduces their impact on the measurement. The problem with doing near-field measurements is that you are very sensitive to distance – and you typically have to assume that the loudspeaker is radiating omnidirectional – but this is a fairly safe assumption in most cases.

Appendix 2 – Windowing
Those of you with some experience with FFT’s may have heard of something called a windowing function which is just a fact way to slice up the impulse response. Instead of either letting signal through or not, we can choose to “fade out” the impulse response more gradually. This changes the error that we’ll get, but we’ll still get an error, as can be seen below.
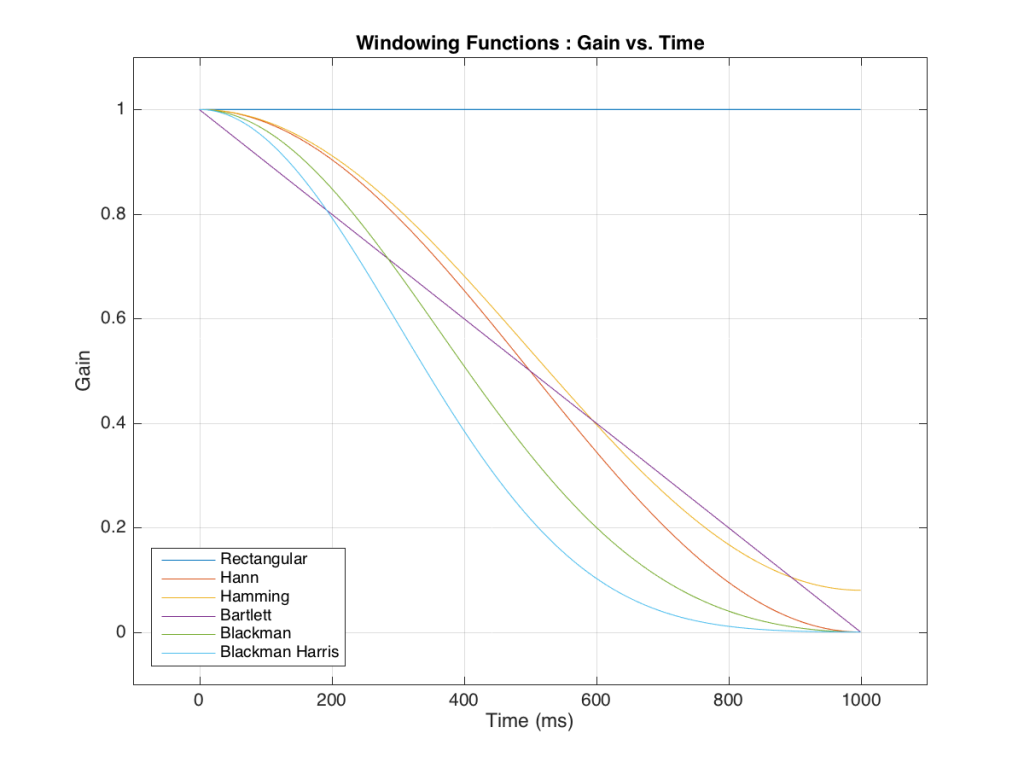
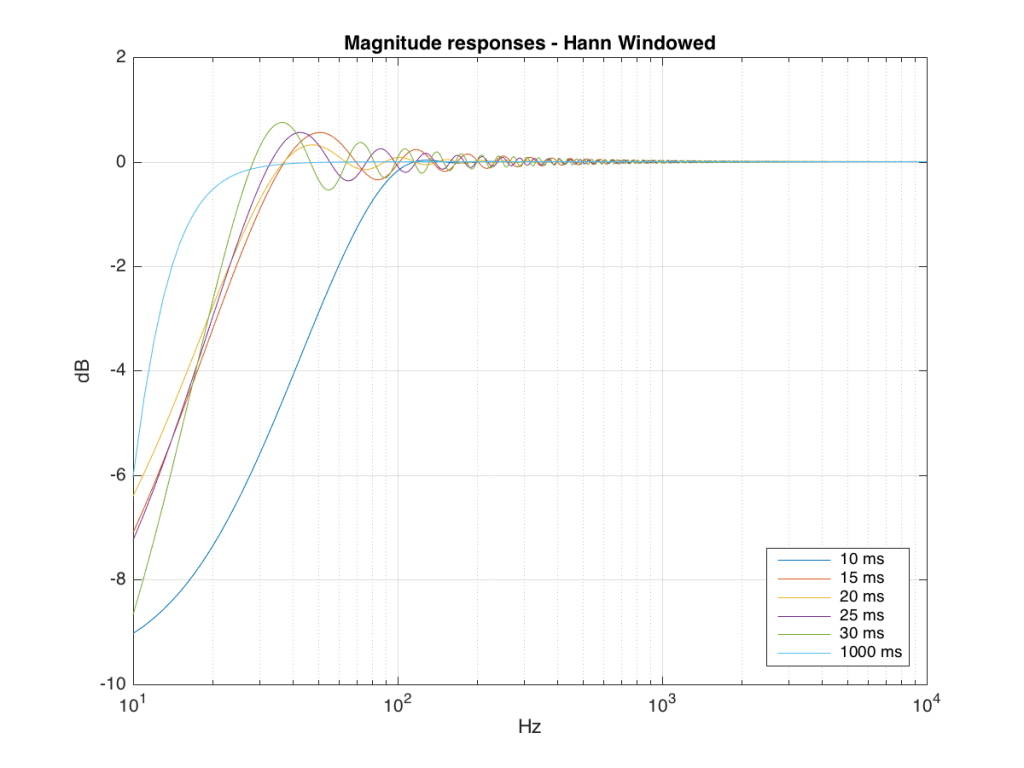
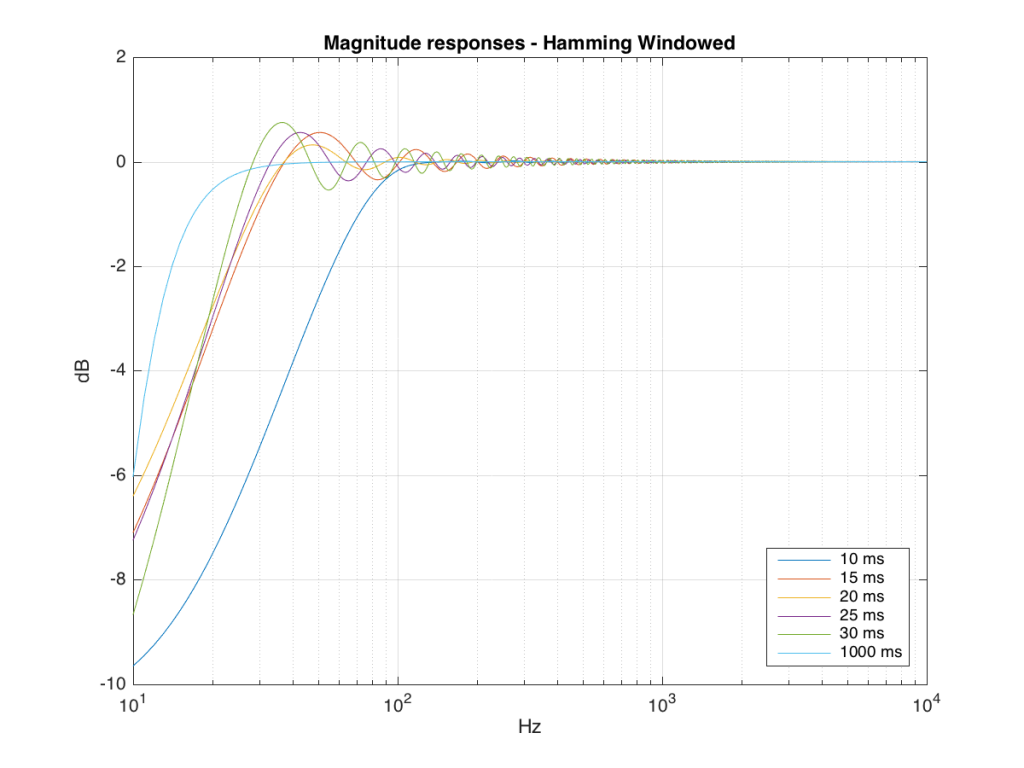
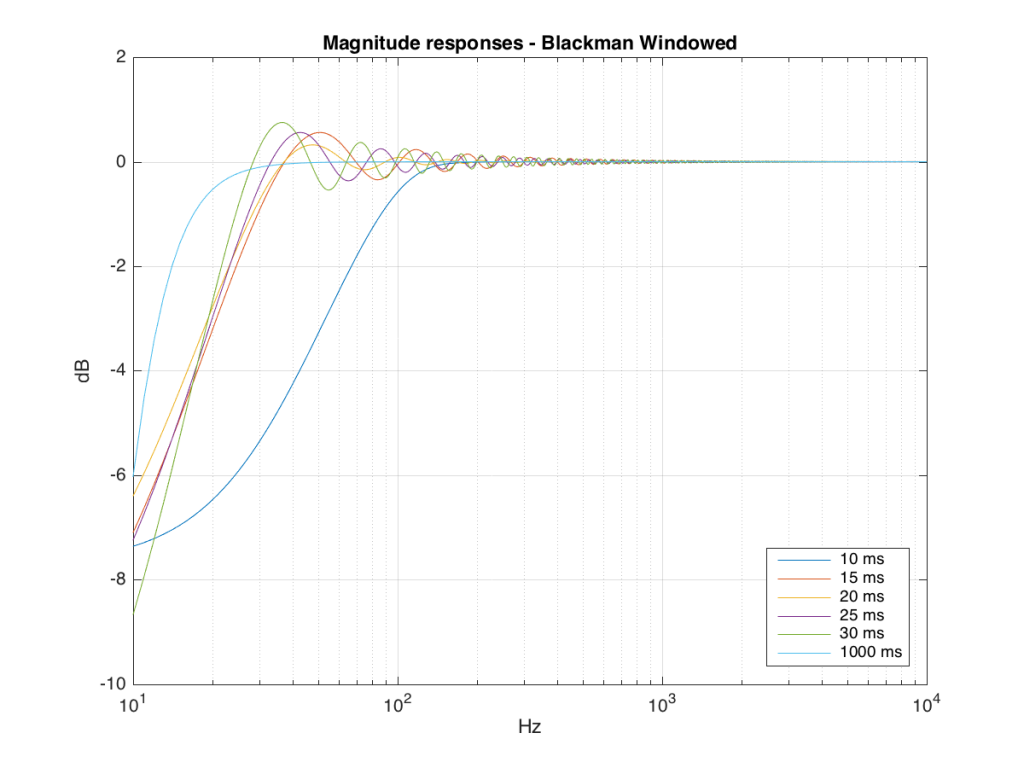
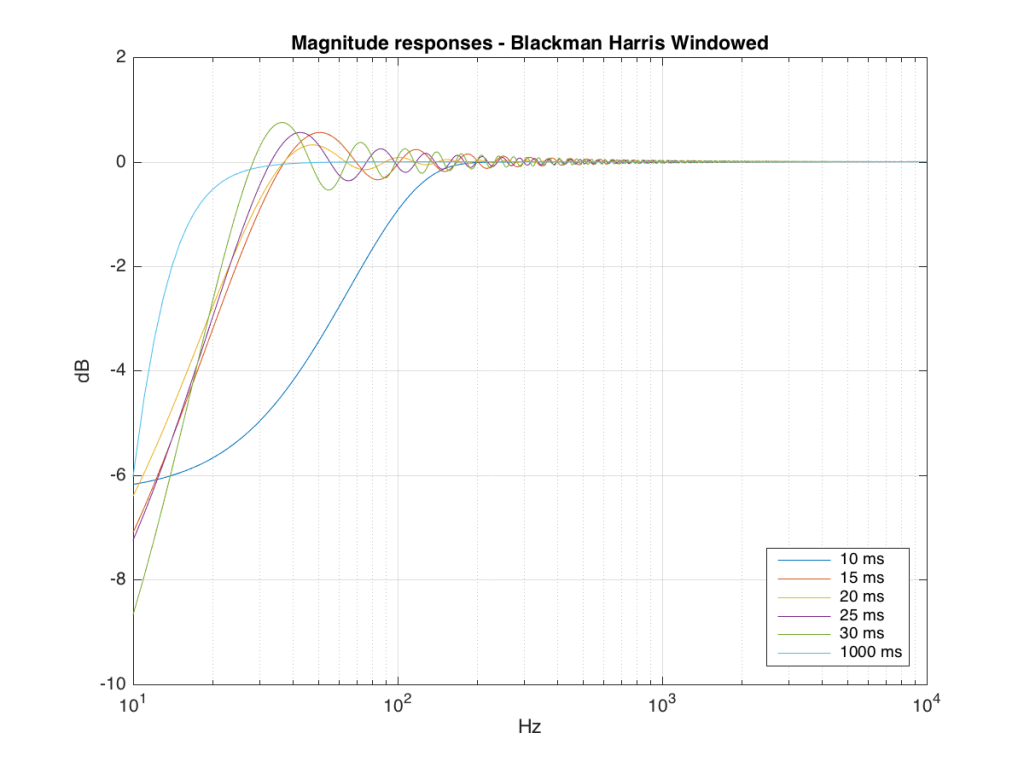
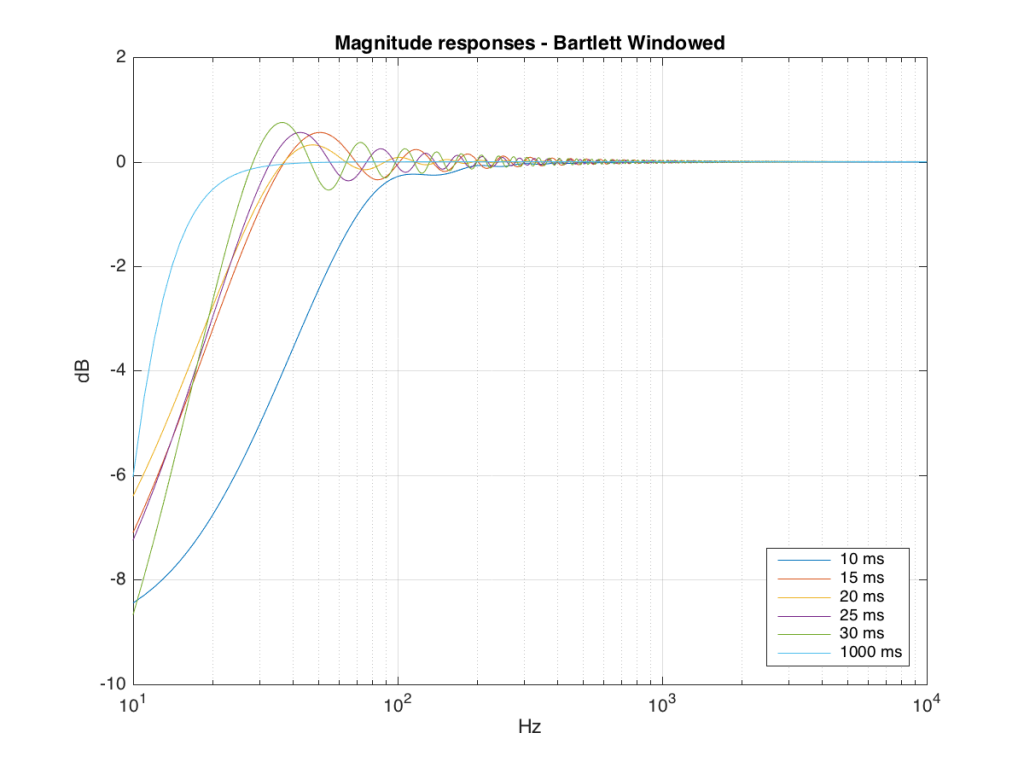
So, as you can see with all of those, the error is different for each windowing function and impulse response length – but there’s no “magic bullet” here that makes the problems go away. If you have a loudspeaker with low-frequency output, then you need a longer impulse response to see what it’s doing, even in the higher frequencies.
Pen Point Percussion