This is just a collection of information about turntables and vinyl for anyone wanting to dig deeper into It (which might mean that it’s just for me…). I’ll keep adding to this (and completing it) as time goes by.

Glossary

Cantilever

• The rod or arm that connects the stylus on one end to the “motor” on the other.

Effective Length

• The straight-line distance between the pivot point of the tonearm and the top of the stylus

Equivalent Mass

• definition to come

Flutter

• Higher-frequency modulation of the audio frequency caused by changes in the groove speed. These may be the result of changes in problems such as unstable motor speed, variable compliance on a belt, issues with a spindle bearing, drive wheel eccentricity, and other issues.
• Flutter describes a modulation in the groove speed ranging from 6 to 100 times a second (6 Hz to 100 Hz).

Frequency Drift

• Very long-term (or low-frequency) changes in the audio frequency, typically caused by slow changes in the platter rotation speed.
• Typically, changes with a modulation frequency of less than 0.5 Hz (a period of no less than 2 seconds) are considered to be frequency drift. Faster changes are labelled “Wow”

Groove

• The v-shaped track pressed into the surface of the vinyl record, in which the stylus sits

Linear Tracking

• A tonearm that moves linearly, following a path that is parallel to the radius line traced by the stylus. This (in theory) ensures that the tracking error is always 0º, however, in practice this error is merely small.

Modulation Width

• The distance measured on a line through the spindle from the start of the modulated groove to the end of the modulated groove. This is approximately 3″ or 76 mm.

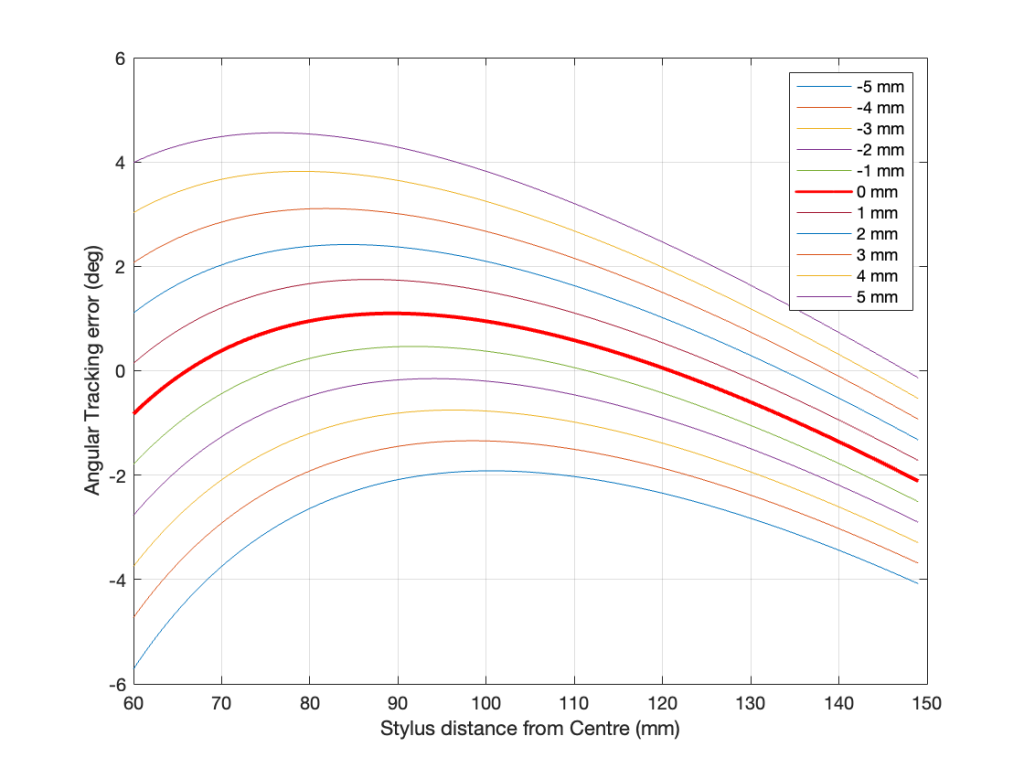
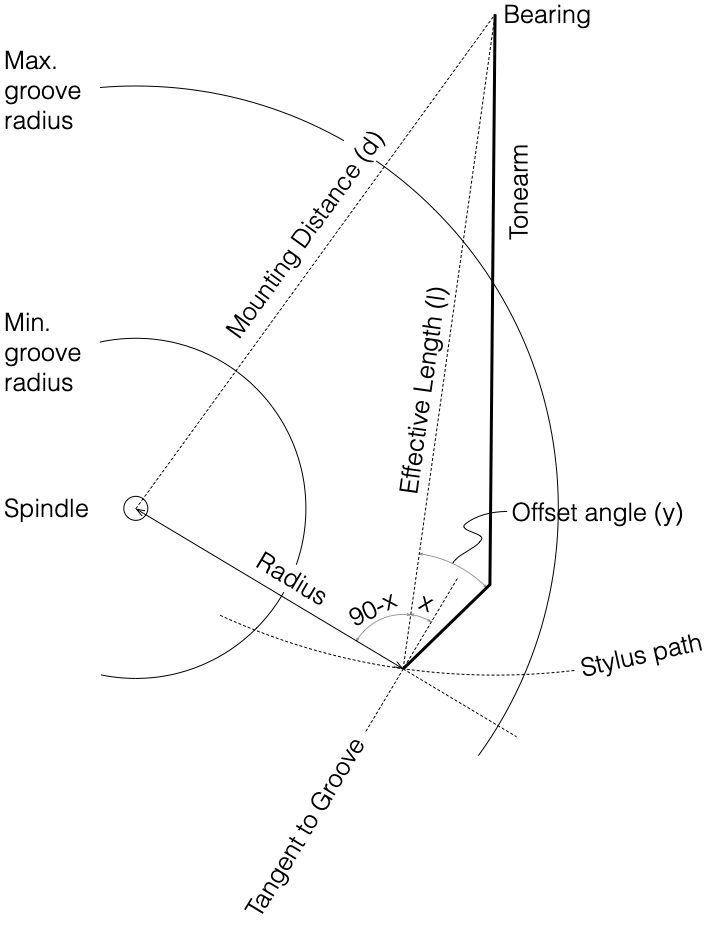
Mounting Distance

• The distance between the spindle and the pivot point of the tonearm.

Needle

• Also known as the stylus. The point that is placed in the groove of the vinyl record.
  Some persons distinguish between the “stylus” (to indicate the chisel on the mastering lathe that creates the groove in the master record), and the “needle” (to indicate the portion of the pickup on a turntable that plays the signal).

Null Radius

• The radius (distance between the spindle and the stylus) where the tracking error is 0º. A typically-designed and correctly installed radial tracking tonearm has two null radii (see this posting).

Offset Angle

• The angle between the axis of the stylus and a line drawn between the tonearm pivot and the stylus. See the line diagram below.

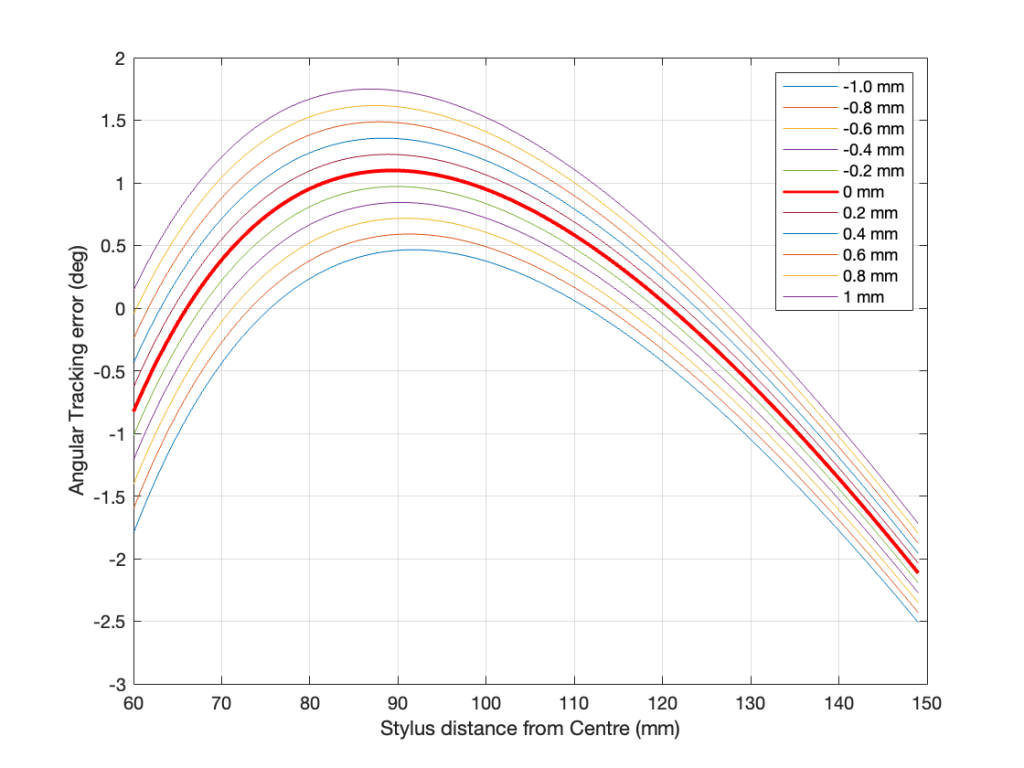
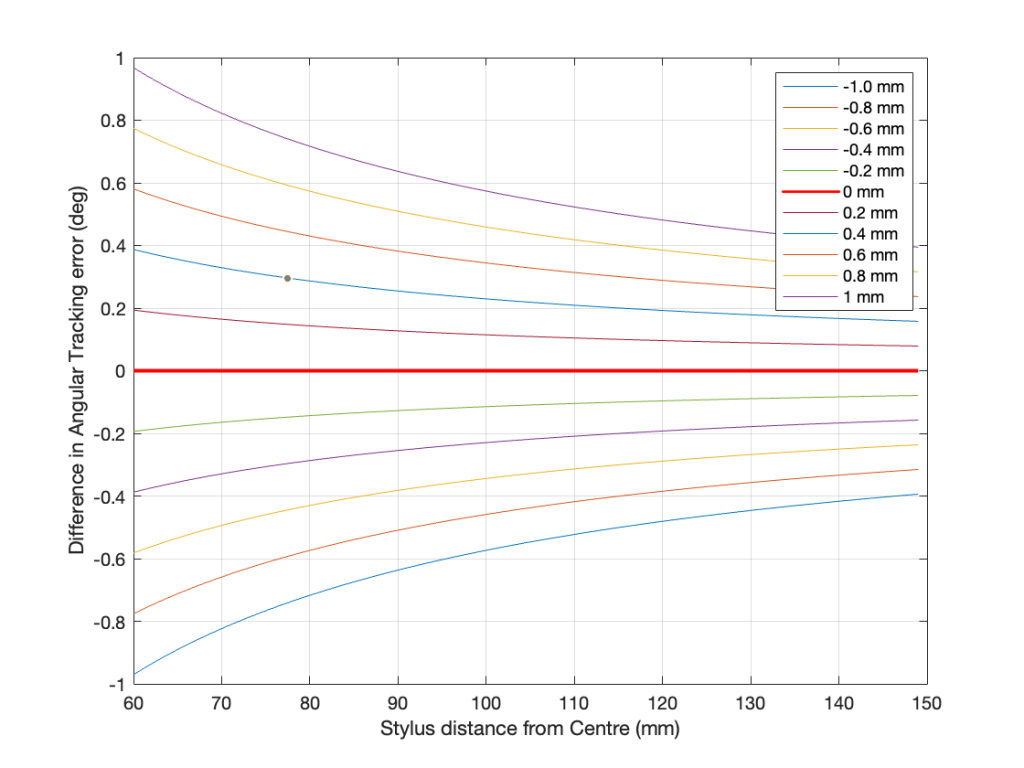
Overhang

• The difference between the Effective Length of the tonearm and the Mounting Distance. This value is used in some equations for calculating the Tracking Error.

Pickup, Electromagnetic

• Includes three general types: Moving Coil, Moving Magnet, and Variable Reluctance (aka Moving Iron). These produce an output proportional to the velocity of the stylus movement.

Pickup, Piezoelectic

• Produces an output proportional to the displacement of the stylus.

Pitch

• The density of the groove count per distance in lines per inch or lines per mm. The pitch can vary from disc to disc, or even within a single track, according to the requirements of the mastering.

Radial Tracking

• A tonearm that rotates on a pivot point with the stylus tracing a circular path around that pivot.

Radius

• The distance between the centre of the vinyl disc and the pickup stylus.

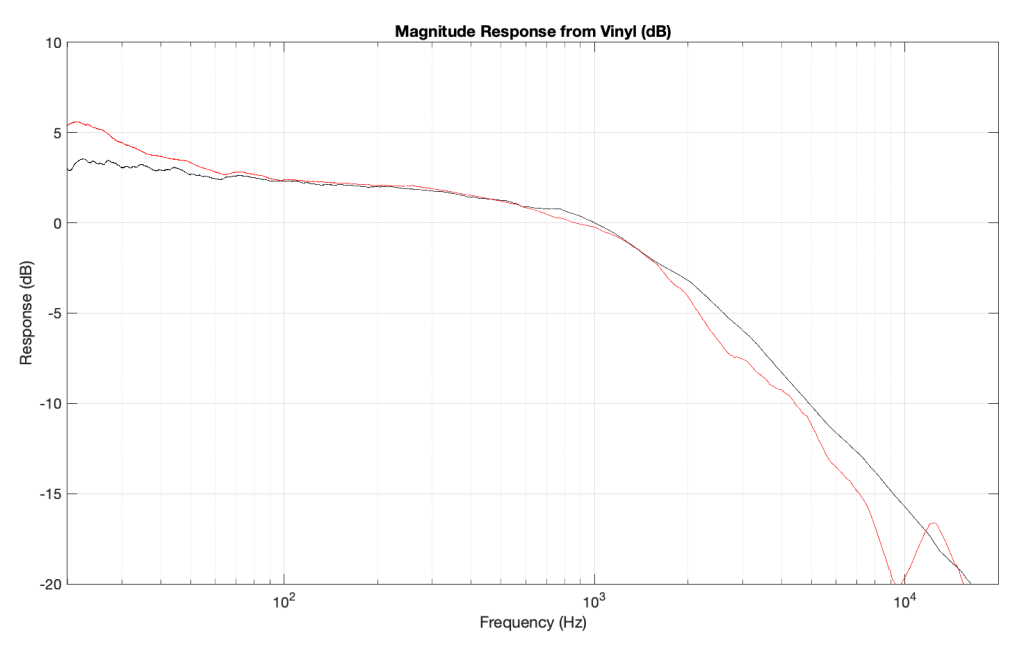
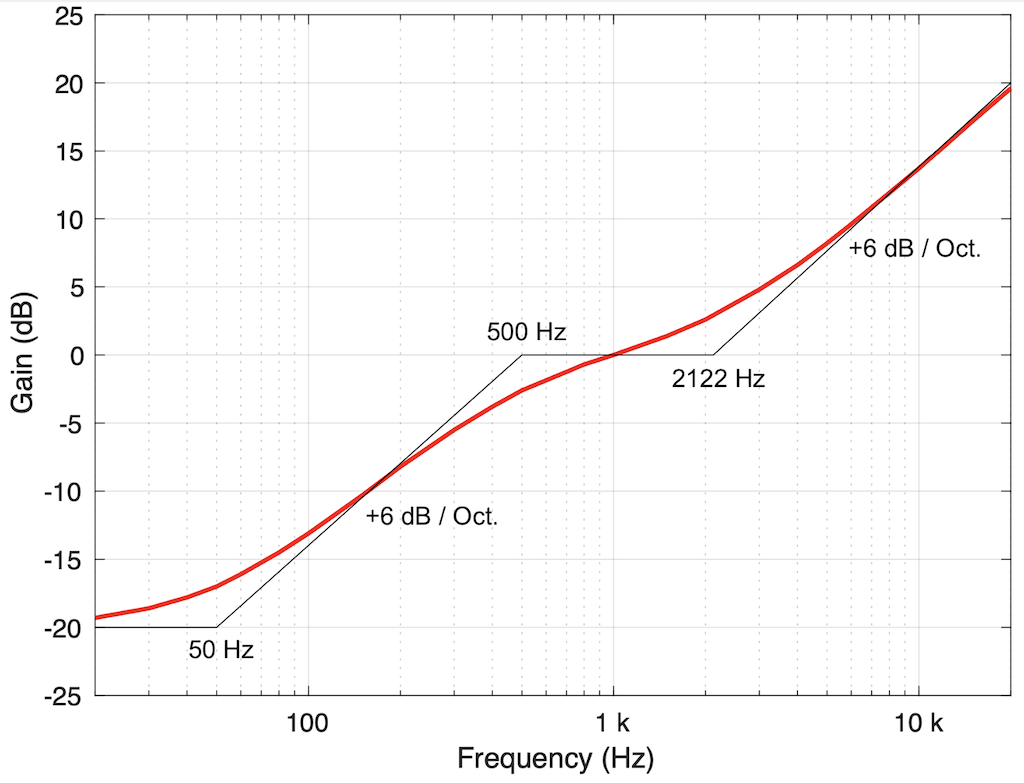
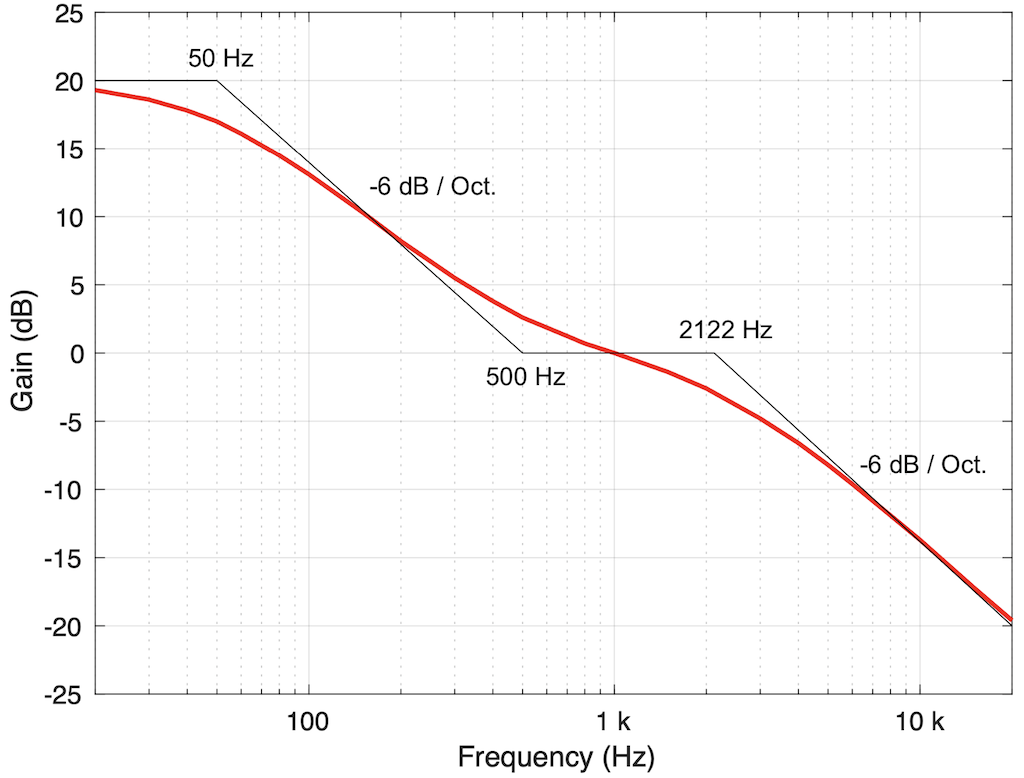
RIAA

• A pre-emphasis / de-emphasis filter designed to fill two functions.
  • The first is a high-frequency attenuation de-emphasis that reduces the playback system’s sensitivity to surface noise. This requires a reciprocal high-frequency pre-emphasis boost.
  • The second is a low-frequency attenuation pre-emphasis that maintains a constant modulation amplitude at lower frequencies to avoid over-excursion of the playback stylus. This requires a reciprocal low-frequency de-emphasis boost.
• The first of the two plots below, show the theoretical (black lines) and typical (red) response of the pre-emphasis filter. The second of the two plots shows the de-emphasis filter response.

Side Thrust

• definition to come

Skating Force

• definition to come

Spindle

• The centre of the platter around which the record rotates

Stylus

• Also known as the needle. The point that is placed in the groove of the vinyl record.
  Some persons distinguish between the “stylus” (to indicate the chisel on the mastering lathe that creates the groove in the master record), and the “needle” (to indicate the portion of the pickup on a turntable that plays the signal).

Stylus, Bonded vs. Nude

• Although the tip of the stylus is typically made of diamond today, in lower-cost units, that diamond tip is mounted or bonded to a metal pin (typically steel, aluminium, or titanium) which is, in turn, connected to the cantilever (the long “arm” that connects back to the cartridge housing). This bonded design is cheaper to manufacture, but it results in a high mass at the stylus tip, which means that it will not move easily at high frequencies.
• In order to reduce mass, the metal pin is eliminated, and the entire stylus is made of diamond instead. This makes things more costly, but reduces the mass dramatically, so it is preferred if the goal is higher sound performance. This design is known as a nude stylus.

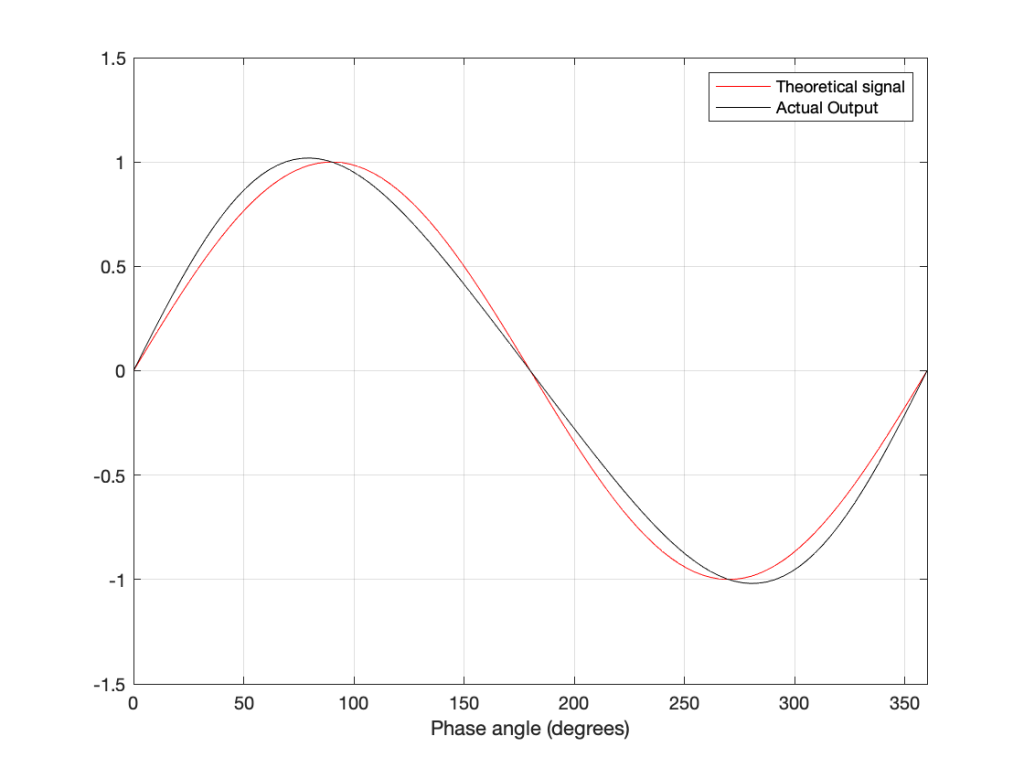
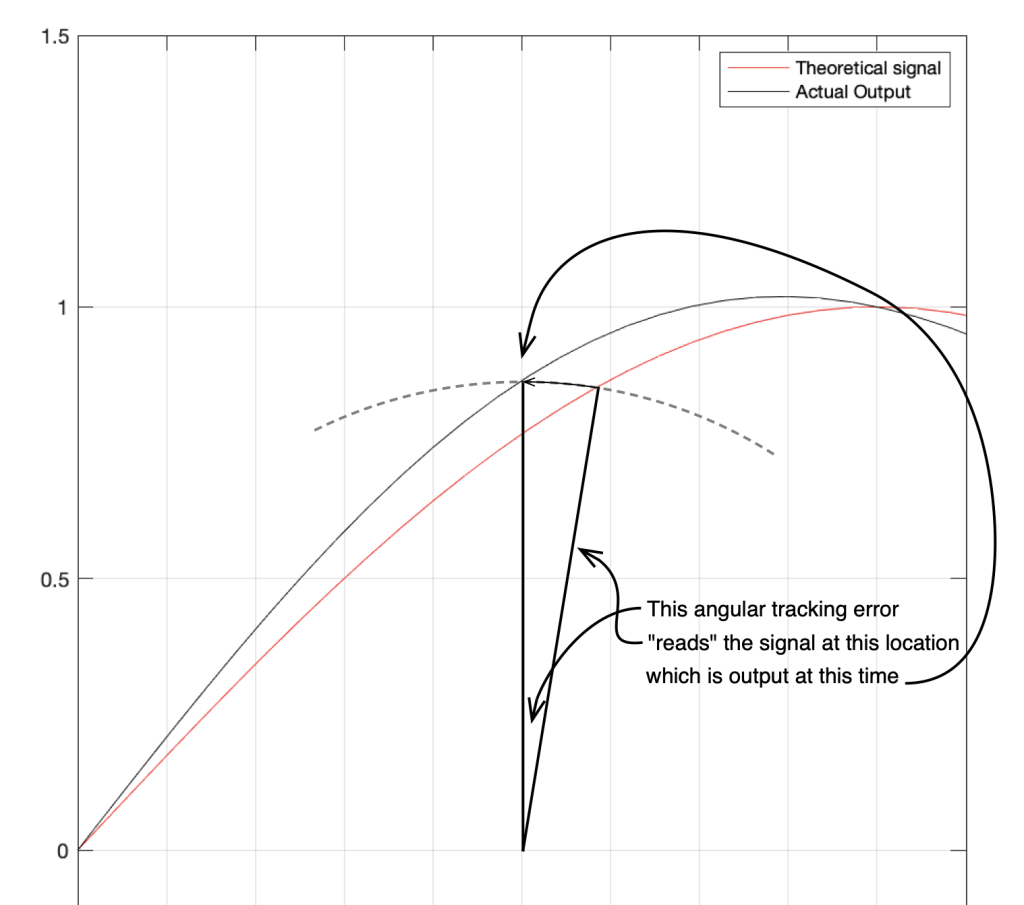
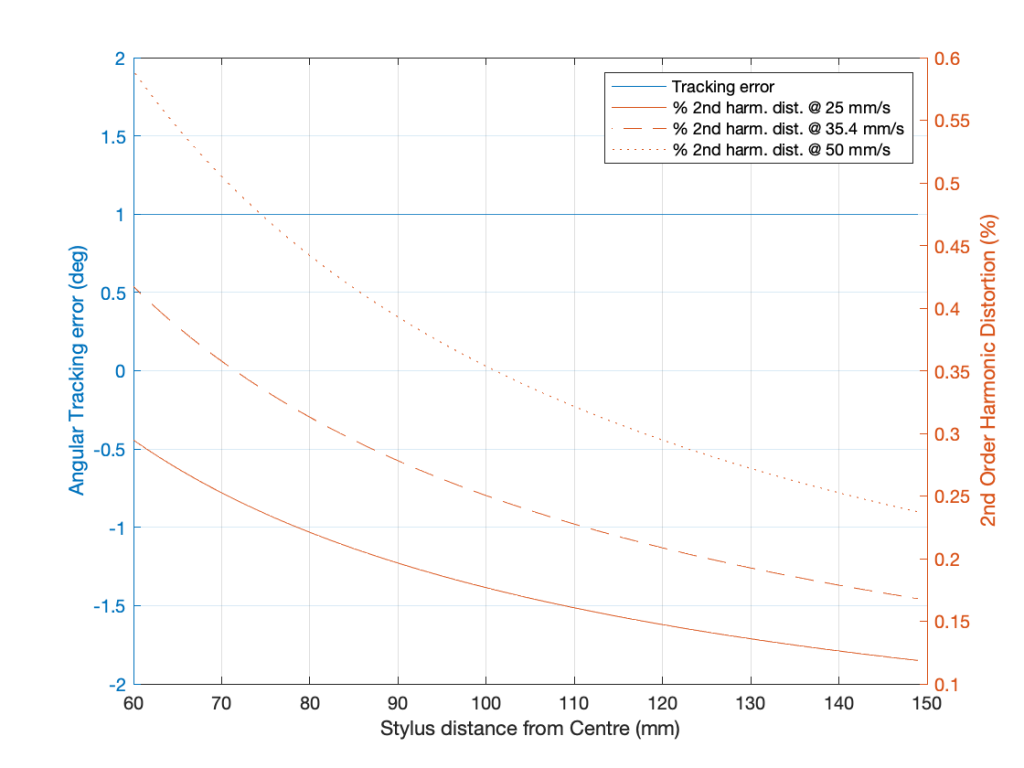
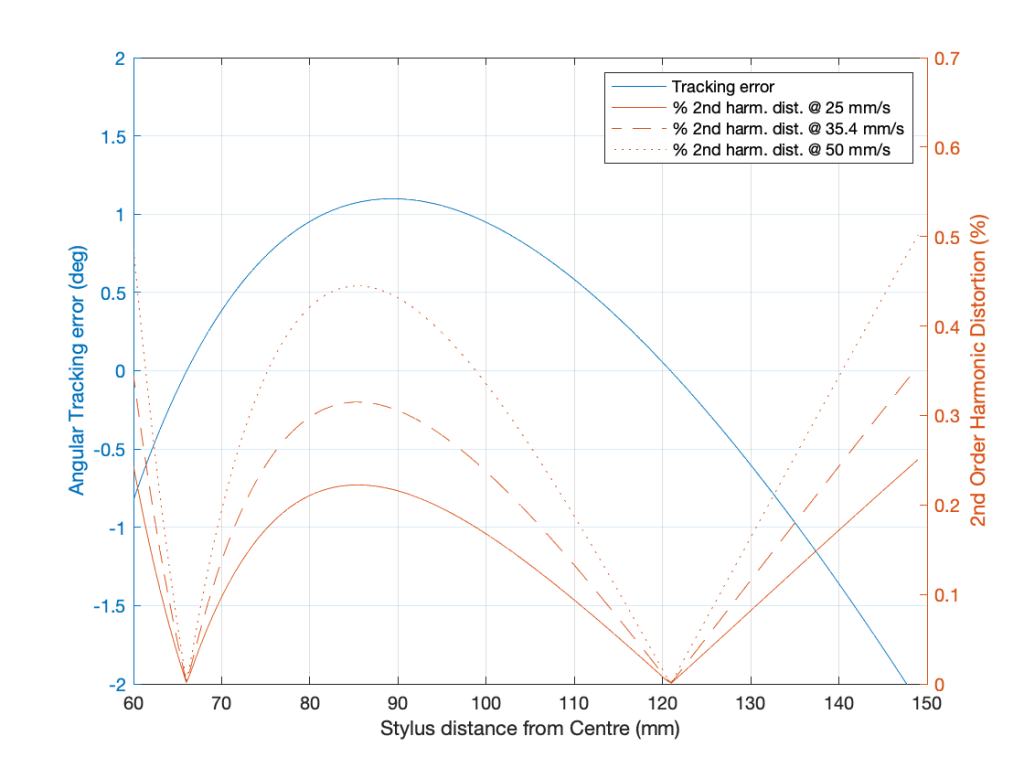
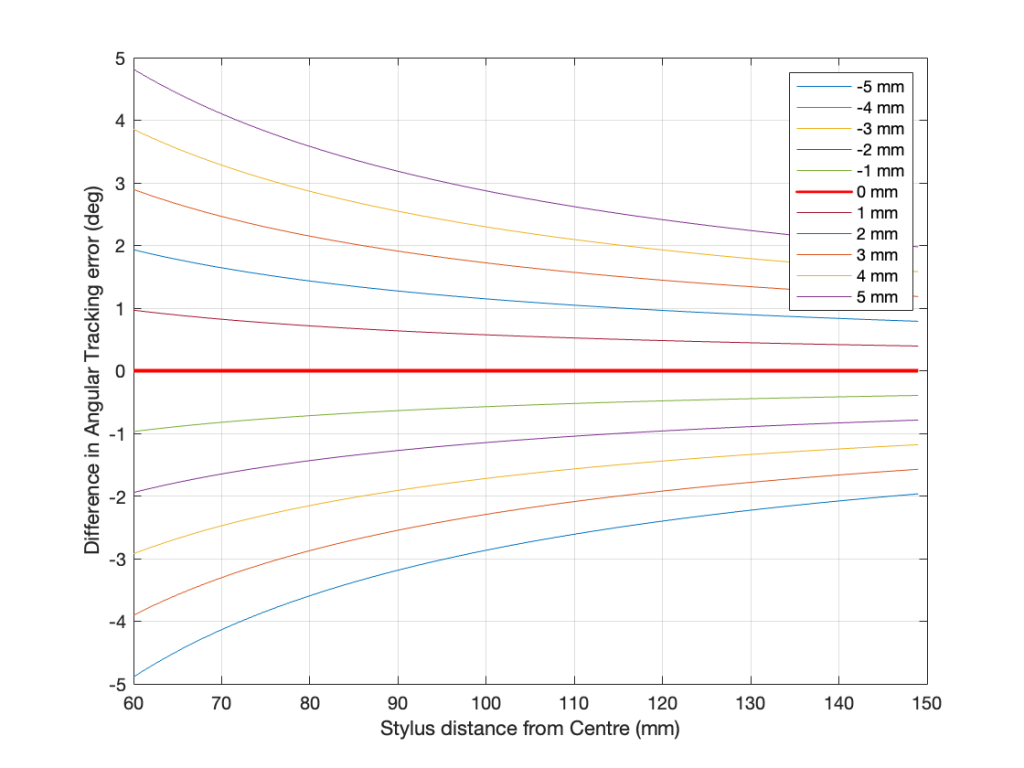
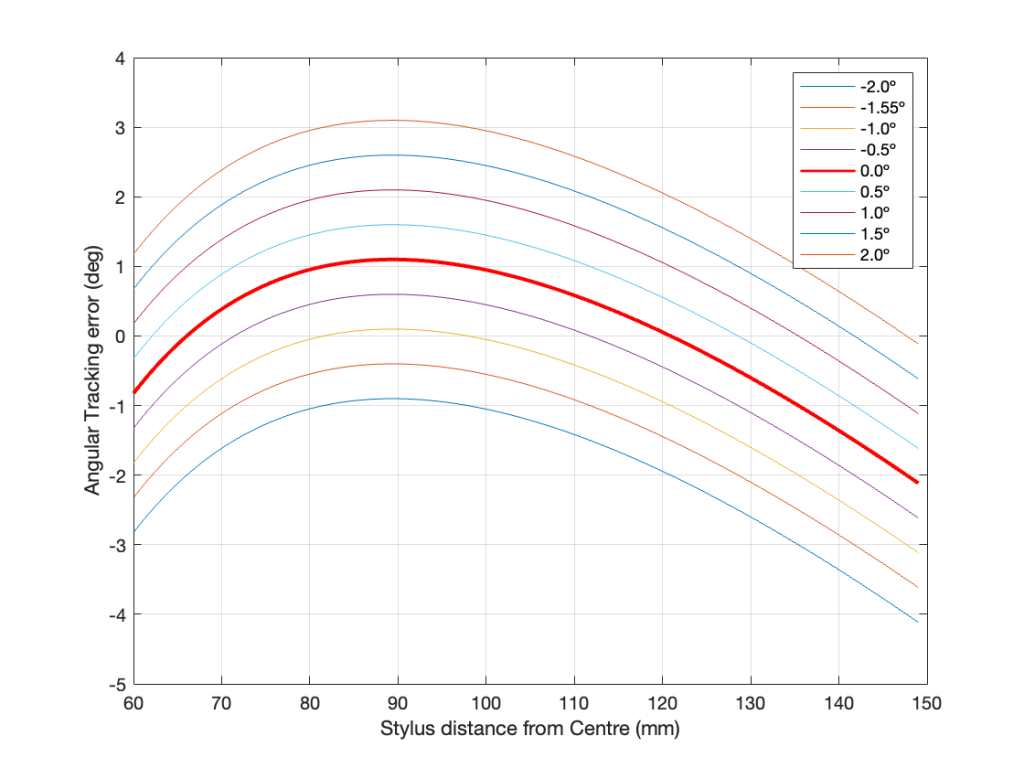
Tracking Error

• The angle between the tangent to the groove and the alignment of the stylus. In a perfect system, the stylus would align with the tangent to the groove at all radii (distances from the spindle), since this matches the angular rotation of the cutting head when the master was made on a lathe. A linear tracking arm minimises this error. A radial tracking arm can be designed to have two radii with no tracking error (each called a “Null Radius”) but will have some measurable tracking error at all other locations on the disk.
• One side-effect of tracking error is distortion of the audio signal, typically calculated and expressed as a 2nd-harmonic distortion on a sinusoidal audio signal. However, higher order distortion and intermodulation artefacts also exist.

Warp Wow

• A modulation of the frequency of the audio signal caused by vertical changes in the vinyl surface (a warped record). This typically happens at a lower frequency, which is why it is “warp wow” and not “warp flutter”.

Wow

• Low-frequency modulation of the audio frequency caused by changes in the groove speed. These may be the result of changes in problems such as rotation speed of the platter, discs with an incorrectly-placed centre hole, or vertical changes in the surface of the vinyl, and other issues.
• Wow is a modulation in the groove speed ranging from once every 2 seconds to 6 times a second (0.5 Hz to 6 Hz). Note that, for a turntable, the rotational speed of the disc is within this range. (At 33 1/3 RPM: 1 revolution every 1.8 seconds is equal to approximately 0.556 Hz.)

Disk size limits

Outside starting diameter

• 7″ discs
  • 6.78″, +0.06″, -0.00″
  • 172.2 mm, +1.524 mm, – 0.0 mm
• 10″ discs
  • 9.72″, +0.06″, -0.00″
  • 246.9 mm, +1.524 mm, – 0.0 mm
• 12″ discs
  • 11.72″, +0.06″, -0.00″
  • 297.7 mm, +1.524 mm, – 0.0 mm

Start of modulated pitch diameter

• 7″ discs
  • 6.63″, +0.00″, -0.03″
  • 168.4 mm, +0.0 mm, – 0.762 mm
• 10″ discs
  • 9.50″, +0.00″, -0.03″
  • 241.3 mm, +0.0 mm, – 0.762 mm
• 12″ discs
  • 11.50″, +0.00″, -0.03″
  • 292.1 mm, +0.0 mm, – 0.762 mm

Minimum inside diameter

• 7″ discs
  • 4.25″
  • 107.95 mm
• 10″ discs
  • 4.75″
  • 120.65 mm
• 12″ discs
  • 4.75″
  • 120.65 mm

Lockout Groove diameter

• 7″ discs
  • 3.88″, +0.00, -0.08
  • 98.552 mm, +0.0 mm, -2.032 mm
• 10″ discs
  • 4.19″, +0.00, -0.08
  • 106.426 mm, +0.0 mm, -0.762 mm
• 12″ discs
  • 4.19″, +0.00, -0.08
  • 106.426 mm, +0.0 mm, -0.762 mm

Unmodulated (silent) groove width

• 2 mil minimum, 4 mil maximum
• 0.0508 mm minimum, 0.1016 mm maximum

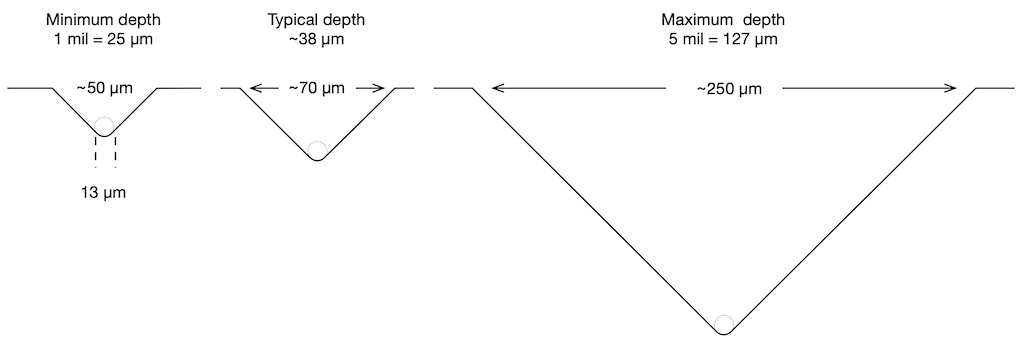
Modulated groove depth

• 1 mil minimum, 5 mil maximum
• 0.0254 mm minimum, 0.127 mm maximum
• The figure below shows the typical, minimum, and maximum groove depths, drawn to scale (with a 13 µm spherical stylus)

Signal levels

• A typical standard reference level is a velocity of 35.4 mm/sec on one channel.
• This means that a monophonic signal (identical signal in both channels) with that modulation will have a lateral (side-to-side) velocity of 50 mm/sec.

Calculators and Measurements

Conversion

• 1 mil = 1 “thou” = 1/1000 inch
• Length_mm = Length_mil * 127/5000

Revolutions per Second

• RevolutionsPerSecond = RevolutionsPerMinute / 60
• e.g.
  • 0.556 Rev/Sec @ 33 1/3 RPM
  • 0.75 Rev/Sec @ 45 RPM
  • 1.3 Rev/Sec @ 78 RPM

Seconds per revolution

• SecondsPerRevolution = 60 / RevolutionsPerMinute
• e.g.
  • 1.8 Sec/Rev @ 33 1/3 RPM
  • 1.333 Sec/Rev @ 45 RPM
  • 0.769 Sec/Rev @ 78 RPM

Modulation Width

• MaximumModulationWidth = (StartOfModulatedPitch – MinimumInsideDiameter) / 2
• e.g. for a 12″ disc
  • (292.1 mm – 120.65 mm) / 2 = 85.725 mm
  • Typically approximately 3″ = 76 mm

Pitch (assuming constant pitch)

• (RunningTime * RPM) / ModulationWidth
• e.g.
  • (20 minutes * 33.333 RPM) / 76 mm = 8.77 lines per mm
  • (20 minutes * 33.333 RPM) / 3″ = 222.22 lines per inch

Groove Width

• GrooveWidthInMil = (1000 / PitchInLinesPerInch + 1) / 2
• e.g.
  • (1000 / 222 LPI + 1) / 2 = 2.75 mil = 2.75 x 10^-3 inches = 0.07 mm

Angular Frequency (of the audio)

• abbreviated ω (unit: radians per second)
• ω = 2 * π * Frequency_Hz

Angular Speed of Rotation (of of the disk)

• commonly abbreviated ω_r (unit: radians per second)
• ω_r = 2 * π * RevolutionsPerSecond

Displacement Amplitude

• DisplacementAmplitude_Peak = Velocity_peak / ω
• e.g.
  • 50 mm/sec / (2 * pi * 1000 Hz) = 0.008 mm (peak)

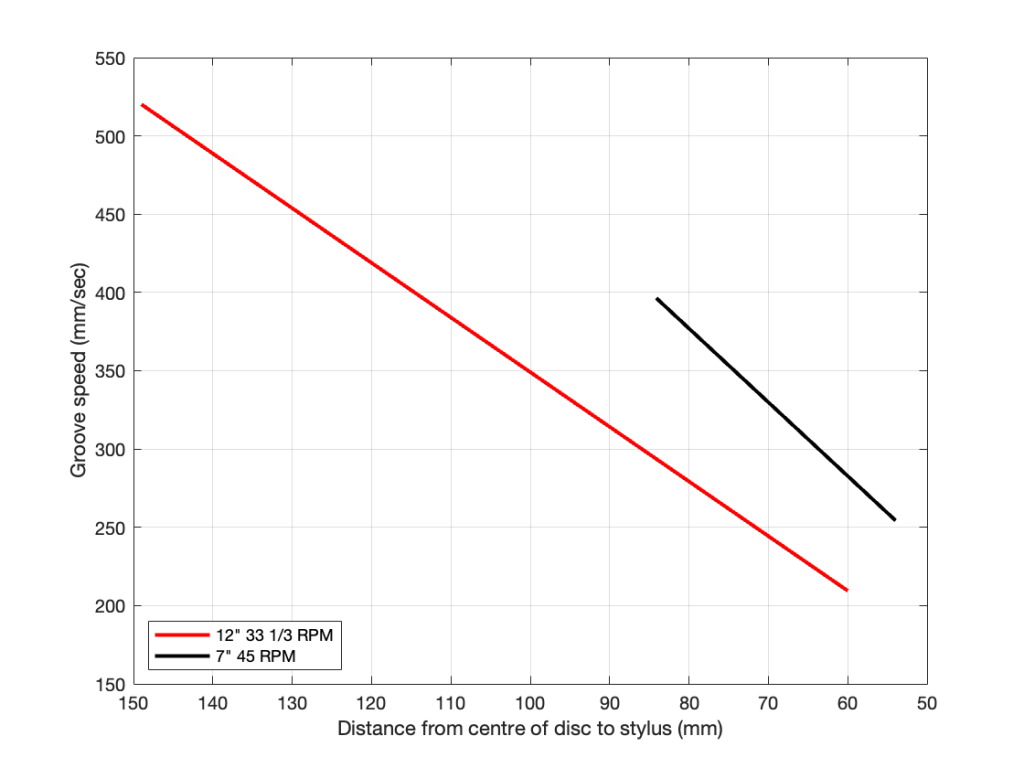
Groove Speed

• 2 * π * Radius * RevolutionsPerSecond
• e.g.
  • at the Start of modulated pitch on a 12″ disk turning at 33 1/3 RPM
    • 2 * π * (292.1 mm / 2) * (33.333 / 60) = 509.8 mm/sec
  • at the Minimum inside diameter on a 12″ disk turning at 33 1/3 RPM
    • 2 * π * (120.65 mm / 2) * (33.333 / 60) = 210.6 mm/sec
• The plot below shows the groove speeds of 12″ 33 1/3 RPM and 7″ 45 RPM for all possible radii.

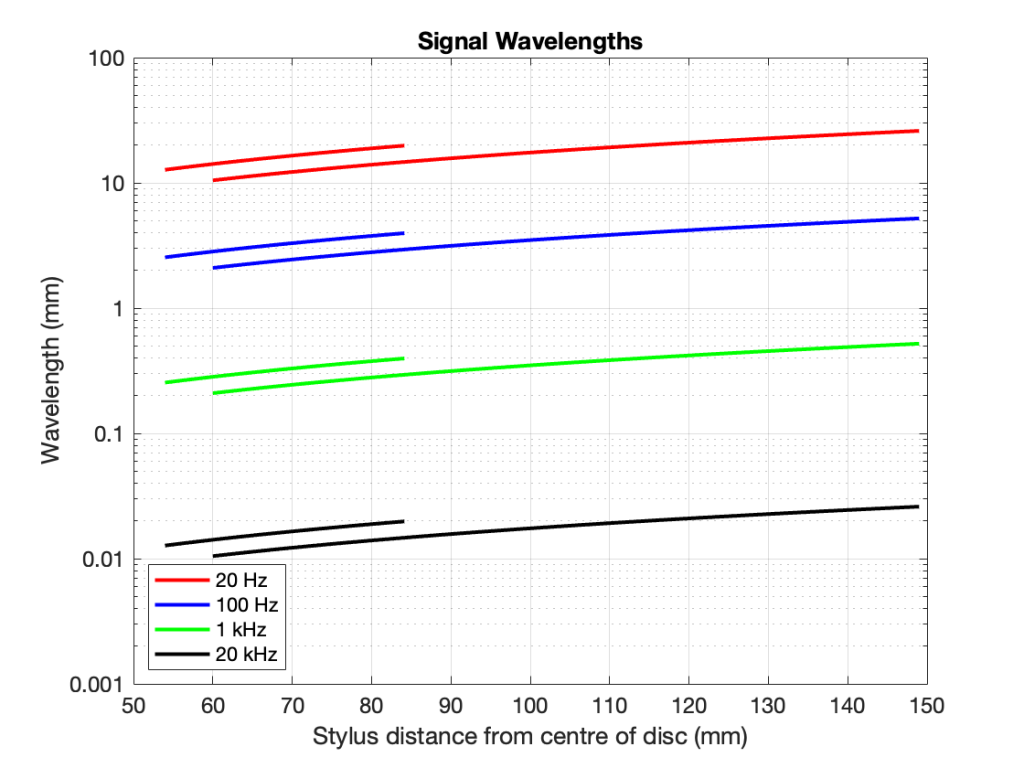
Wavelength

• GrooveSpeed / Frequency
• e.g.
  • 20 Hz at the Start of modulated pitch on a 12″ disk turning at 33 1/3 RPM
    • 509.8 / 20 = 25.5 mm
  • 20 kHz at the Start of modulated pitch on a 12″ disk turning at 33 1/3 RPM
    • 509.8 / 20000 = 0.0255 mm
  • The plot below shows wavelengths of 4 different frequencies for 12″ 33 1/3 RPM records (the longer curves) and 7″ 45 RPM records (the shorter curves)

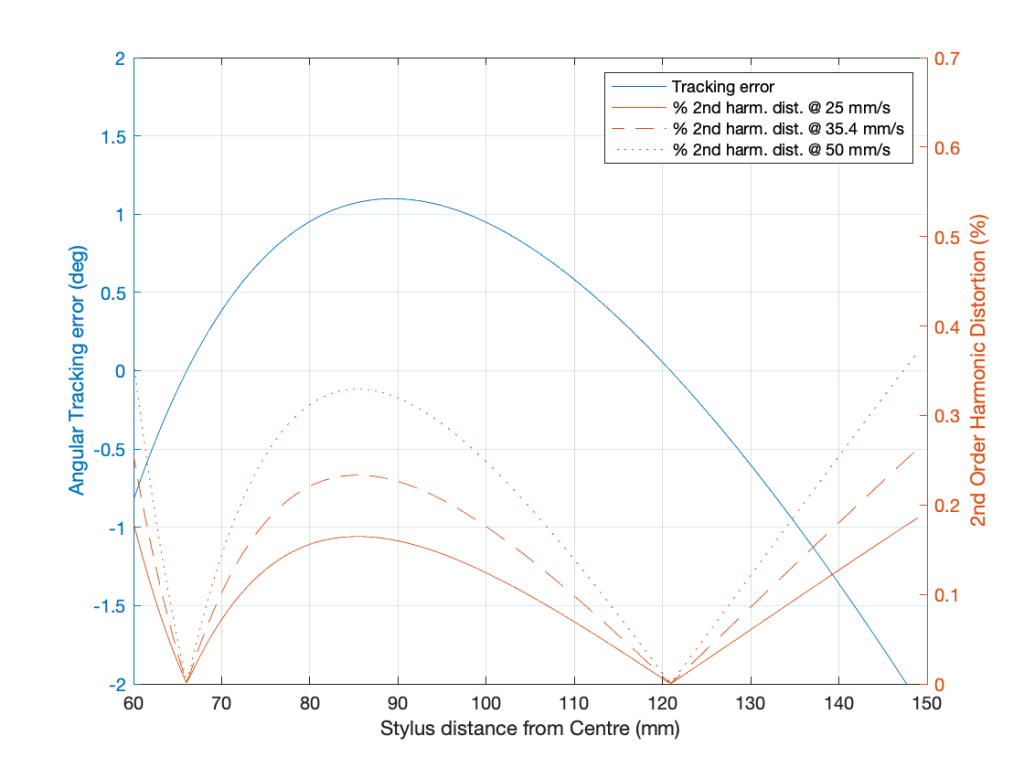
Tracking Error

• Tracking Error =
  OffsetAngle – asin ((EffectiveLength² + Radius² – MountingDistance²) / (2 * EffectiveLength * Radius))
• see this posting for an explanation and example

Distortion caused by tracking error

• Equation is for calculating percentage of second-harmonic distortion of a laterally-modulated monophonic sinusoidal audio signal
• Distortion_Percent = 100 * (PeakVelocity * tan(TrackingError)) / (GrooveSpeed)
• see this posting for an explanation and examples

Wow and Flutter

• Typically measured with a 3150 Hz sinusoidal tone, played from the vinyl surface
• This signal is then de-modulated to determine its change over time. That modulation is then filtered through the response shown below which approximates human sensitivity to frequency modulation of an audio signal. More detailed information is given below

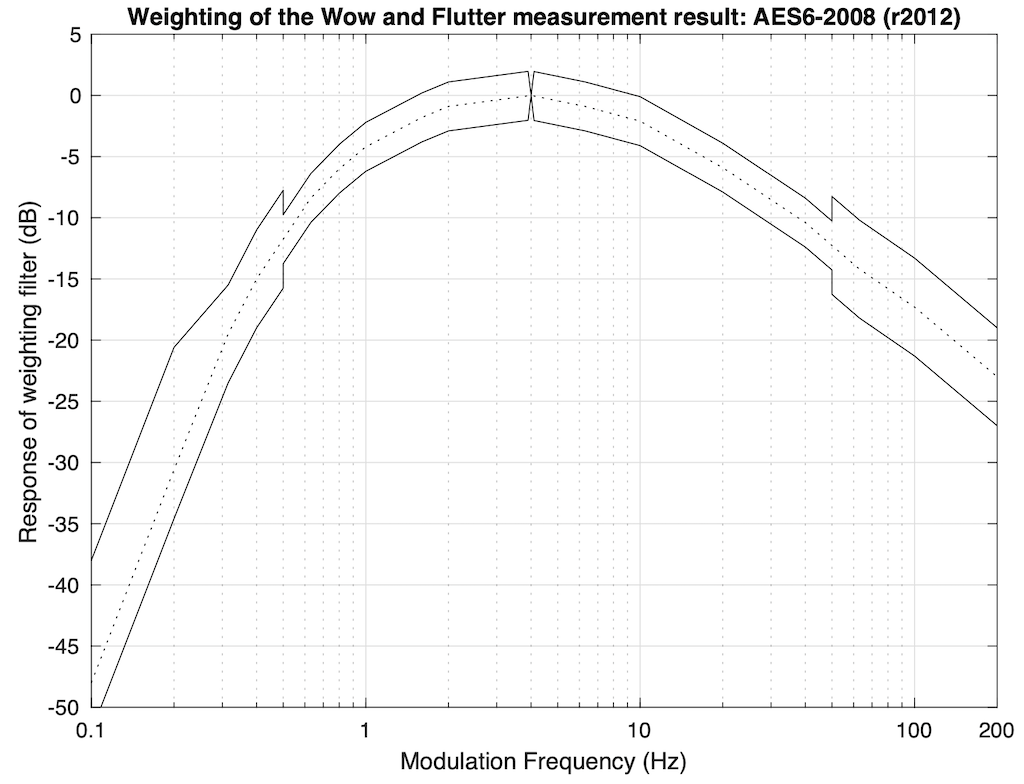
• The AES6-2008 standard, which is the currently accepted method of measuring and expressing the wow and flutter specification, uses a “2σ” or “2-Sigma” method, which is a way of looking at the peak deviation to give a kind of “worst-case” scenario. In this method, the tone is played from a disc and captured for as long a time as is possible (or feasible). Firstly, the average value of the actual frequency of the output is found (in theory, it’s fixed at 3,150 Hz, but this is never true). Next, the short-term variation of the actual frequency over time is compared to the average, and weighted using the filter shown above. The result shows the instantaneous frequency variations over the length of the captured signal, relative to the average frequency (however, the effect of very slow and very fast changes have been reduced by the filter). Finally, the standard deviation of the variation from the average is calculated, and multiplied by 2 (hence “2-Sigma”, or “two times the standard deviation”), resulting in the value that is shown as the specification. The reason two standard deviations is chosen is that (in the typical case where the deviation has a Gaussian distribution) the actual Wow & Flutter value should exceed this value no more than 5% of the time.

References

All of these are available online. Some of them require you to purchase them (or be a member of an organisation).

• “Tracking Angle in Phonograph Pickups”
  B. B. Bauer. Electronics magazine, March 1945
• “Minimising Pickup Tracking Error”
  Dr. John D. Seagrave, Audiocraft Magazine, December 1956, January 1957, and August 1957
• “Understanding Phono Cartridges”
  S.K. Pramanik, Audio magazine, March 1979
• “Tonearm Geometry and Setup Demystified”
  Martin D. Kessler and B.V.Pisha, Audio magazine, January 1980
• “Understanding Tonearms”
  S.K. Pramanik, Audio magazine, June 1980
• “Analytic Treatment of Tracking Error and Notes on Optimal Pick-up Design”
  H.G.Baerwald, Journal of the Society of Motion Picture Engineers, December 1941
• “Pickup Arm Design”
  J.K. Stevenson, Wireless World magazine, May 1966, and June 1966
• “The Optimum Pivot Position on Tonearm”
  S. Takahashi et. al., Audio Engineering Society Preprint no. 1390 (61st Convention, November 1978)
• “Audible Effects of Mechanical Resonances in Turntables”
  Brüel and Kjær Application Note (1977)
• “Basic Disc Mastering”; “
  Larry Boden (1981)
• “Cartridge / Arm / Turntable Followup: Loose Ends and New Developments”
  The Audio Critic, 1:43 (Spring/Fall, 1978)
• “Have Tone Arm Designers Forgotten Their High-School Geometry?”
  The Audio Critic, 1:31 (Jan./Feb. 1977).
• “How the Stereo Disc Works”
  Radio-Electronics, (July 1958)
• “Manual of Analogue Sound Restoration Techniques”
  Peter Copeland (2008)
• “On the Mechanics of Tonearms”
  Dick Pierce (2005)
• “Reproduction of Sound in High-Fidelity and Stereo Phonographs”
  Edgar Villchur (1966)
• Journal of the Audio Engineering Society (www.aes.org)
  • “Centennial Issue: The Phonograph and Sound Recording After One-Hundred Years”
    Vol. 25, No. 10/11 (Oct./Nov. 1977)
  • “Factors Affecting the Stylus / Groove Relationship in Phonograph Playback Systems”
    C.R. Bastiaans; Vol. 15 Issue 4 (Oct. 1967)
  • “Further Thoughts on Geometric Conditions in the Cutting and Playing of Stereo Disk”
    C.R. Bastiaans; Vol. 11 Issue 1 (Jan. 1963)
  • “Record Changers, Turntables, and Tone Arms-A Brief Technical History”
    James H. Kogen; Vol. 25 (Oct./Nov. 1977)
  • “Some Thoughts on Geometric Conditions in the Cutting and Playing of Stereodiscs and Their Influence on the Final Sound Picture”
    Ooms, Johan L., Bastiaans, C. R.; Vol. 7 Issue 3 (Jul. 1959)
  • “The High-Fidelity Phonograph Transducer”
    B.B. Bauer; Vol. 25 Issue 10/11 (Nov. 1977)
• DIN Standards
  • 45 500: Hi-Fi Technics: Requirements for Disk Recording Reproducing Equipment
  • 45 507: Measuring Apparatus for Frequency Variations in Sound Recording Equipment
  • 45 538: Definitions for Disk Record Reproducing Equipment
  • 45 539: Disk Record Reproducing Equipment: Directives for Measurements, Markings, and Audio Frequency, Connections, Dimensions of Interchangeable Pickups, Requirements of Playback Amplifiers
  • 45 541: Frequency Test Record St 33 and M 33 (33 1/3 rev/min; Stereo and Mono)
  • 45 542: Distortion Test Record St 33 and St 45 (33 1/3 or 45 rev/min; Stereo)
  • 45 543: Frequency Response and Crosstalk Test Record
  • 45 544: Rumble Measurement Test Record St 33 and M 33 (33 1/3 rev/min; Stereo and Mono)
  • 45 545: Wow and Flutter Test Records, 33 1/3 and 45 rev/min
  • 45 546: Stereophonic Disk Record St 45 (45 rpm)
  • 45 547: Stereophonic Disk Record St 33 (33 1/3 rpm)
  • 45 548 Aptitude for Performance of Disk Record Reproducing Equipment
  • 45 549: Tracking Ability Test Record
• IEC Publications
  • 98: Recommendations for Lateral-Cut Commercial and Transcription Disk Recordings
  • 98: Processed Disk Records and Reproducing Equipment
  • 386: Method of Measurement of Speed Fluctuations in Sound Recording and Reproducing Equipment

In the last posting, I reviewed the math for calculating the tracking error for a radial tonearm. The question associated with this is “who cares?”

In the March, 1945 issue of Electronics Magazine, Benjamin Bauer supplied the answer. An error in the tracking angle results in a distortion of the audio signal. (This was also discussed in a 3-part article by Dr. John D. Seagrave in Audiocraft Magazine in December 1956, January 1957, and August 1957)

If the signal is a sine wave, then the distortion is almost entirely 2nd-order (meaning that you get the sine wave fundamental, plus one octave above it). If the signal is not a sine wave, then things are more complicated, so I will not discuss this.

Let’s take a quick look at how the signal is distorted. An example of this is shown below.

In that plot, you can see that the actual output from the stylus with a tracking error (the black curve) precedes the theoretical output that’s actually on the vinyl surface (the red curve) when the signal is positive, and lags when it’s negative. An intuitive way of thinking of this to consider the tracking error as an angular rotation, so the stylus “reads” the signal in the groove at the wrong place. This is shown below, which is merely zooming in on the figure above.

Here, you can see that the rotation (tracking error) of the stylus is getting its output from the wrong place in the groove and therefore has the wrong output at any given moment. However, the amount by which it’s wrong is dependent not only on the tracking error but the amplitude of the signal. When the signal is at 0, then the error is also 0. This is not only the reason why the distortion creates a harmonic of the sine wave, but it also explains why (as we’ll see below) the level of distortion is dependent on the level of the signal.

This intuitive explanation is helpful, but life is unfortunately, more complicated. This is because (as we saw in the previous posting), the tracking error is not constant; it changes according to where the stylus is on the surface of the vinyl.

If you dig into Bauer’s article, you’ll find a bunch of equations to help you calculate how bad things get. There are some minor hurdles to overcome, however. Since he was writing in the USA in 1945, his reference was 78 RPM records and his examples are all in inches. However, if you spend some time, you can convert this to something more useful. Or, you could just trust me and use the information below.

In the case of a sinusoidal signal the level of the 2nd harmonic distortion (in percent) can be calculated with the following equation:

PercentDistortion = 100 * (ω Α_peak α) / (ω_r r)

where

• ω is 2 * pi * the audio frequency in Hz
• A_peak is the peak amplitude of the modulation (the “height” of the groove) in mm
• α is the tracking error in radians
• ω_r is the rotational speed of the record in radians per second, calculated using 2 * pi * (RPM / 60)
• r is the radius of the groove; the distance from the centre spindle to the stylus in mm

Let’s invent a case where you have a constant tracking error of 1º, with a rotational speed of 33 1/3 RPM, and a frequency of 1 kHz. Even though the tracking error remains constant, the signal’s distortion will change as the needle moves across the surface of the record because the wavelength of the signal on the vinyl surface changes (the rotational speed is the same, but the circumference is bigger at the outside edge of the record than the inside edge). The amount of error increases as the wavelength gets smaller, so the distortion is worse as you get closer to the centre of the record. This can be see in the shapes of the curves in the plot below. (Remember that, as you play the record, the needle is moving from right to left in those plots.)

You can also see in those plots that the percentage of distortion changes significantly with the amplitude of the signal. In this case, I’ve calculated using three different modulation velocities. The middle plot is 35.4 mm / sec, which is a typical accepted standard reference level, which we’ll call 0 dB. The other two plots have modulation velocities of -3 dB (25 mm / sec) and + 3 dB (50 mm / sec).

Sidebar: If you want to calculate the Amplitude of the modulation

A_peak = (ModulationVelocity * sqrt(2)) / (2 * pi * FrequencyInHz)

Note that this simplifies the equation for calculating the distortion somewhat.

Also, if you need to convert radians to degrees, then you can multiply by 180/pi. (about 57.3)

Of course, unless you have a very badly-constructed linear tracking turntable, you will never have a constant tracking error. The tracking error of a radial tonearm is a little more complicated. Using the recommended values for the “well known tonearm” that I used in the last posting:

• Effective Length (l) : 233.20 mm
• Mounting Distance (d) : 215.50 mm
• Offset angle (y) : 23.63º

and assuming that this was done perfectly, we get the following result for a 33 1/3 RPM album.

You can see here that the distortion drops to 0% when the tracking error is 0º, which (in this case) happens at two radii (distances between the centre spindle and the stylus).

If we do exactly the same calculation at 45 RPM, you’ll see that the distortion level drops (because the value of ω_r increases), as shown below. (But good luck finding a 12″ 45 RPM record… I only have two in my collection, and one of those is a test record.)

Important notes:

Everything I’ve shown above is not to be used as proof of anything. It’s merely to provide some intuitive understanding of the relationship between radial tracking tonearms, tracking error, and the resulting distortion. There is one additional important reason why all this should be taken with a grain of salt. Remember that the math that I’ve given above is for 78 RPM records in 1945. This means that they were for laterally-modulated monophonic grooves; not modern two-channel stereophonic grooves. This means that the math above isn’t accurate for a modern turntable, since the tracking error will be 45º off-axis to the axis of modulation of the groove wall. This rotation can be built into the math as a modification applied to the variable α, however, I’m not going to complicate things further today…

In addition, the RIAA equalisation curve didn’t get standardised until 1954 (although other pre-emphasis curves were being used in the 1940s). Strictly speaking, the inclusion of a pre-emphasis curve doesn’t really affect the math above, however, in real life, this equalisation makes it a little more complicated to find out what the modulation velocity (and therefore the amplitude) of the signal is, since it adds a frequency-dependent scaling factor on things. On the down-side, RIAA pre-emphasis will increase the modulation velocity of the signal on the vinyl, resulting in an increase in the distortion effects caused by tracking error. On the up-side, the RIAA de-emphasis filtering is applied not only to the fundamentals, but the distortion components as well, so the higher the order of the unwanted harmonics, the more they’ll be attenuated by the RIAA filtering. How much these two effects negate each other could be the subject of a future posting; if I can wrap my own head around the problem…

One extra comment for the truly geeky:

You may be looking at the last two plots above and being confused in the same way that I was when I made them the first time. If you look at the equation, you can see that the PercentDistortion is related to α: the tracking error. However, if you look at the plots, you’ll see that I’ve shown it as being related to | α |: the absolute value of the tracking error instead. This took me a while to deal with, since my first versions of the plots were showing a negative value for the distortion. “How can a negative tracking result in distortion being removed?” I asked myself. The answer is that it doesn’t. When the tracking error is negative, then the angle shown in the second figure above rotates counter-clockwise to the left of the vertical line. In this case, then the output of the stylus lags for positive values and precedes for negative values (opposite to the example I gave above), meaning that the 2nd-order harmonic flips in polarity. SINCE you cannot compare the phase of two sine tones that do not have the same frequency, and SINCE (for these small levels of distortion) it’ll sound the same regardless of the polarity of the 2nd-order harmonic, and SINCE (in real-life) we don’t listen to sine tones so we get higher-order THN and IMD artefacts, not just a frequency doubling, THEN I chose to simplify things and use the absolute value.
Post Script to the comment for geeks: This conclusion was confirmed by J.K. Stevenson’s article called “Pickup Arm Design” in the May, 1966 edition of Wireless World where he states “The sign of φ (positive or negative) is ignored as it has no effect on the distortion.” (He uses φ to denote the tracking error angle.)

Penultimate Post Script:

J.K. Stevenson’s article gives an alternative way of calculating the 2nd order harmonic distortion that gives the same results. However, if you are like me, then you think in modulation velocity instead of amplitude, so it’s easier to not convert on the way through. This version of the equation is

PercentDistortion = 100 * (V_peak tan(α)) / (μ)

where

• V_peak is the peak modulation velocity in mm/sec
• α is the tracking error in radians
• μ is the groove speed of the record in mm/sec calculated using 2*pi*(rpm/60)*r
• r is the radius of the groove; the distance from the centre spindle to the stylus in mm

Final Post-Script:

I’ve given this a lot of thought over the past couple of days and I’m pretty convinced that, since the tracking error is a rotation angle on an axis that is 45º away from the axis of modulation of the stylus (unlike the assumption that we’re dealing with a monophonic laterally-modulated groove in all of the above math), then, to find the distortion for a single channel of a stereophonic groove, you should multiply the results above by cos(45º) or 1/sqrt(2) or 0.707 – whichever you prefer. If you are convinced that this was the wrong thing to do, and you can convince me that you’re right, I’ll be happy to change it to something else.