B&O Tech: BeoLab loudspeakers and Third-party systems

#77 in a series of articles about the technology behind Bang & Olufsen loudspeakers

I’m occasionally asked about the technical details of connecting Bang & Olufsen loudspeakers to third-party (non-B&O) sources. In the “old days”, this was slightly difficult due to connectors, adapters, and outputs. However, that was a long time ago – although beliefs often persist longer than facts…

All Bang & Olufsen “BeoLab” loudspeakers are “active”. At the simplest level, this means that the amplifiers are built-in. In addition, almost all of the BeoLab loudspeakers in the current portfolio use digital signal processing. This means that the filtering and crossovers are implemented using a built-in computer instead of using resistors, capacitors, and inductors. This will be a little important later in this posting.

In order to talk about the compatibility issues surrounding the loudspeakers in the BeoLab portfolio – both with themselves and with other loudspeakers, we really need to break the discussion into two areas. The first is that of connectors and signals. The second, more problematic issue is that of “latency” (which is explained below…)

Connectors and signals

Since BeoLab loudspeakers have the amplifiers built-in, you need to connect them to an analogue “line level” signal instead of the output of an amplifier.

This means that, if you have a stereo preamplifier, then you just connect the “volume-regulated” Line Output of the preamp to the RCA line inputs of the BeoLab loudspeakers. (Note that the BeoLab 3 does not have a built-in RCA connector, so you need an adapter for this). Since the BeoLab loudspeakers (except for BeoLab 5, 50, and 90) are fixed at “full volume”, then you need to ensure that your Line Output of the source is, indeed, volume-regulated. If not, things will be surprisingly loud…

In addition to the RCA Line inputs, most BeoLab loudspeakers also have at least one digital audio input. The BeoLab 5 has an S/P-DIF “coaxial” input. The BeoLab 17, 18, and 20 have optical digital inputs. The BeoLab 50 and 90 have many options to choose from. Again, apart from the BeoLab 5, 50, and 90, the loudspeakers are fixed at “full volume”, so if you are going to use the digital input for the BeoLab 17, 18, or 20, you will need to enable the volume regulation of the digital output of your source, if that’s possible.

Latency

Any audio device has some inherent “latency” or “delay from the time the signal comes in until it goes out”. For some devices, this latency can be so low that we can think of it as being 0 seconds. In other words, for some devices (say, a wire, for example) the signal comes out at the same time as it comes in (as far as we’re concerned… I’m not going to get into an argument about the speed of electricity or light, since these go very fast…)

Any audio device that uses digital signal processing has some measurable (and possibly audible) latency. This is primarily due to 5 things, seen in the flowchart below.

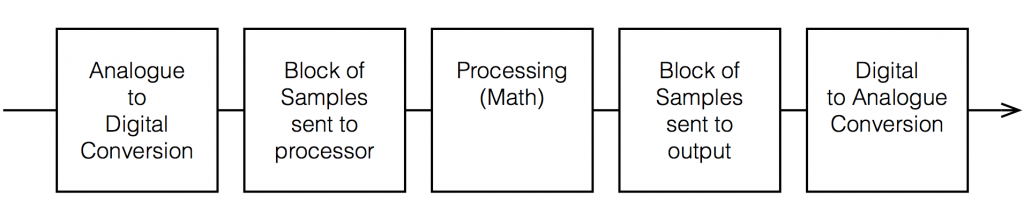
Fig 1. The basic steps that cause latency in a digital audio system that has an analogue input and output.

Each of these 5 steps each have different amounts of latency – some of them very, very small. Some are bigger. One thing to know about digital signal processing is that, typically, in order to make the math more efficient (and therefore squeeze as much as possible out of the computing power), the samples are processed in “blocks” – not one-by-one. So, the signal comes into the input, it gets converted to individual samples, and those samples are collected into a block of 64 samples (for example) before being sent to the processing.

So, let’s say that you have a sampling rate of 44100 samples per second, and a block size of 64 samples. This then means that you send a block to the processor every 64 * 1/44100 = 1.45 ms. That block gets processed (which takes some time), and then sent as another block of 64 samples to the DAC (digital to analogue converter).

So, ignoring the latency of the conversion from- and to-analogue, in the example above, it will take 1.45 ms to get the signal into the processor, you have a 1.45 time window to do the processing, and it will take another 1.45 ms to get the signal out to the DAC. This is a total of 4.35 ms from the instant a signal gets comes into the analogue input to the moment it comes out the analogue output.

Sidebar: Of course, 4.3 ms is not a long time. If you had a loudspeaker outdoors, then adding 4.35 ms to its latency would be same delay you would incur by moving 1.5 m (or about 4.9 feet) further away. However, in terms of a stereo or multichannel audio system, 4.35 ms is an eternity. For example, if you have a correctly-configured stereo loudspeakers (with each loudspeaker 30º from centre-front, and you’re sitting in the “sweet spot”, if you delay the left loudspeaker by just 0.2 ms, then lead vocals in your pop tunes will move 10º to the right instead of being in the centre. It only takes 1.12 ms of delay in one loudspeaker to move things all the way to the opposite side. In a multichannel loudspeaker configuration (or in headphones), some of the loudspeaker pairs (e.g. Left Surround – Right Surround) result in you being even more sensitive to these so-called “inter-channel delay differences”.

Also, the amount of time required by the processing depends on what kind of processing you’re doing. In the case of BeoLab 50 and 90, for example, we are using FIR filters as part of the directivity (Beam Width and Beam Direction) processing. Since this filtering extends quite low in frequency, the FIR filters are quite long – and therefore they require extra latency. To add a small amount of confusion to this discussion (as we’ll see below) this latency is switchable to be either 25 ms or 100 ms. If you want Beam Width control to extend as low in frequency as possible, you need to use the 100 ms “Long Latency” mode. However, if you need lip-synch with a non-B&O source, you should use the 25 ms “Low Latency” mode (with the consequent loss of directivity control at very low frequencies).

Latency in BeoLab loudspeakers

In order to use BeoLab loudspeakers with a non-B&O source (or an older B&O source) , you may need to know (and compensate for) the latency of the loudspeakers in your system. This is particularly true if you are “mixing and matching” loudspeakers: for example, using different loudspeaker models (or other brands – *gasp*) in a single multichannel configuration.

Model	A / D	Latency (ms)	Equivalent in m	Volume Regulation?
Unknown analogue	A	0	0	No
Beolab 1	A	0	0	No
Beolab 2	A	0	0	No
Beolab 3	A	0	0	No
Beolab 4	A	0	0	No
Beolab 5	D	3.92	1.35	Yes
Beolab 7 series	A	0	0	No
Beolab 9	A	0	0	No
Beolab 12 series	D	4.4	1.51	No
Beolab 17	D	4.4	1.51	No
Beolab 18	D	4.4	1.51	No
Beolab 19	D	4.4	1.51	No
Beolab 20	D	4.4	1.51	No
Beolab 50	D	25 / 100	8.6 / 34.4	Yes
Beolab 90	D	29 / 100	10.0 / 34.4	Yes

Table 1. The latencies and equivalent distances for various BeoLab loudspeakers Notice that the analogue loudspeakers all have a latency of 0 ms.

How to Do It

I’m going to make two assumptions for the rest of this posting:

you have a stereo preamp or a surround processor / AVR that has a “Speaker Distance” or “Speaker Delay” adjustment parameter (measured from the loudspeaker location to the listening position)
it does not have a “loudspeaker latency” adjustment parameter

The simple version (that probably won’t work):

Since the latency of the various loudspeakers can be “translated” into a distance, and since AVR’s typically have a “Speaker Distance” parameter, you simply have to add the equivalent distance of the loudspeaker’s latency to the actual distance to the loudspeaker when you enter it in the menus.

For example, let’s say that you have a 5.0 channel loudspeaker configuration with the following actual speaker distances, measured in the room.

Channel	Model	Distance
Left Front	Beolab 5	3.7
Right Front	Beolab 5	3.9
Centre Front	Beolab 3	3.9
Left Surround	Beolab 17	1.6
Right Surround	Beolab 17	3.2

Table 2. An example of a simple 5.0-channel loudspeaker configuration

You then look up the equivalent distances in the first table and add the appropriate number to each loudspeaker.

Channel	Model	Distance	+	Latency Equivalent	=	Total
Left Front	Beolab 5	3.7	+	1.35	=	5.05
Right Front	Beolab 5	3.9	+	1.35	=	5.25
Centre Front	Beolab 3	3.9	+	0	=	3.9
Left Surround	Beolab 17	1.6	+	1.51	=	3.11
Right Surround	Beolab 17	3.2	+	1.51	=	4.71

Table 3. Calculating the required speaker distances to compensate for the loudspeakers’ latencies using the example in Table 2.

This technique will work fine unless the total distance that you have to enter in the AVR’s menus is greater than its maximum possible value (which is typically 10.0 m on most brands and models that I’ve seen – although there are exceptions).

So, what do you do if your AVR can’t handle a value that’s high enough? Then you need to fiddle with the numbers a bit…

The slightly-more complicated version (which might work most of the time)

When you enter the Speaker Distances in the menus of your AVR, you’re doing two things:

calibrating the delay compensation for the differences in the distances from the listening position to the individual loudspeakers
(maybe) calibrating the system to ensure that the sound arrives at the listening position at the same time as the video is displayed on the screen (therefore sending the sound out early, since it takes longer for the sound to travel to the sofa than it takes the light to get from your screen…)

That second one has a “maybe” in front of it for a couple of reasons:

this is a very small effect, and might have been decided by the manufacturer to be not worth the effort
the manufacturer of an AVR has no way of knowing the latency of the screen to which it’s attached. So, it’s possible that, by outputting the sound earlier (to compensate for the propagation delay of the sound) it’s actually making things worse (because the screen is delayed, but the AVR doesn’t know it…)

So, let’s forget about that lip-synch issue and stick with the “delay compensation for the differences in the distances” issue. Notice that I have now highlighted the word “differences” in italics twice… this is important.

The big reason for entering Speaker Distances is that you want the a sound that comes out of all loudspeakers simultaneously to reach the listening position simultaneously. This means that the closer loudspeakers have to wait for the further loudspeakers (by adding an appropriate delay to their signal path). However, if we ignore the synchronisation to another signal (specifically, the lips on the screen), then we don’t need to know the actual (or “absolute”) distance to the loudspeakers – we only need to know their differences (or “relative distances”). This means that you can consider the closest loudspeaker to have a distance of 0 m from the listening position, and you can subtract that distance from the other distances.

For example, using the table above, we could subtract the distance to the closest loudspeaker (the Left Surround loudspeaker, with a distance of 1.6 m) from all of the loudspeakers in the table, resulting in the table below.

Channel	Model	Distance	–	Closest	=	Result
Left Front	Beolab 5	3.7	–	1.6	=	2.1
Right Front	Beolab 5	3.9	–	1.6	=	2.3
Centre Front	Beolab 3	3.9	–	1.6	=	2.3
Left Surround	Beolab 17	1.6	–	1.6	=	0
Right Surround	Beolab 17	3.2	–	1.6	=	1.6

Table 4. Another version of Table 3, showing how to reduce values to fit the constraints of the AVR if necessary.

Again, you look up the equivalent distances in the first table and add the appropriate number to each loudspeaker.

Channel	Model	Distance	+	Latency equivalent	=	Total
Left Front	Beolab 5	2.1	+	1.35	=	3.45
Right Front	Beolab 5	2.3	+	1.35	=	3.65
Centre Front	Beolab 3	2.3	+	0	=	2.3
Left Surround	Beolab 17	0	+	1.51	=	1.51
Right Surround	Beolab 17	1.6	+	1.51	=	3.11

Table 5. Calculating the required speaker distances to compensate for the loudspeakers’ latencies using the example in Table 4.

As you can see in Table 5, the end results are smaller than those in Table 3 – which will help if your AVR can’t get to a high enough value for the Speaker Distance.

The only-slightly-even-more complicated version (which has a better chance of working most of the time)

Of course, the version I just described above only subtracted the smallest distance from the other distances, however, we could do this slightly differently and subtract the smallest total (actual + equivalent distance) from the totals to “force” one of the values to 0 m. This can be done as follows:

Starting with a copy of Table 3, we get a preliminary Total, and then subtract the smallest of these from all value to get our Final Speaker Distance.

Channel	Model	Distance (m)	+	Latency (m)	=	Total	–	Smallest	=	Final
Lf	BL 5	3.7	+	1.35	=	5.05	–	3.11	=	1.94
Rf	BL 5	3.9	+	1.35	=	5.25	–	3.11	=	2.14
Cf	BL 3	3.9	+	0	=	3.9	–	3.11	=	0.79
Ls	BL17	1.6	+	1.51	=	3.11	–	3.11	=	0
Rs	BL 17	3.2	+	1.51	=	4.71	–	3.11	=	1.6

Table 6. Another version of Table 3, showing how to minimise values to fit the constraints of the AVR if necessary.

Of course, if you do it the first way (as shown in Table 3) and the values are within the limits of your AVR, then you don’t need to get complicated and start subtracting. And, in many cases, if you don’t own BeoLab 50 or 90, and you don’t live in a mansion, then this will probably be okay. However… if you DO own BeoLab 50 or 90, and/or you do live in a mansion, then you should probably get used to subtracting…

Some additional information about BeoLab 50 & 90

As I mentioned above, the BeoLab 50 and BeoLab 90 have two latency options. The “High Latency” option (100 ms) allows us to implement FIR filters that control the directivity (the Beam Width and Beam Directivity) to as low a frequency as possible. However, in this mode, the latency is so high that you will notice that the sound is behind the picture if you have a non-B&O television.* In other words, you will not have “lip-synch”.

For customers with a non-B&O television*, we have included a “Low Latency” option (25 ms) which is within the tolerable limits of lip-synch. In this mode, we are still controlling the directivity of the loudspeaker with an FIR, but it cannot go as low in frequency as the “High Latency” option.

As I mentioned above, a 100 ms latency in a loudspeaker is equivalent to placing it 34.4 m further away (ignoring the obvious implications on the speaker level). If you have a third-part source such as an AVR, it is highly unlikely that you can set a Speaker Distance in the menus to be the actual distance + 34.4 m…

So, in the case of BeoLab 50 or 90, you should manually set the Latency Mode to “Low Latency” (using the setup options in the speaker’s app). This then means that you should add “only” 8.6 m to the actual distance to the loudspeaker.

Of course, if you are using the BeoLab 50 or 90 alone (meaning that there is no video signal, and no other loudspeakers that need time-alignment) then this is irrelevant, and you can just set the Speaker Distance to 0 m. You can also change the loudspeakers to another preset (that you or your installer set up) that uses the High Latency mode for best performance.

Instructions on how to do this are found in the Technical Sound Guide for the BeoLab 50 or the BeoLab 90 via the Bang & Olufsen website at www.bang-olufsen.com.

* Here a “B&O Television” means a BeoPlay V1, BeoVision 11, 14, Avant, Avant NG, Horizon, or Eclipse. Older B&O televisions are different… This will be discussed in the next blog posting.

B&O Tech: Distance Tweaking

#75 in a series of articles about the technology behind Bang & Olufsen loudspeakers

So, you’ve just installed a pair of loudspeakers, or a multichannel surround system. If you’re a normal person then you have not set up your system following the recommendations stated in the International Telecommunications Union’s document “Rec. ITU-R BS.775-1: MULTICHANNEL STEREOPHONIC SOUND SYSTEM WITH AND WITHOUT ACCOMPANYING PICTURE”. That document states that, in a best case, you should use a loudspeaker placement as is shown below in Figure 1.

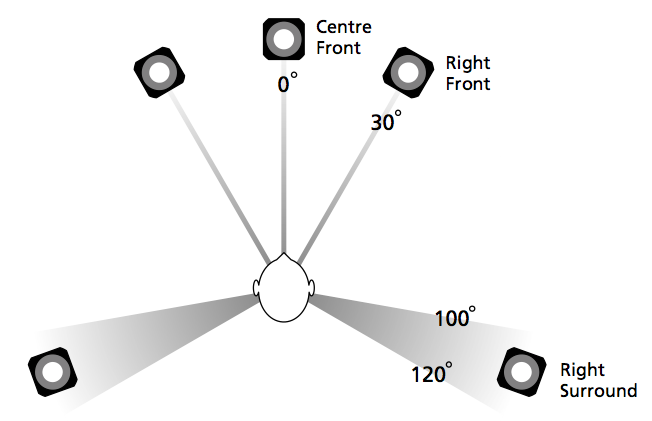
Fig 1. The “ITU 775” recommendation for a 5-channel loudspeaker configuration. All loudspeaker should be matched, and be the same distance from the listening position at the angles shown in the figure.

In a typical configuration, the loudspeakers are NOT the same distance from the listening position – and this is a BIG problem if you’re worried about the accuracy of phantom image placement. Why is this? Well, let’s back up a little…

Localisation in the Real World

Let’s say that you and I were standing out in the middle of a snow-covered frozen pond on a quiet winter day. I stand some distance away from you and we have a conversation. When I’m doing the talking, the sound of my voice leaves my mouth and moves towards you.

If I’m directly in front of you, then the sound (in theory) arrives at both of your ears simultaneously (resulting in an Interaural Time Difference or ITD of 0 ms) and at exactly the same level (resulting in an Interaural Amplitude Difference or IAD of 0 dB). Your brain detects that the ITD is 0 ms and the IAD is 0 dB, and decides that I must be directly in front of you (or directly behind you, or above you – at least I must be somewhere on your sagittal plane…)

If I move slightly to your left, then two things happen, generally speaking. Firstly, the sound of my voice arrives at your left ear before your right ear because it’s closer to me. Secondly, the sound of my voice is generally louder in your left ear than in your right ear, not only because it’s closer, but (mostly) because your head shadows your right ear from the sound of my voice. So, you brain detects that my voice is earlier and louder in your left ear, so I must be somewhere on your left.

Of course, there are many other, smaller cues that tell you where the sound is coming from exactly – but we don’t need to get into those details today.

There are two important thing to note here. The first is that these two principal cues – the ITD and the IAD – are not equally important. If they got in a fight, the ITD would win. If a sound arrived at your left ear earlier, but was louder in your right ear, it would have to be a LOT louder in the right ear to convince you that you should ignore the ITD information…

The second thing is that the time differences we’re talking about are very very small. If I were directly to one side of you, looking directly at your left ear, say… then the sound would arrive at your right ear approximately only 700 µs – that’s 700 millionths of a second or 0.0007 seconds later than at your left ear.

So, the moral of this story so far is that we are very sensitive to differences in the time of arrival of a sound at our two ears.

Localisation in a reproduced world

Now go back to the same snow-covered frozen lake with a pair of loudspeakers instead of bringing me along, and set them up in a standard stereo configuration, where the listening position and the two loudspeakers form an equilateral triangle. This means that when you sit and listen to the signals coming out of the loudspeakers

the two loudspeakers are the same distance from the listening position, and
the left loudspeaker is 30º to the left of front-centre, and the right loudspeaker is 30º to the right of front-centre.

Have a seat and we’ll play some sound. To start, we’ll play the same sound in both loudspeakers at exactly the same time, and at exactly the same level. Initially, the sound from the left loudspeaker will reach your left ear, and the sound from the right loudspeaker reaches your right ear. A very short time later the sound from the left loudspeaker reaches your right ear and the sound from the right loudspeaker reaches your left ear (this effect is called Interaural Crosstalk – but that’s not important). After this, nothing happens, because you are sitting in the middle of a frozen lake covered in snow – so there are no reflections from anything.

Since the sounds in the two loudspeakers are identical, then the sounds in your ears are also identical to each other. And, just as is the case in real-life, if the sounds in your two ears are identical, you’ll localise the sound source as coming from somewhere on your sagittal plane. Due to some other details in the localisation cues that we’re not talking about here, chances are that you’ll hear the sound as originating from a position directly in front of you – between the two loudspeakers.

Because the apparent location of that sound is a position where there is no loudspeaker, it’e like a ghost – so it’s called a “phantom centre” image.

That’s the centre image, but how do we move the image slightly to one side or the other? It’s actually really easy – we just need to remember the effects of ITD and IAD, and do something similar.

So, if I play a sound out of both loudspeakers at exactly the same time, but I make one loudspeaker slightly louder than the other, then the phantom image will appear to come from a position that is closer to the louder loudspeaker. So, if the right channel is louder than the left channel, then the image appears to come from somewhere on the right. Eventually, if the right loudspeaker is louder enough (about 15 dB, give or take), then the image will appear to be in that loudspeaker.

Similarly, if I were to keep the levels of the two loudspeakers identical, but I were to play the sound out of the right loudspeaker a little earlier instead, then the phantom image will also move towards the earlier loudspeaker.

There have been many studies done to find out exactly what apparent phantom image position results from exactly what level or delay difference between the two loudspeakers (or a combination of the two). One of the first ones was done by Gert Simonsen in 1983, in which he found the following results.

[table]

Image Position, Amplitude difference, Time difference

0º, 0.0 dB, 0.0 ms

10º, 2.5 dB, 0.2 ms

20º, 5.5 dB, 0.44 ms

30º, 15.0 dB, 1.12 ms

[/table]

Note that this test was done with loudspeakers at ±30º – so the bottom line of the table means “in one of the loudspeakers”. Also, I have to be clear that the values in this table are NOT to be used concurrently. So, this shows the values that are needed to produce the desired phantom image location using EITHER amplitude differences OR time differences.

Again, the same two important points apply.

Firstly, the time differences are a more “powerful” cue than the amplitude differences. In other words, if the left loudspeaker is earlier, but the right loudspeaker is louder, you’ll hear the phantom image location towards the left, unless the right loudspeaker is a LOT louder.

Secondly, you are VERY sensitive to time differences. The left loudspeaker only needs to be 1.12 ms earlier than the right loudspeaker in order for the phantom image to move all the way into that loudspeaker. That’s equivalent to the left loudspeaker being about 38.5 cm closer than the right loudspeaker (because the speed of sound is about 344 m/s (depending on the temperature) and 0.00112 * 344 = 0.385 m).

Those last two paragraphs were the “punch line” – if the distances to the loudspeakers are NOT the same, then, unless you do something about it, you’ll wind up hearing your phantom images pulling towards the closer loudspeaker. And it doesn’t take much of an error in distance to produce a big effect.

Whaddya gonna do about it?

Almost every surround processor and Audio Video Receiver in the world gives you the option of entering the Speaker Distances in a menu somewhere. There are two possible reasons for this.

The first is not so important – it’s to align the sound at the listening position with the video. If you’re sitting 3 m from the loudspeakers and the TV, then the sound arrives 8.7 ms after you see the picture (the same is true if you are listening to a person speaking 3 m away from you). To eliminate this delay, the loudspeakers could produce the sound 8.7 ms too early, and the sound would reach you at the same time as you see the video. As I said, however, this is not a problem to lose much sleep over, unless you sit VERY far away from your television.

The second reason is very important, as we’ve already seen. If, as we established at the start of this posting, you’re a normal person, then your loudspeakers are not all the same distance from the listening position. This means that you should apply a delay to the closer loudspeaker(s) to get them to “wait” for the sound as it travels towards you from the further loudspeakers. That way, if you have the same sound in all channels at the same time, then the loudspeaker do NOT produce it at the same time, but it arrives at the listening position simultaneously, as it should.

Problem solved! Right?

Wrong.

Corrections that need correcting

Let’s make a configuration of a pair of loudspeakers and a listening position that is obviously wrong.

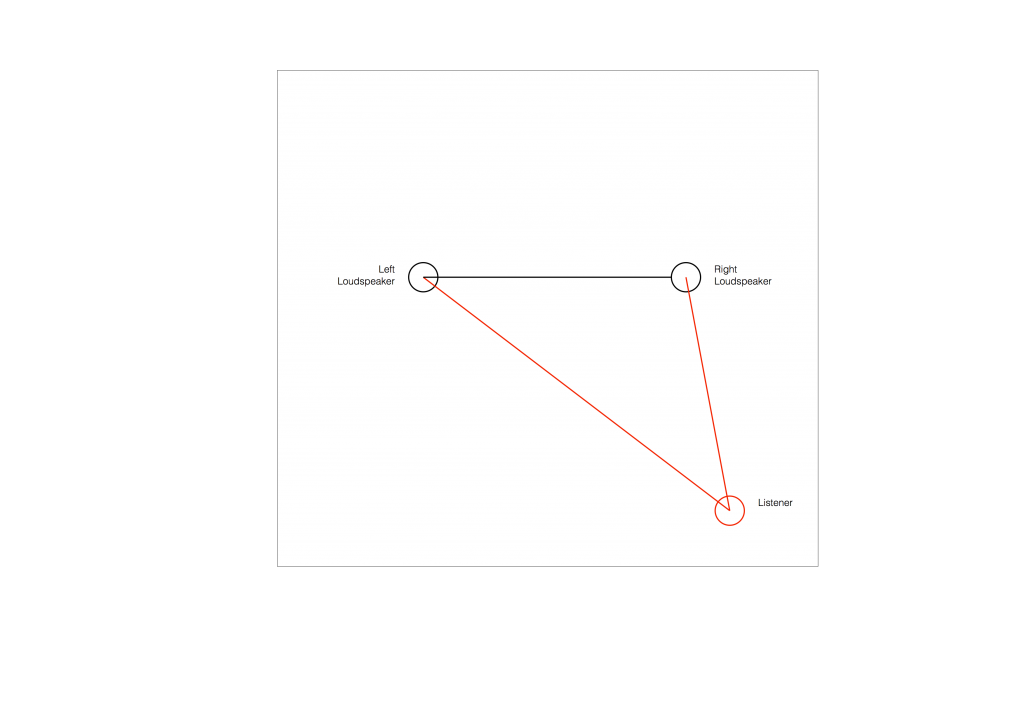
Fig 2. A stereo pair of loudspeakers and a listening position that is no where near the correct location. Notice that the right loudspeaker is much closer than the left.

Figure 2 shows the example of a very bad loudspeaker configuration for stereo listening. (I’m keeping things restricted to two channels to keep things simple – but multichannel is the same…) The right loudspeaker is much closer than the left loudspeaker, so all phantom images will appear to “bunch together” into the right loudspeaker.

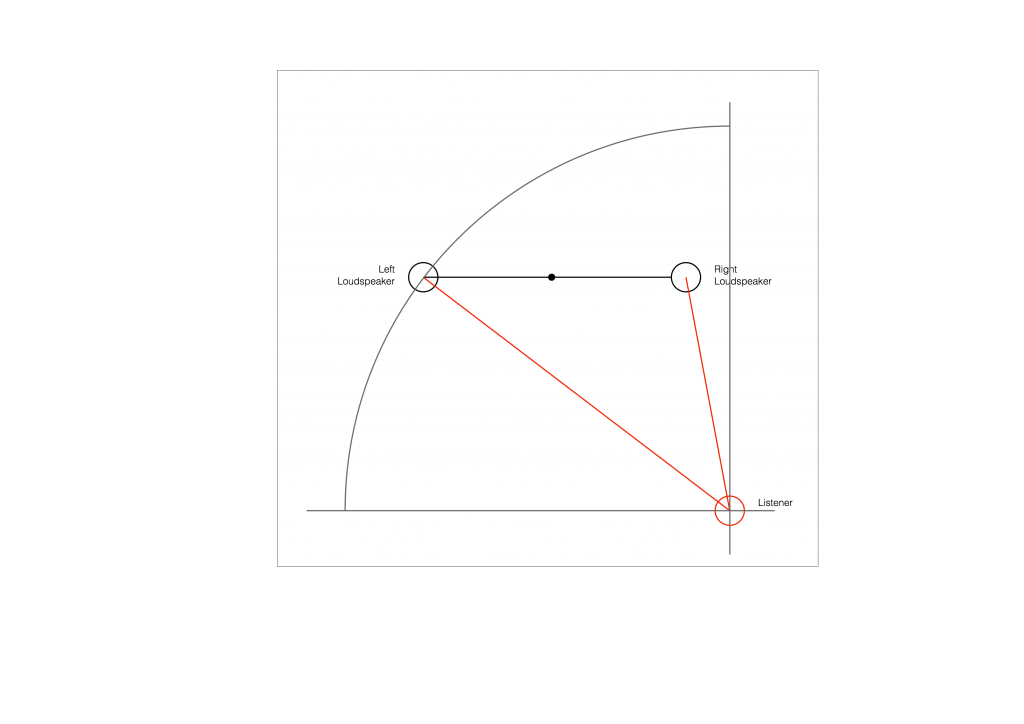
Fig 4. Measuring the distance to the furthest loudspeaker from the listening position

So, to do the correction, you measure the distances to the two loudspeakers from the listening position and enter those two values into the surround processor. It then subtracts the smaller distance from the larger distance, converts that to a delay time, and delays the closer loudspeaker by that amount to compensate for the difference.

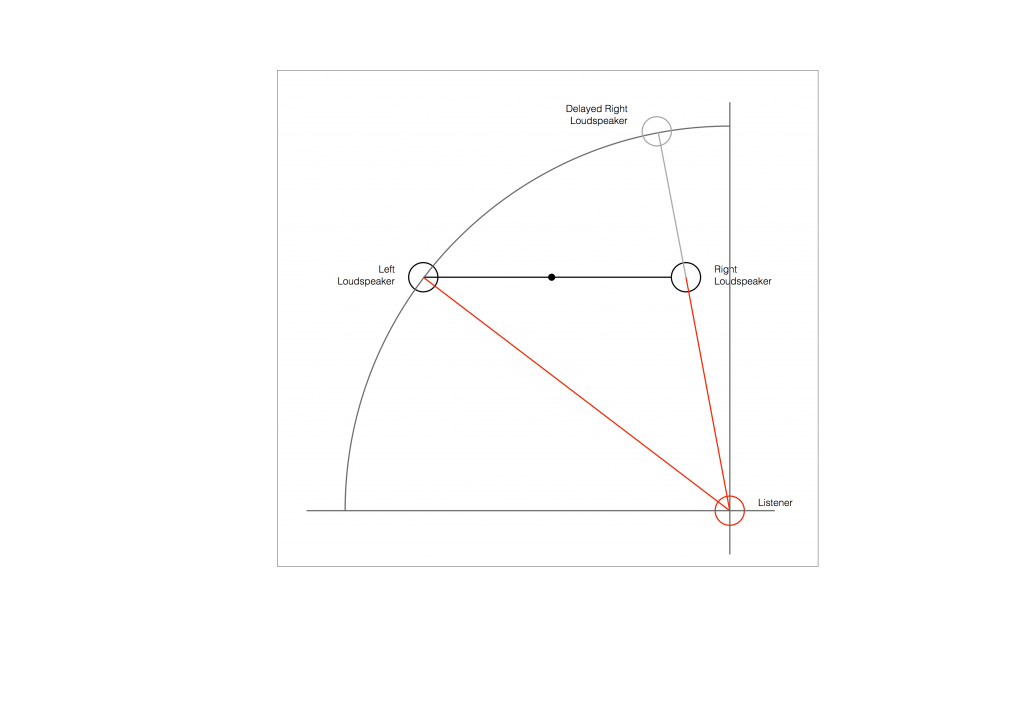
Fig 5. The gray circle shows the apparent position of the right loudspeaker, after a delay has been applied to it, assuming that there are no other cues (such as level or reflections in the room) to tell you where it is.

So, after the delay is applied to the closer loudspeaker, in theory, you have a stereo pair of loudspeakers that are equidistant from the listening position. This means that, instead of hearing (for example) the phantom centre images in the closer loudspeaker, you’ll hear it as being positioned at the centre point between the distant loudspeaker (the left one, in this example) and the “virtual” one (the right one in this example). This is shown below.

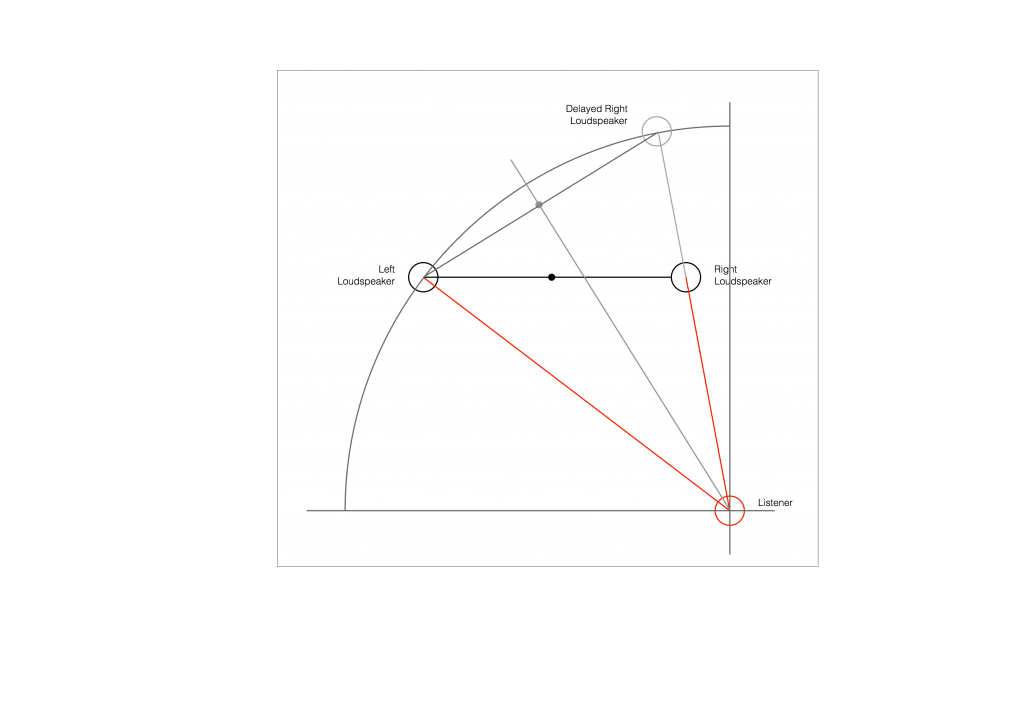
Fig 6. The small grey dot shows the theoretical position of the resulting phantom centre after the two loudspeakers have been time-aligned using delays based on distance to the listening position.

As you can see in Figure 6, the resulting phantom image is at the centre point between the two resulting loudspeakers. But, if you look not-too-carefully-at-all, then you can see that the angle from the listening position to that centre point is not the same angle as the centre point between the two REAL loudspeakers (the black dot).

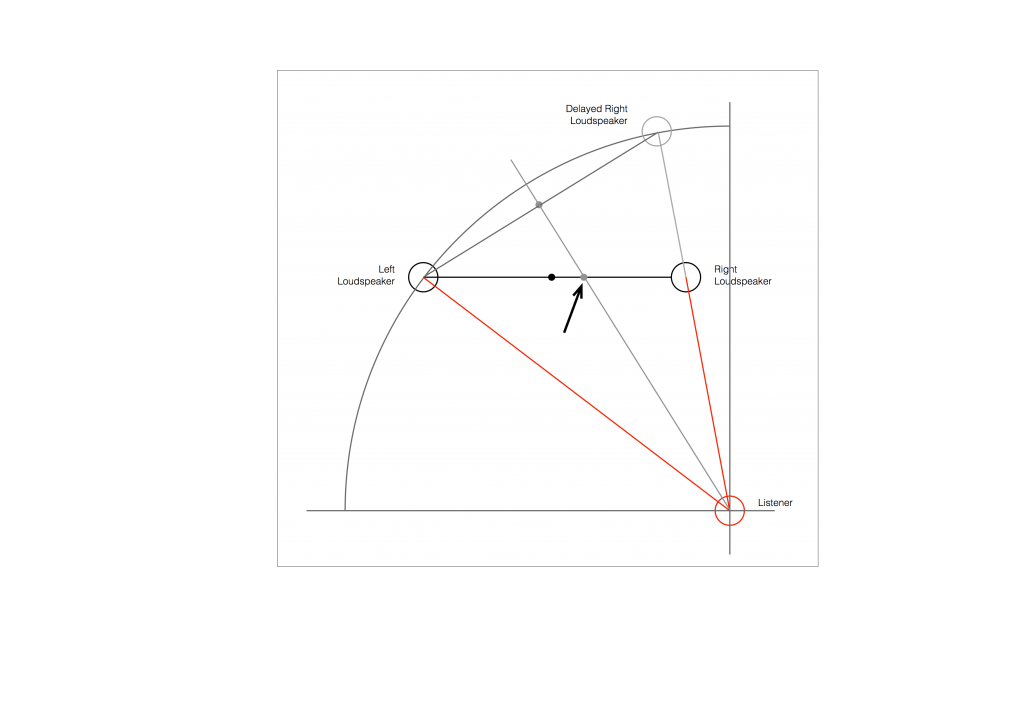
Fig 7. Notice that the corrected phantom image location (indicated by the arrow) is not the same as the desired phantom centre. (which might be, for example, the centre of a television…)

So, this means that, if you use distances ONLY to time-align two (or more) loudspeakers, then your correction till not be perfect. And, the more incorrect your actual loudspeaker configuration, the more incorrect the correction will be.

How do I fix it?

Notice that, after “correction”, the phantom image is still pulling towards the closer loudspeaker.

As we saw above, in order to push a phantom centre image towards a loudspeaker, you have to make the sound in that loudspeaker earlier.

So, what we need to do, after the distance-based time alignment is done, is to force the more distant loudspeaker to be a little earlier than the closer one. That will pull the phantom image towards it.

In order to use a distance compensation to make a loudspeaker produce the sound earlier, we have to tell the processor that it’s further away than it actually is. This makes the processor “think” that it needs to send the sound out early to compensate for the extra propagation delay caused by the distance.

So, to make the further loudspeaker a little early relative to the other loudspeaker, we either have to tell the processor that it’s further away from the listening position than it really is, or we reduce the reported distance to the closer loudspeaker to delay it a little more.

This means that, in the example shown in Figure 7, above, we should add a little to the distance to the left loudspeaker before entering the value in the menus, or subtract a little from the distance to the right loudspeaker instead.

How much is enough?

You might, at this point, be asking yourself “Why can’t this be done automatically? It’s just a little trigonometry, after all…”

If things were as simple as I’ve described here, then you’d be right – the math that is converting distance compensation to audio delays could include this offset, and everything would be fine.

The problem is that I’ve over-simplified a little on the way through. For example, not everyone hears exactly a 10º shift in phantom image with a 2.5 dB inter-channel amplitude difference. Those numbers are the average of a listening test with a number of subjects. Also, when other researchers have done the same test, they get slightly different results. (see this page for information).

Also, the directivity of the loudspeaker will have an influence (that is likely going to be frequency-dependent). So, if you’ve “toed in” your loudspeakers, then (in the example above) the further one will be “aimed” at you better than the closer one, which will have an influence on the perceived location of the phantom centre.

So, the only way to really do the final “tweaking” or “fine tuning” of the distance-compensation delays is to do it by listening.

Normally, I start by entering the distances correctly. Then, while sitting in the listening position, I use a monophonic track (Suzanne Vega singing “Tom’s Diner” works well) and I increase the distance in the surround processor’s menu of the loudspeaker that I want to pull the image towards. In other words, if the phantom centre appears to be located too far to the left, I “lie” to the surround processor and tell it that the right loudspeaker is further by 10 cm. I keep adding distance until the image is moved to the correct location.

B&O Tech: It’s not just a soundbar

#74 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Bang & Olufsen recently released its latest television called BeoVision Eclipse. If you look around the web for comments and reviews, one of the things you’ll come across is that many people are calling it a “soundbar” which is only partly true, which is why B&O calls is a SoundCenter instead.

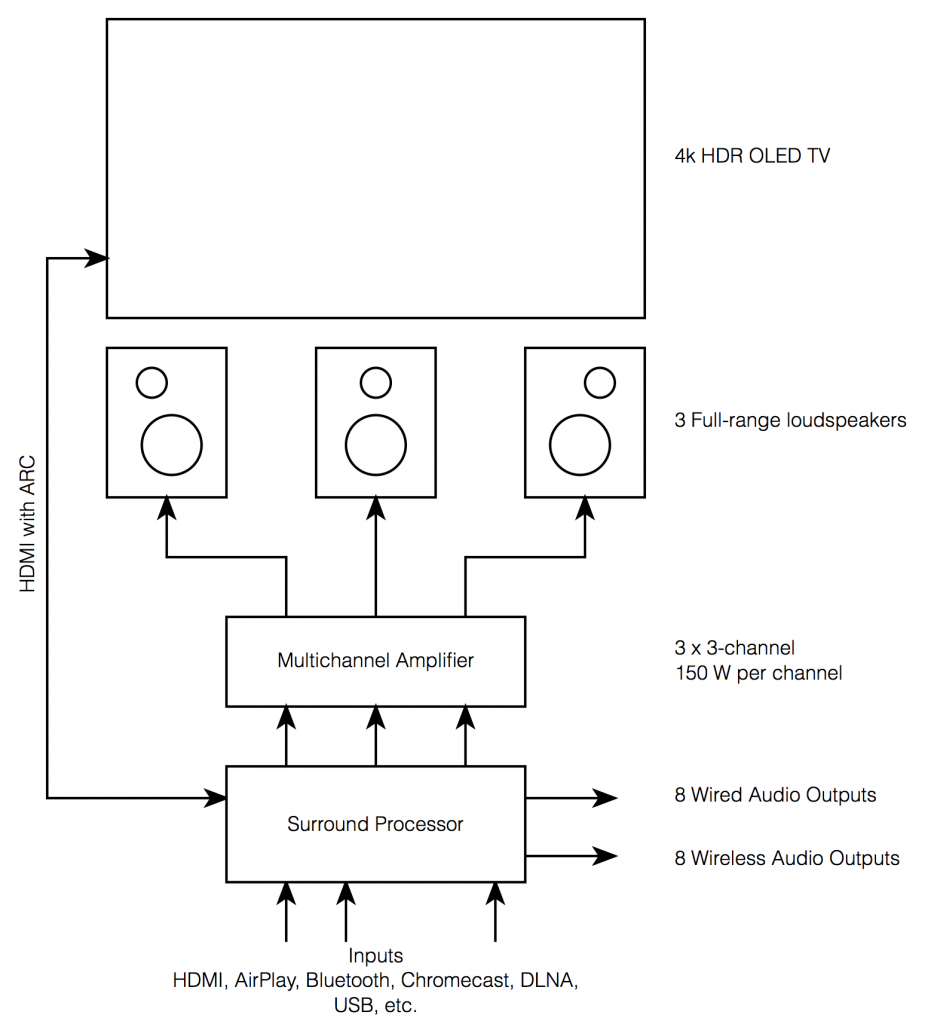
In order to explain the difference, let’s start by looking at what basic components you would need to buy in order to have the equivalent capabilities of the Eclipse.

4K HDR OLED screen
Multichannel audio
- Surround processor + Three-channel amplifier with 150 watts per channel OR
- Audio-Video Receiver (AVR) with 150 watts per channel
- 19 discrete audio output channels
- 1- to 16.5- up/down mixing, dynamic with signal
- User-configurable dynamic output routing
- Intelligent Bass Management
Three full-range loudspeakers
DLNA, Streaming, and multiroom compatible

This is shown in the block diagram in Figure 1 – and it’s important to note that this just an overview of the capabilities – not a thorough list.

Fig 1. An overview of the basic components you would need to buy to get an equivalent of a BeoVision Eclipse.

I’m from the acoustics department, so I’m not going to talk about the video portion of the Eclipse – it’s best to stick with what I know…

Built-in loudspeakers

From the outside, the Eclipse obviously has 3 woofers, each driven by its own 100 W amplifier as well as 2 full range drivers and a tweeter, each of which is individually powered by its own 50 W amplifier. Those 6 amplifiers are each fed by its own Digital to Analogue Converter (or DAC).

The total result of this is a discrete 3-channel loudspeaker array (which some might label a “soundbar”) that is fully-active, and with all processing (such as crossovers, filtering, and ABL, as described in this posting) performed in the Digital Signal Processing (or DSP).

When it leaves the factory, those three channels are preset to act as the Left Front (Lf), Centre Front (Cf), and Right Front (Rf) audio channels, however, these can be changed by the user, as I’ll describe below.

External loudspeakers

The BeoVision Eclipse, like all other current BeoVision televisions includes both wired and wireless outputs for connection to external loudspeakers for customers who either want to have a larger multichannel system, or wish to have the option to upgrade to one in the future.

The Eclipse has 8 wired outputs (on 4 Power Link connections – each of which has 2 discrete audio channels) and 8 wireless outputs (using Wireless Power Link).

This means that, in total, you can have up to 19 loudspeakers delivering signals in a large multichannel surround system (8 wired + 8 wireless + 3 internal). However, even if you have all of those loudspeakers connected, you don’t have to use all of them all of the time…

Audio signal processing

There are many Surround Processors and Audio-Video Receivers (or AVR’s) in the world. These have the primary job of receiving a signal (say, from an HDMI input) and decoding it, splitting it up into the video and audio outputs. The audio channels in the signal are then sent to the appropriate output. However, with almost all Surround Processors and AVRs, the output channel routing is fixed. In other words, the left surround output of the AVR always goes to the same loudspeaker, in the left surround position.

In a Bang & Olufsen television like the BeoVision Eclipse, this routing is not fixed. So, for example, if you connect two extra external loudspeakers, you might choose to use them as the Left Surround (Ls) and Right Surround (Rs) outputs, with the three internal loudspeakers providing the Lf, Cf, and Rf channels. This is shown in Figure 2.

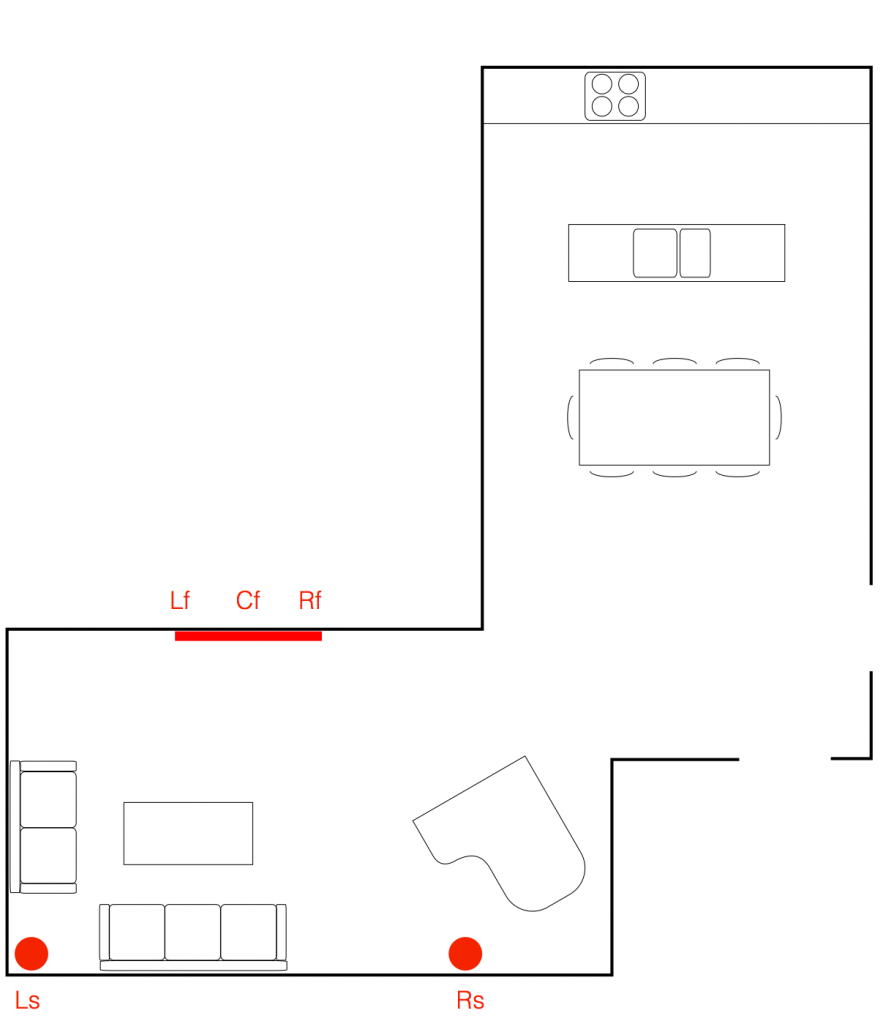
Fig 2. An example of a 5-channel surround system made with a BeoVision Eclipse, providing the front three channels, and two external loudspeakers acting as the Left and Right Surrounds.

This configuration would be saved as a “Speaker Preset” and labelled as you wish (for example, “surround sound”) and even set as a default configuration for the inputs that you wish (the Blu-ray player, for example).

However, you aren’t stuck with this setup. Let’s say, for example, that, when you have dinner, you would like to use the external loudspeakers ONLY as a stereo pair, as is shown below in Figure 3.

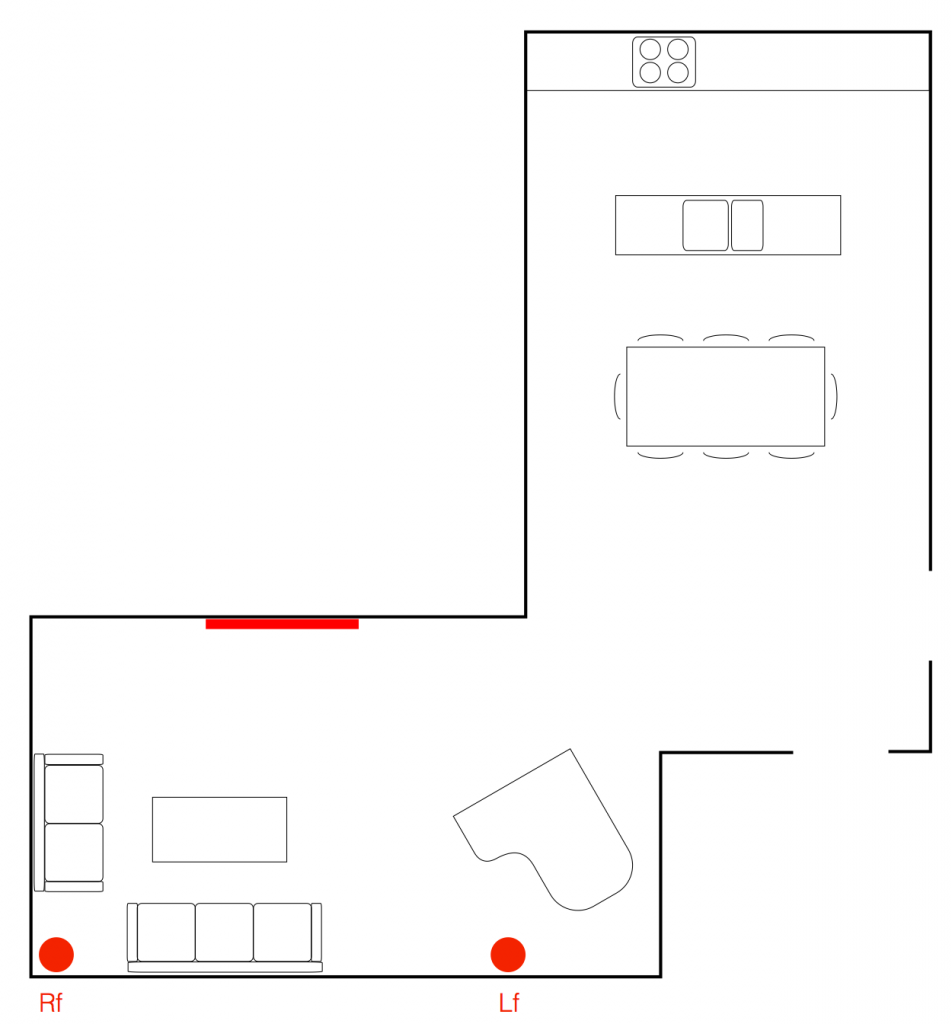
Fig 3. The same system, reconfigured to act as a stereo pair for background music while dining.

Now, the external loudspeakers have changed their Speaker Roles. They were Left Surround and Right Surround in Figure 2 – but now they’re Right Front and Left Front. This configuration can be saved as another Speaker Group, and labelled something like “Dinner Music” for example.

You could also do something completely non-intuitive – for example a configuration for watching the evening news, where you only need to hear the dialogue, but everyone else in the house is either asleep, or not interested in current affairs. Then you can route the Centre Front channel to the closet loudspeaker only, as shown below in Figure 4.

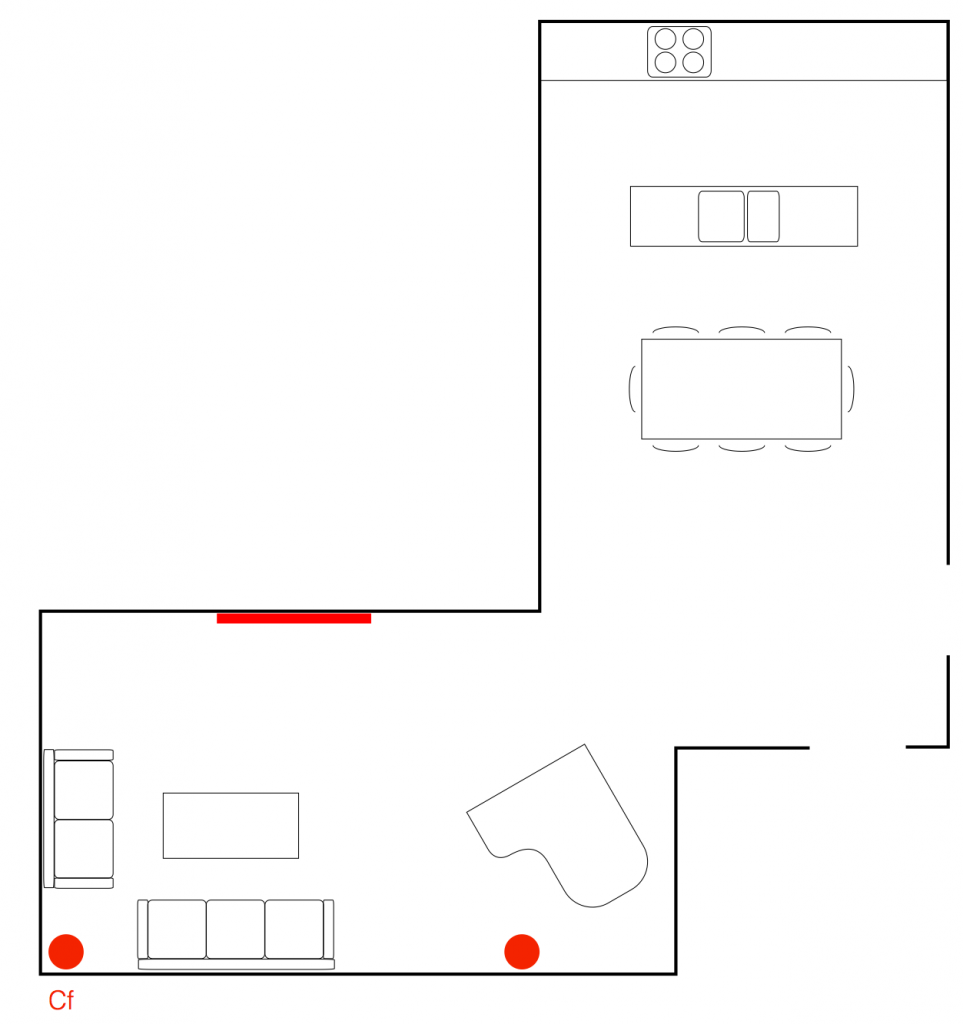
Fig 4. A non-intuitive Speaker Group for listening to late-night evening news without disturbing the rest of the house.

This can be saved as another Speaker Group, called “Speech – Night Listening” for example.

It should also be noted that there are no rules applied to the distribution of Speaker Roles in a Speaker Group. So, for example, if you wanted to have 19 loudspeakers, all playing the Left Surround channel, the TV will let you do this. I’m not suggesting that this is a good idea – I’m merely saying that the TV will not stop you from doing this…

Of course, when you create a Speaker Group, you not only define the various roles of the loudspeakers, you also set their Speaker Levels and Speaker Distances to ensure that the levels and time-of-arrivals are all aligned as you require for your configuration.

Update: I just made a new Speaker Group on a system with a BeoVision Eclipse and a pair of BeoLab 90’s that I thought might make an interesting addition to this section. The Eclipse Speaker Group was created such that all connected loudspeakers (internal and external) were set to have a Speaker Role of NONE. This basically means that the TV uses no loudspeakers. You may wonder why this is a useful Speaker Group. The reason is that I was using the Eclipse as an external monitor for a computer, but I wanted to listen to music from the BeoLab 90’s from another device (which is connected to their S/P-DIF Coaxial input). So, the Eclipse turns off the BeoLab 90’s, which “frees them up” to automatically switch to the S/P-DIF input.

Up-/down-mixing capabilities

Internally, the Eclipse, like the BeoVision 11, Avant, Horizon, and 14, can create up to a 16-channel upmix of all signals that come into it, using the True Image algorithm. However, if your input channel mapping matches your output, then the upmixer does nothing. This decision (whether to upmix, downmix, or do nothing) is continually made on-the-fly. So, for example, let’s say that you have a 5.1-channel loudspeaker configuration with 5 main loudspeakers and one subwoofer. You start by playing 2-channel stereo music from a USB stick and the True Image algorithm will upmix the 2 input channels to your 5 output channels, and also bass mange the low frequency content to the subwoofer. You then switch to watch a DVD with a 5.1-channel signal, and True Image will connect the 6 input channels to the 6 loudspeakers directly without doing any interim spatial processing. Then, you change to a Blu-ray disc with 7.1-channel audio content and True Image will downmix the 8 incoming channels to your 6 loudspeakers.

All of this happens automatically, and is also true if you switch Speaker Groups. So, if you start watching the 5.1-channel DVD with a 5.1-channel Speaker Group, then True Image will pass the signals through. If you then switch to the 2-channel Speaker Group, True Image will automatically start downmixing for you (rather than just not playing the “missing” output channels).

Of course, if you’re a purist, then the True Image algorithm can be disabled, and the incoming audio channels can be just routed to their respective outputs directly. However, this means that if your input format does not match your output format, then either you’ll not hear some audio channels (if you have more input channels than output channels) OR some loudspeakers will not play audio (if you have fewer input channels than output channels).

Intelligent bass management

If all of the external loudspeakers that you’ve connected to the BeoVision Eclipse are Bang & Olufsen products, then you simply tell the television which loudspeaker models you have (if they’re connected wirelessly, then this happens automatically) and the TV will automatically decide whether each loudspeaker should be bass-managed or not. This is because the TV is programmed with the bass capabilities of all Bang & Olufsen loudspeakers in the current portfolio – and many legacy products. This means that the TV “knows” which speakers can play the loudest bass – so it will automatically configure itself for each Speaker Group, ensuring that your bass is re-routed to the most capable loudspeakers.

Of course, this can be over-ridden in the user menus. So, if you wish to disable Bass Management, you can do so. However, you can also create extreme cases where you send the bass managed signal to all loudspeakers. This is not necessarily a good idea – nor will it necessarily give you the most bass (due to possible phase differences between the loudspeakers, for example) – however, you can do it if you wish.

If the external loudspeakers are not Bang & Olufsen products, then you simply choose “Other” as your Speaker Connection (or speaker type) in the menus, and the TV will know that it cannot make automatic decisions about the bass management – so you’ll have to configure this yourself.

Automatic Latency Management

Different Bang & Olufsen loudspeakers have different “latencies”. (The latency of a loudspeaker is the time it takes for the signal to go through it – from the electrical input to the acoustical output.) For some older products (like the BeoLab 3, for example) then the latency is 0 ms, because it is an analogue loudspeaker. For some others, it is between 2.5 and 5 ms (depending on the particular loudspeaker). The BeoLab 50 and BeoLab 90 each have two latency modes: either 25 ms or 100 ms, depending on how they are configured.

In order to ensure that all of these different loudspeakers can “live together” in a single surround system (and also in a multiroom configuration with other products in your house), the TV must also “know” the latencies of the various loudspeakers that are connected to it.

In addition, the BeoVision Eclipse can “tell” the BeoLab 50 and 90 to change latency settings on-the-fly to optimise the configuration to ensure lip sync. (Note that, in order for this to happen, the BeoLab 50 and 90 must be set to “Auto” latency mode, allowing them to be switched by the TV.)

Other Features

As I said at the top, I’m concentrating on the audio and acoustic features of the BeoVision Eclipse. There are many aspects of the LG screen that I won’t discuss here. In addition, there are a multitude of video and audio input options and built-in sources (like Netflix, Amazon, Google Chromecast, Apple AirPlay, and so on…) which I also won’t go through.

Finally, of course, it goes without saying that in order to control all of this you only need to have one remote control sitting on your coffee table…

For more information

True Image Upmixing

What’s So Great About Active Loudspeakers?

B&O Tech: Directivity and Reflections

#73 in a series of articles about the technology behind Bang & Olufsen loudspeakers

The setup

Let’s start by inventing a loudspeaker. It has a perfectly flat on-axis response in a free field. This means that if you send a signal into it, then it doesn’t cause any particular frequency to sound louder or quieter than the others when you measure it in an infinite space that is free of reflections.

We’ll also say that it has a perfectly omnidirectional directivity. This means that the loudspeaker has the same behaviour in all directions – there is no “front” or “back” – sound goes everywhere identically.

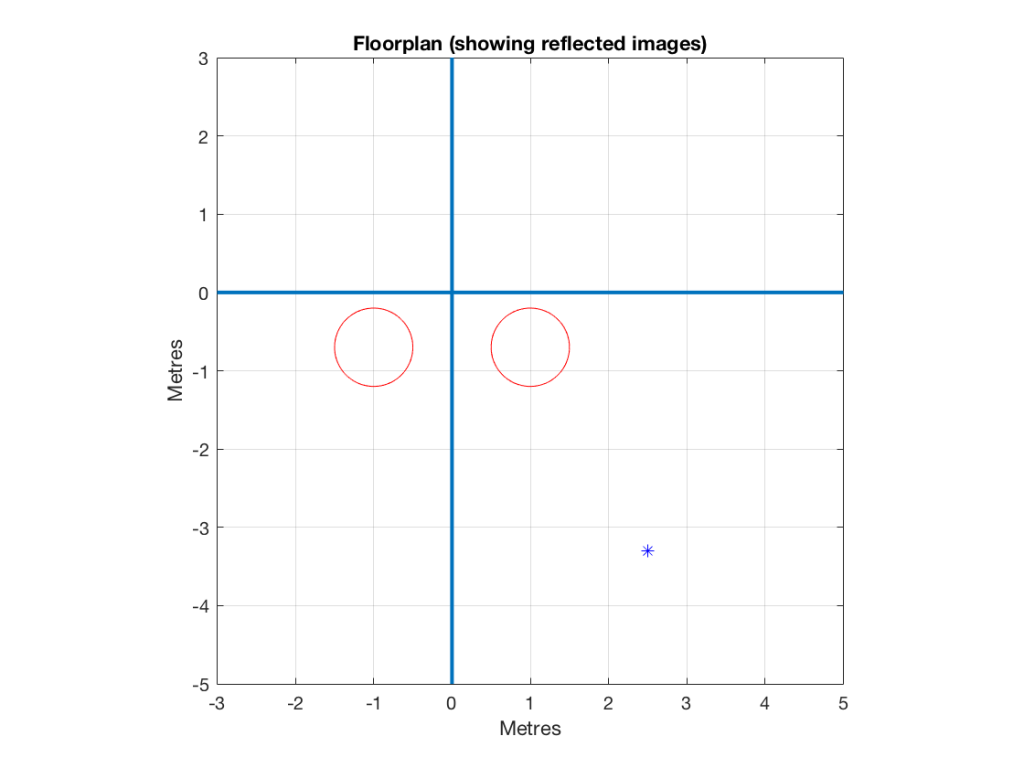
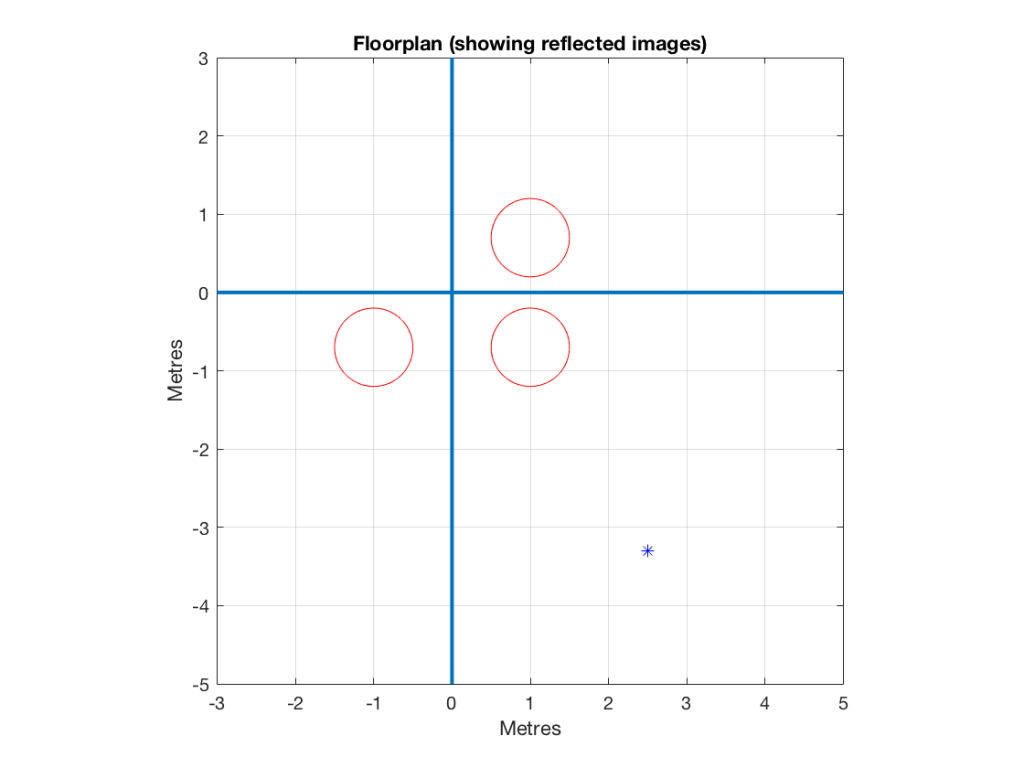
Let’s then put that loudspeaker in a strange room that has only two walls – the left wall and the front wall – and these extend to infinity. We’ll put the loudspeaker, say 1 m from the left wall and 70 cm from the front wall. These are completely arbitrary values, but they’re not weird… Finally, we’ll sit 3 m away from the loudspeaker, as if we were set up to listen to it as the left front loudspeaker in a stereo pair.

A floorpan of that setup is shown below in Figure 1.

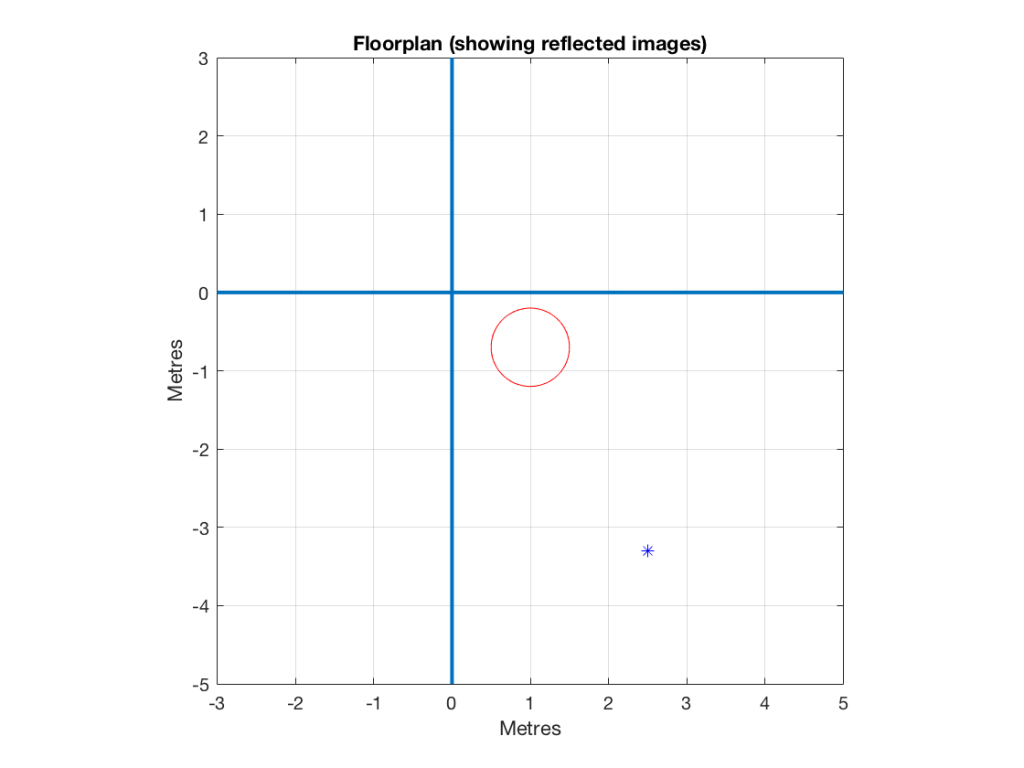
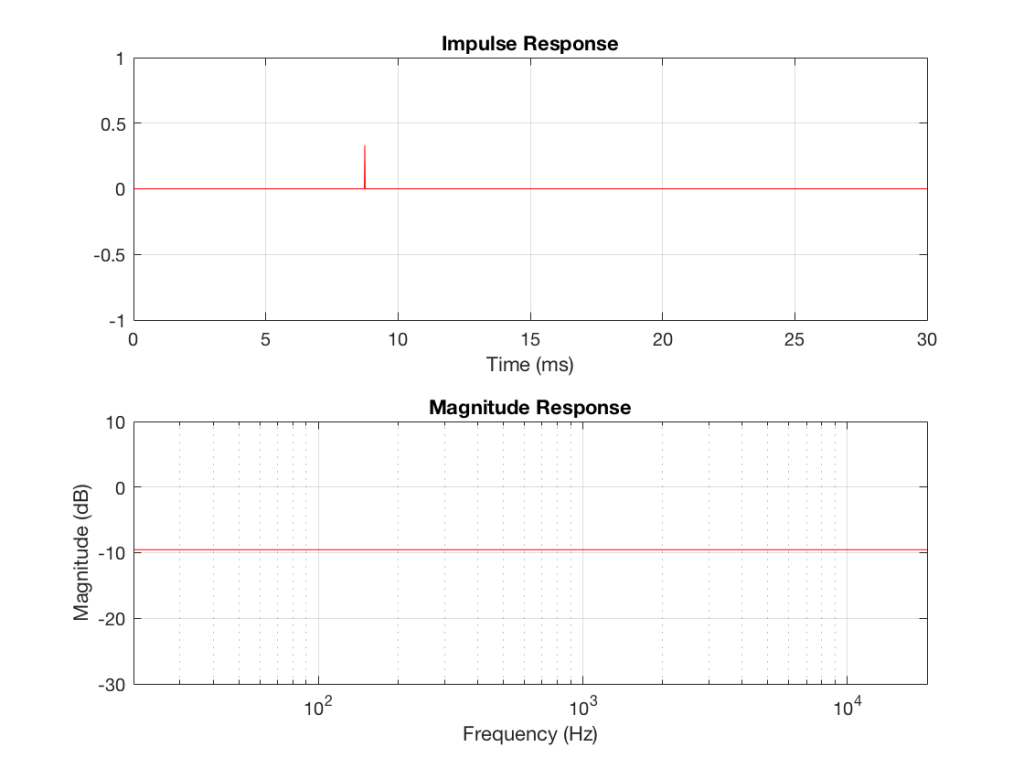
Fig 01: The centre of the red circle shows the location of the loudspeaker, and the circle itself represents the fact that the loudspeaker is omnidirectional. The blue lines are the walls, and the blue asterisk is the listening position.

If the two walls were completely absorptive, then there would be no energy reflected from them. If we were to replace the loudspeaker with a light bulb, then the equivalent would be to paint the walls flat black so no light would be reflected. In this theoretically perfect case, then the impulse response and the magnitude response of the loudspeaker at the listening position would be the same as in a free field, since there are no reflections. These would look like the plots in Figure 2.

Fig 2. The impulse response and the magnitude response of the arrangement shown in Figure 1. Note that it takes approximately 9 ms for the sound to reach the listening position, and that there are no reflections after that. The magnitude response is completely flat, but has an overall gain of almost -10 dB since it is measured relative to a reference distance of 1 m.

Through the looking glass

Imagine that you’re standing outdoors on a moonless night, and the only things you have with you are a lightbulb (that is magically lit) and a mirror. You’ll be able to see two light bulbs – the real one, and the one that is reflected by the mirror. If there is really no other light and no other objects, then you won’t even know that it’s a mirror, and you’ll just see two light bulbs (unless, of course, you can see yourself as well…)

In 1929, an acoustical physicist working at Bell Laboratories named Carl F. Eyring presented a new idea to the Acoustical Society of America. He was trying to calculate the reverberation time in “dead” rooms by considering that the walls were perfect mirrors, and that instead of thinking of sound sources and reflections, you could just pretend that the walls didn’t exist, and that the reflections were actually just images of other sound sources on the other side of the wall (just like that second light bulb in the example above…)

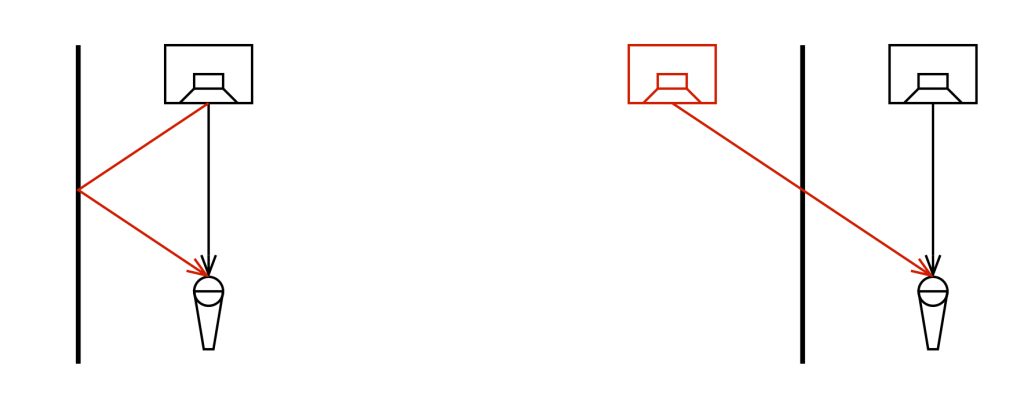
Fig 3: Two conceptual diagrams showing (in a perfect world) identical systems. On the left is the direct sound (the black arrow) and the reflected sound (the red arrow) reaching the microphone. On the right, we see the direct sound coming from the “real” loudspeaker, and the reflection coming from an image of that loudspeaker on the other side of the wall – as if the wall were not there.

This method of simulating and predicting acoustical behaviour in rooms, now called the “image model” has been used by many people over the decades. Eyring published a paper describing it in 1930, but it has since been standard method, both for prediction and acoustical simulation (first proposed by Allen and Berkley in 1979).

The effects of one sidewall reflection

Let’s use the image model to do a very basic prediction of what will happen to our impulse and magnitude responses if we have a single reflection from the left-hand wall.

Fig 4: An image model representation of the same loudspeaker shown in Figure 1, with a perfectly reflective sidewall on the left.

Fig. 5:The Impulse response and magnitude response of the resulting signal at the listening position. Notice that the direct sound is identical to that shown in Figure 2, but now there is an additional reflection that arrives about 5 ms later, and quieter, since the path the reflection takes is longer. The resulting magnitude response is a classic “comb filter”, so-called because it looks like a hair comb if you plot it on a linear frequency scale.

As can be seen in Figure 5, the resulting magnitude response of an omnidirectional loudspeaker with a single, perfect reflection certainly has some noticeable artefacts. If the listening position were closer to the loudspeaker, the artefacts would be smaller, since the reflected signal would be quieter than the direct sound The further away you get, the more the two path lengths are the same, and therefore the bigger the effect on the summed signal.

Of course, this is an unrealistic simulation, since everything is “perfect” – perfect reflection, perfectly omnidirectional loudspeaker with a perfectly flat magnitude response, and so on… However, for the purposes of this posting, that’s good enough.

Let’s now change the directivity of the loudspeaker to alter the balance of level between the direct and the reflected sounds. We’ll make the loudspeaker’s beam width more narrow, giving it the same behaviour as a cardioid microphone (which is called a cardioid because a polar plot of its directivity pattern looks like a heart – cardiovascular and cardioid have the same root).

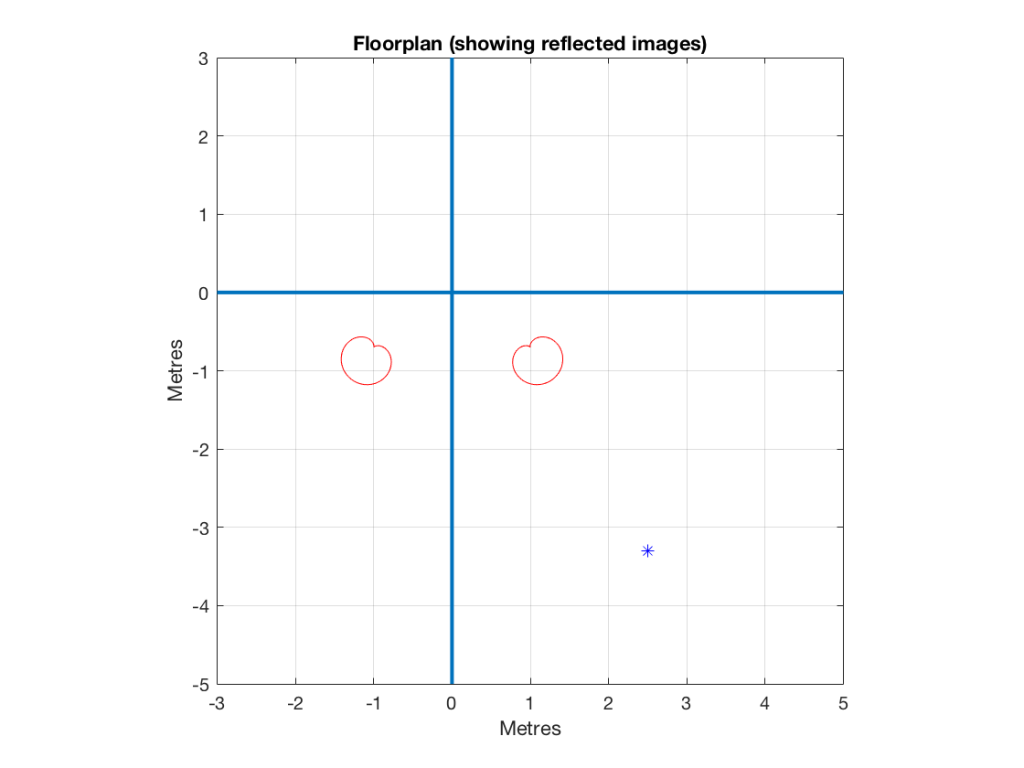
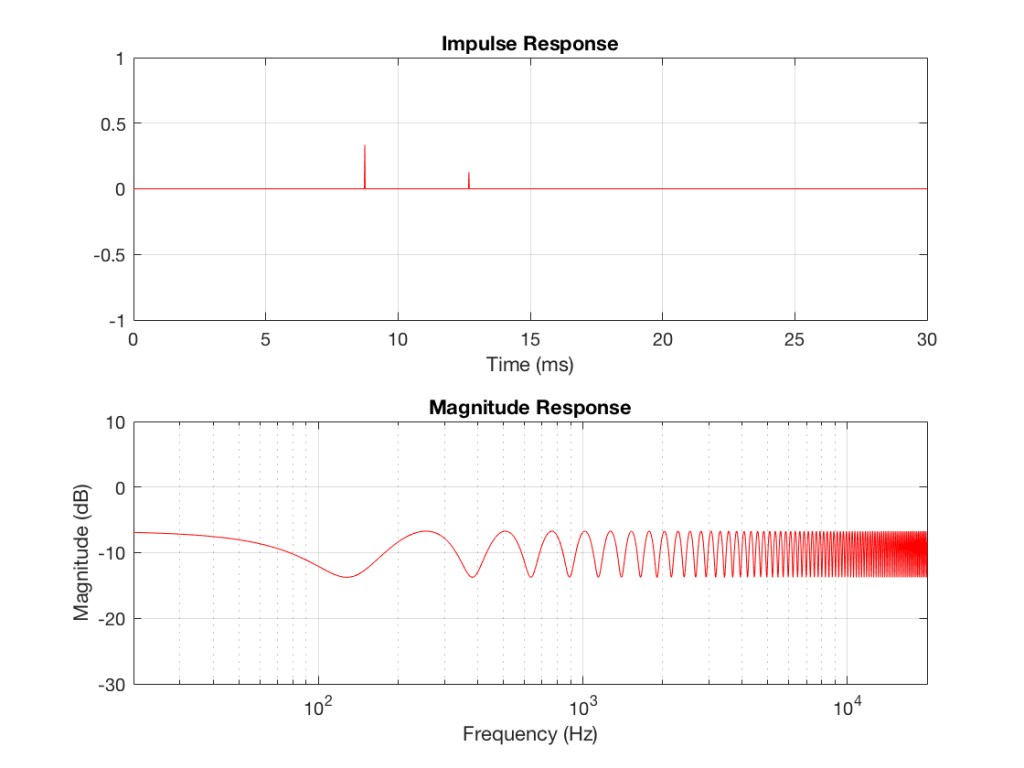
Fig. 6: The same arrangement as shown in Figure 4, but with more directional loudspeakers.

Fig. 7: The impulse and magnitude responses of the arrangement shown in Figure 6.

If you look at Figure 7, you’ll see that the times of arrival of the two signals have not changed, but that the effect of the artefact in the frequency domain is reduced (the peaks and dips are smaller). The frequencies of the peaks and dips are the same as in Figure 5 because those are determined by the delay difference between the two spikes in the impulse response. The peaks and dips are smaller because the reflected sound is quieter (because the image loudspeaker – the reflected signal is beaming in a different direction).

Let’s try a different directivity pattern – a dipole, which has a polar patter than looks like a figure “8”.

Fig 8: A dipole loudspeaker and its image, in the same positions as in Figure 4.

Fig 9: The impulse and magnitude responses of the arrangement shown in Figure 8.

Notice now that, because the listening position is almost perfectly in line with the “null” – the “dead zone” of the reflected loudspeaker, there is almost nothing to reflect. Consequently, there is very little effect on the on-axis magnitude response of the loudspeaker, as can be seen in the magnitude response in Figure 9.

So, the moral of the story so far is that without moving the loudspeaker or the listening position, or changing the wall’s characteristics, the time response and magnitude response of the loudspeaker at the listening position is heavily dependent on the loudspeaker’s directivity.

Two reflections

Let’s continue the experiment, making the front wall reflective as well.

Fig 11. The impulse and magnitude responses at the listening position with two reflections and an omnidirectional loudspeaker, as shown in Figure 10. Note that the second impulse (the first reflection after the direct sound) is the one from the front wall, since that image is closer to the listening position.

Fig 12. An image model representation of two reflections and a loudspeaker with a cardioid directivity.

Fig 13. The artefacts on the magnitude response are considerably less for a cardioid loudspeaker than with an omnidirectional, since, as can be seen, the reflected signals are considerably quieter due to the angle of the listening position with respect to the rotation of the image loudspeakers.

Fig 14: An image model representation of two reflections and a loudspeaker with a dipole directivity.

Fig 15: The artefacts on the magnitude response are different when the loudspeaker is a dipole. Notice that the sidewall reflection is much quieter than the front wall reflection, as we saw already in Figure 9.

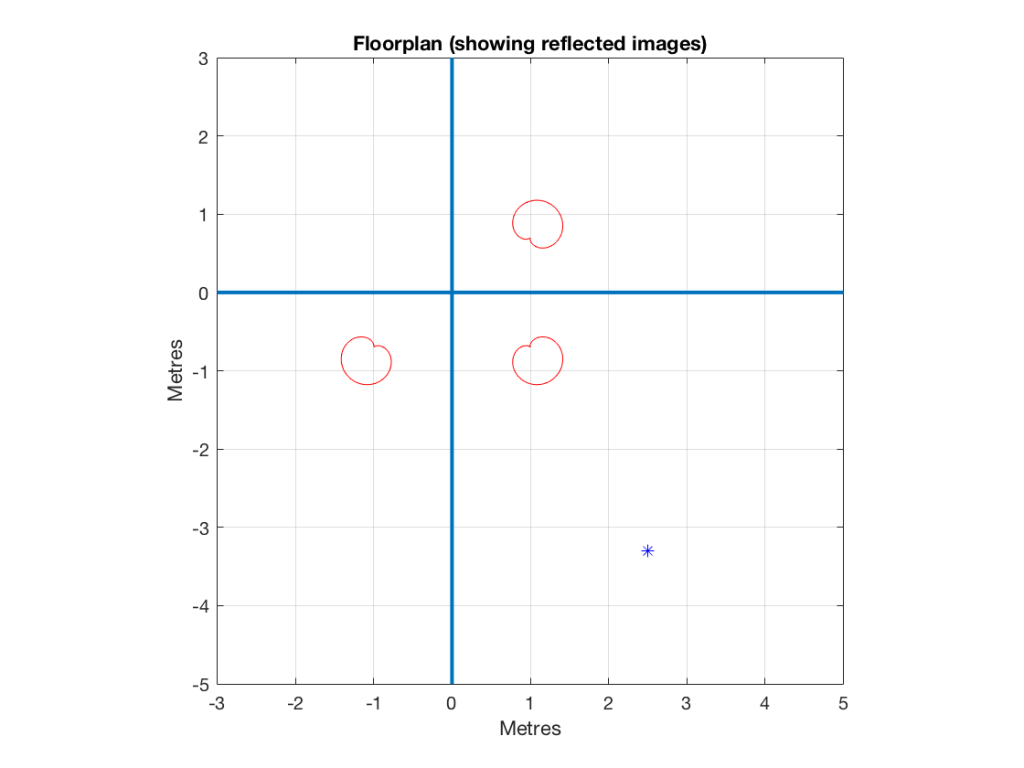
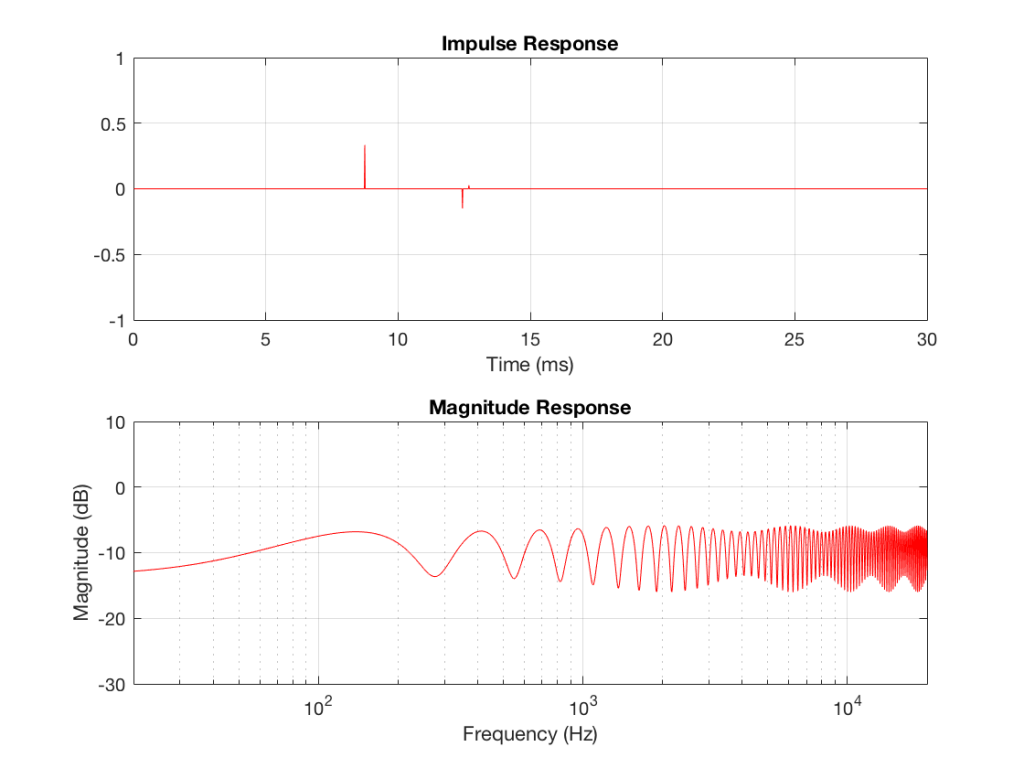
In Figure 15, one additional effect can be seen. Since the reflection off the front wall is negative (in other words, it “pulls” when the direct sound “pushes”) due to the behaviour of the dipole, there is a cancellation in the low frequencies, causing a drop in level in the low end. If we were to push the loudspeaker closer to the front wall, this effect would become more and more obvious.

The moral of the story is…

Of course, this is all very theoretical, however, it should give you an idea of three things.

The first is a simple method of thinking about reflections. You can use the Image Model method to imagine that your walls are mirrors, and you can “see” the other loudspeakers on the other sides of those mirrors. Those images are where your reflections are coming from.

The second is the obvious point – that the summed magnitude response of a loudspeaker’s direct sound, and its reflections is dependent on many things, the directivity being one of them.

The third is possibly the most important. All three of the loudspeaker models I’ve used here have razor-flat on-axis responses in a free field. So, if you were trying to decide which of these three loudspeakers to buy, you’d look at their “frequency response” plots or data and see that all of them are flat to within 0.0001 dB from 1 Hz to infinity Hz, and you’d think that they’d all sound “the same” under the same conditions. However, nothing could be further from the truth. These three loudspeaker with identical on-axis responses will sound completely different. This does not mean that an on-axis magnitude response is useless. It only means that it’s useless in the absence of other information such as the loudspeaker’s power response or its frequency-dependent directivity.

To keep things simple, I have not included frequency-dependent directivity effects. I may do that some day – but beware that it is not enough to say “the loudspeaker beams at higher frequencies so I don’t have to worry about it up there” because that’s not necessarily true – it’s different from loudspeaker to loudspeaker.

This also means that none of the plots I’ve shown here can be used to conclude anything about the real world. All it’s good for is to get a conceptual, intuitive idea of what’s going on when you put a loudspeaker near a wall.

One final comment: the microphone that I’m simulating here has an omnidirectional characteristic. This means that it is as sensitive to the reflected sound as it is to the direct sound, since the angle of incidence of the sound is irrelevant. The way we humans perceive sound is different. We do not perceive the comb filter that the microphone sees when the reflection is coming in from our side, since this is information that is recognised by the brain as being reflected – and it’s used to determine the distance to the sound source. However, if you plug one ear, you may notice that things sound more like you see in the plots, since you lose part of your ability to localise the direction of the signals in the horizontal plane.

For more reading…

Allen, J.B., & Berkley, D.A. (1979) “Image Method for Efficiently Simulating Small-Room Acoustics,” Journal of the Acoustical Society of America, 65(4): 943-950, April.

Eyring, C.F. (1930) “Reverberation Time in ‘Dead’ Rooms,” Journal of the Acoustical Society of America, 1: 217-241.

Gibbs, B.M., & Jones, D.K., (1972) “A Simple Image Method for Calculating the Distribution of Sound Pressure Levels Within an Enclosure,” Acustica, 26: 24-32.

BeoLab 50 Reviews

andreweverard.com

“So how do they sound? Well, after a lengthy listening session in the Struer listening rooms, I had to conclude that these speakers may look (almost) conventional, but they sound anything but. There’s massive bass, seeming unburstable but as tightly controlled as it is extended, and a lovely sense of integration, sweetness and detail in the midband and treble.”

“If the BeoLab 90 saw the company moving back into the audiophile arena, albeit with a speaker whose form-factor was, to say the least, challenging, then the BeoLab 50 may well win it even more fans in the ‘serious audio’ arena, not least due to industrial design making it look like – well, like a pair of speakers.”

parttimeaudiophile.com

“The BeoLab 50 seemed to cope with hotel-room acoustic issues well, too, possibly because of the side-firing woofers and the active room correction. Bass and high frequencies, in particular, were free from boominess, standing waves, cancellations and weird reflections. At the same time, there was an impressive recreation of instrumental sounds on the Vaughan track, both on the initial notes and on reverb trails that drifted far back into the soundstage”

B&O Tech: Signal Mixing and Decomposition

#72 in a series of articles about the technology behind Bang & Olufsen loudspeakers

After a previous posting, someone posted this as part of a comment:

“What I’ve been asking myself for a long time: how does a single driver manage to produce two or more frequencies (or a frequency range) at the exact same time? For example a singer singing while the guitar plays in the background. Could you try to explain how this works?”

So, this posting is an attempt to answer that question.

Adding signals together

Sound is a change of air pressure over time. That pressure is modulating on top of the day’s average barometric pressure – which is just a measurement of how closely the air particles around you are squeezed together. On a high-pressure day, the air is more densely packed – on a low pressure day, the air is less dense.

When you make a sound, you make slight variations in that pressure – so, for example, when a woofer moves out of a loudspeaker enclosure (a fancy name for “box”) then it pushes the air particles in front of it, and they’re squeezed together, resulting in a compression wave that radiates away from the loudspeaker. When the woofer pulls into the enclosure, it pulls the air particles apart, and you get a rarefaction wave instead. (You can see an animation of this at this posting.)

Let’s make a graph that shows a plot of the acoustic pressure changing over time. This is shown below in Figure 1. When this plot shows a positive number, it means that the air particles are being compressed more than normal. When it’s negative, then they’re being separated more than normal. Without getting into too many details, let’s just say that this is a low frequency. (If you want to get picky, then you’ll see that this is one cycle of a wave that takes 100 ms. Since there are 1000 ms in a second, then this must be a 10 Hertz signal, because 1000 / 100 = 10. That makes it a VERY low frequency by normal audio standards… )

Let’s also look at an example of a higher frequency, shown in Figure 2, below.

Figure 2: A signal with a higher frequency and a lower amplitude than the one shown in Figure 1.

We can see that Figure 2 has a higher frequency signal, because it moves up and down more frequently. It has 5 cycles (5 ‘ups’ and ‘downs’) in the same amount of time that it took the wave in Figure 1 to have 1 cycle – therefore it is 5 times the frequency (and therefore, if you’re being picky, 50 Hz – which, by audio standards, is also a very low frequency, but this is just an example…)

Ignoring that ACTUAL frequencies that are plotted there, let’s pretend for a moment that the low frequency (Figure 1) came from a bass guitar and the higher frequency (Figure 2) came from a singer. If we took those two signals and put them into a mixing console, what does the result look like?

Well, we take the instantaneous value of the signal at one moment in time and add it to the instantaneous value of the other signal at the same time. Let’s do that.

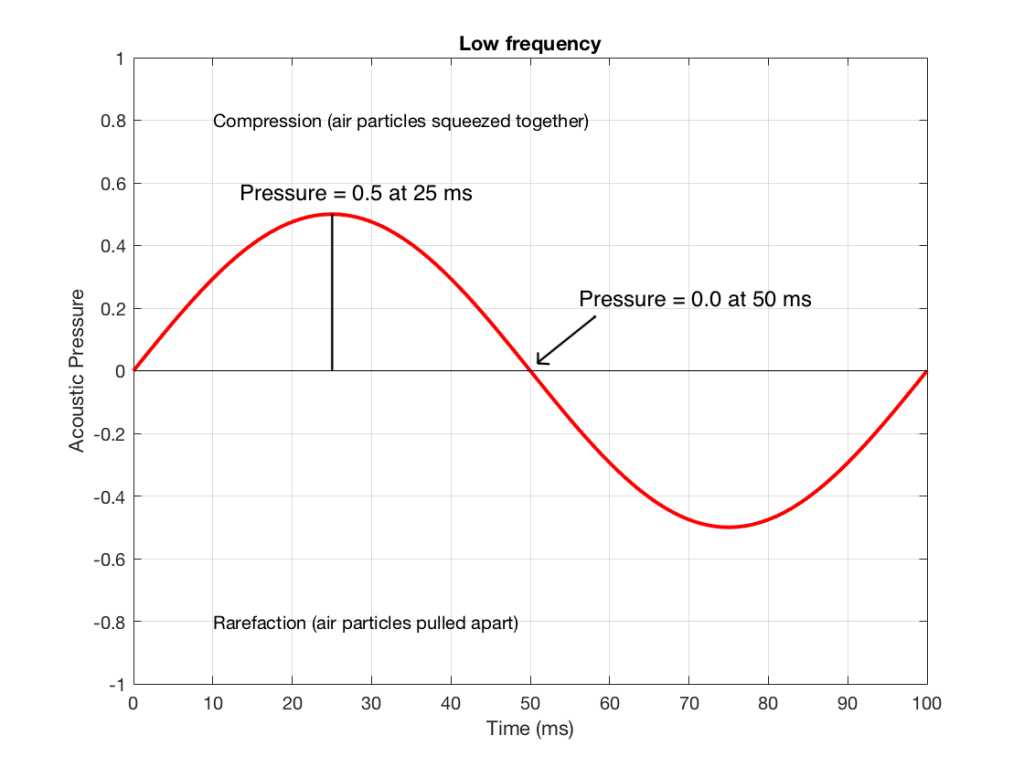
Figure 3: Some details on the signal in Figure 1.

Figure 3 shows the same signal as in Figure 1, but I’ve pointed out the values at two moments in time – at 25 ms and at 50 ms. So, for example, you can see there that, at 25 ms, the value is 0.5 – whatever that means…

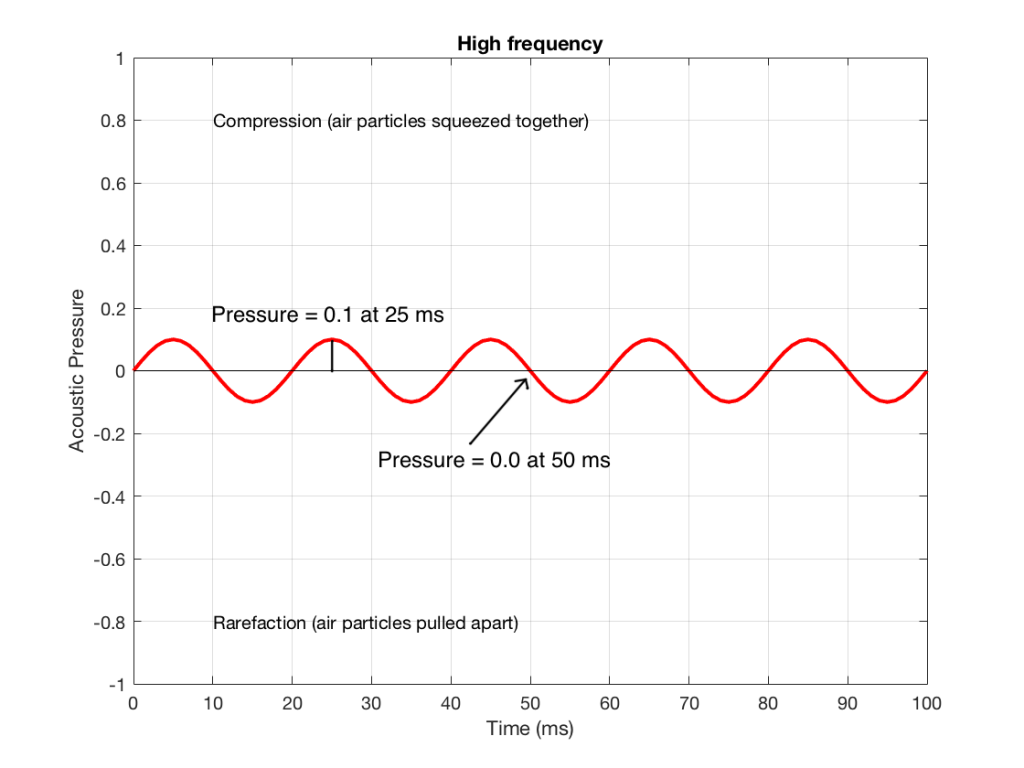
Figure 4: Some details on the signal in Figure 2.

Figure 4 shows the same signal as in Figure 2, but I’ve pointed out the values at two same moments in time – at 25 ms and at 50 ms. So, for example, you can see there that, at 25 ms, the value is 0.1 – whatever that means.

We take the value at 25 ms from each of the two signals (0.5 and 0.1) and add them together to get 0.6. This is the value of the signal at the output of the mixer at 25 ms. At 50 ms, the mixer’s output will have a value of 0 (because 0+0 = 0). This is shown graphically below for all of the values of both plots from 0 ms to 100 ms.

Figure 5: The result of adding Figures 1 and 2.

So, you can see in Figure 5 what the result will be. This signal contains both the low frequency, shown in Figure 1 and the higher frequency shown in Figure 2. If we send this combined signal to a loudspeaker, then both signals will get reproduced.

One interesting thing to note is that this mixing can also be done in the air. If a bass guitar and a singer are performing a song together, live, then the bass is pushing and pulling the molecules at the same time that the singer’s voice does. So, if at 25 ms, the bass pushes the molecules with a value of 0.5 (whatever that means) and the singer pushes the molecules with a value of 0.1, then your eardrum will be pushed in with a value of 0.6. So, the summation of the pressure signals happens in the air, just like it does as voltages or voltage measurements in the mixing console.

Splitting signals apart

Typically, however, a loudspeaker is comprised of more than one driver – for example, a woofer (for the low frequencies) and a tweeter (for the high frequencies). (Of course, some loudspeakers have more than two drivers, but we’re keeping things simple today…)

So, what we do there is to put the total signal, shown in Figure 5, and send it to two circuits that change how loud things are, depending on their frequency. One circuit is called a “low pass filter” because it allows low frequencies to pass through it unchanged, but it reduces the level of higher frequencies. The other circuit is called a “high pass filter” because it allows the high frequencies to pass through it unchanged, but it reduces the level of the lower frequencies. (we won’t talk about how those circuits do that in this posting…)

We can plot the two characteristics of these two circuits – an example of which is shown in Figure 6.

Figure 6: An example of the gains applied to a signal by a low pass filter (in red) and a high pass filter (in black). Notice that, at one frequency, both filters have the same output level. That frequency is called the “crossover frequency” because it’s the frequency where the two filters’ responses cross over each other.

IF we send a signal like the one in Figure 5 to a crossover that happens to have a crossover frequency that is between the two frequencies it contains, then the signal will be split into two – one output containing mostly low-frequency components, and the other one containing mostly high-frequency components. Examples of these are shown below.

Figure 7: An example of the output of the signal from Figure 5, sent though a low-pass filter. Notice that it looks a lot like Figure 1 (the low frequency component of the combined signal) – but there’s a little bit of Figure 2 (the high frequency component) left in there…

Figure 8: An example of the output of the signal from Figure 5, sent though a high-pass filter. Notice that it looks a lot like Figure 2 (the high frequency component of the combined signal) – but there’s a little bit of Figure 1 (the low frequency component) left in there…

NB: Of course, everything I’ve shown here are just examples to make the concept intuitive. The crossover shown in Figure 6 would not work the way I’ve shown it in Figures 7 and 8 because the crossover frequency is too high compared to the 10 Hz and 50 Hz waves that I used in the example. So, please do not make comments talking about how I chose the wrong crossover frequency…

B&O Tech: Intro to Acoustic Interference and Loudspeaker Directivity

#71 in a series of articles about the technology behind Bang & Olufsen loudspeakers

B&O Tech: The Basics of Sound

#70 in a series of articles about the technology behind Bang & Olufsen loudspeakers

B&O Tech: BeoLab 50 – Set-up procedure

#69 in a series of articles about the technology behind Bang & Olufsen loudspeakers

B&O Tech: BeoLab 50 – Introduction to Features

#68 in a series of articles about the technology behind Bang & Olufsen loudspeakers