Category: loudspeakers

Beosound Theatre: Spatial control

#89 in a series of articles about the technology behind Bang & Olufsen

There are many cases where the number of input channels in the audio signal does not match the number of loudspeakers in your configuration. For example, you may have two loudspeakers, but the input signal is from a multichannel source such as a 7.1-channel stream or a 7.1.4-channel Blu-ray. In this case, the audio must be ‘downmixed’ to your two loudspeakers if you are to hear all components of the audio signal. Conversely, you may have a full surround sound system with 7 main loudspeakers and a subwoofer (a 7.1-channel system) and you would like to re-distribute the two channels from a CD to all of your loudspeakers. In this example, the signal must be ‘upmixed’ to all loudspeakers.

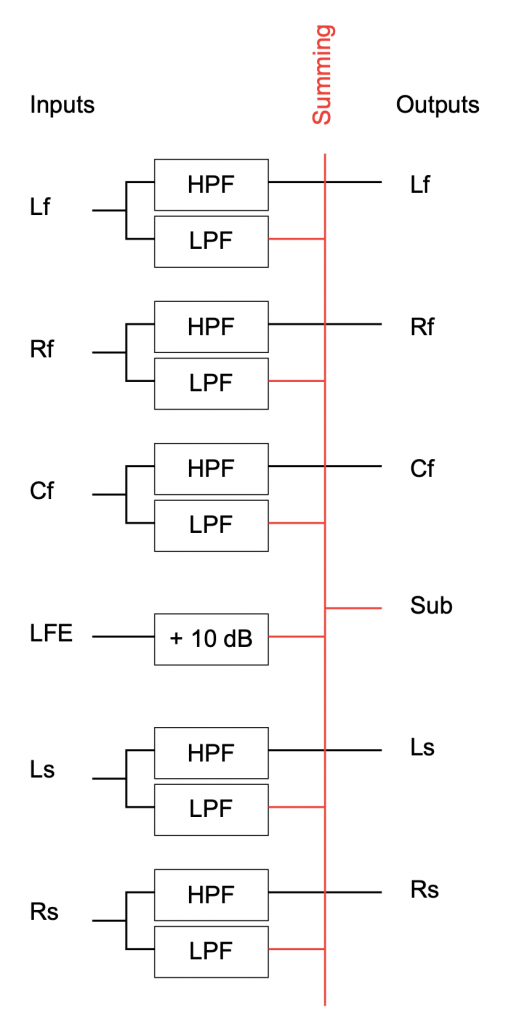
Bang & Olufsen’s True Image is a processor that accomplishes both of these tasks dynamically, downmixing or upmixing any incoming signal so that all components and aspects of the original recording are played using all of your loudspeakers.

Of course, using the True Image processor means that signals in the original recording are re-distributed. For example, in an upmixing situation, portions in the original Left Front signal from the source will be sent to a number of loudspeakers in your system instead of just one left front loudspeaker. If you wish to have a direct connection between input and output channels, then the Processing should be set to ‘Direct’, thus disabling the True Image processing.

Note that, in Direct mode, there may be instances where some input or output channels will not be audible. For example, if you have two loudspeakers but a multichannel input, only two of the input channels will be audible. These channels are dependent on the speaker roles selected for the two loudspeakers. (For example, if your loudspeakers’ roles are Left Front and Right Front, then only the Left Front and Right Front channels from the multichannel source will be heard.)

Similarly, in Direct mode, if you have a multichannel configuration but a two-channel stereo input, then only the loudspeakers assigned to have the Left Front and Right Front speaker roles will produce the sound; all other loudspeakers will be silent.

If True Image is selected and if the number of input channels and their channel assignments matches the speaker roles, and if all Spatial Control sliders are set to the middle position, then the True Image processing is bypassed. For example, if you have a 5.1 loudspeaker system with 5 main loudspeakers (Left Front, Right Front, Centre Front, Left Surround, and Right Surround) and a subwoofer, and the Spatial Control sliders are in the middle positions, then a 5.1 audio signal (from a DVD, for example) will pass through unaffected.

However, if the input is changed to a 2.0 source (i.e. a CD or an Internet radio stream) then the True Image processor will upmix the signal to the 5.1 outputs.

In the case where you wish to have the benefits of downmixing without the spatial expansion provided by upmixing, you can choose to use the Downmix setting in this menu. For example, if you have a 5.1-channel loudspeaker configuration and you wish to downmix 6.1- and 7.1-channel sources (thus ensuring that you are able to hear all input channels) but that two-channel stereo sources are played through only two loudspeakers, then this option should be selected. Note that, in Downmix mode, there are two exceptions where upmixing may be applied to the signal. The first of these is when you have a 2.0-channel loudspeaker configuration and a 1-channel monophonic input. In this case, the centre front signal will be distributed to the Left Front and Right Front loudspeakers. The second case is when you have a 6.1 input and a 7.1 loudspeaker configuration. In this case, the Centre Back signal will be distributed to the Left Back and Right Back loudspeakers.

The Beosound Theatre includes four advanced controls (Surround, Height, Stage Width and Envelopment, described below) that can be used to customise the spatial attributes of the output when the True Image processor is enabled.

Surround

The Surround setting allows you to determine the relative levels of the sound stage (in the front) and the surround information from the True Image processor.

Changes in the Surround setting only have an effect on the signal when the Processing is set to True Image.

Height

This setting determines the level of the signals sent to all loudspeakers in your configuration with a ‘height’ Speaker Role. It will have no effect on other loudspeakers in your system.

If the setting is set to minimum, then no signal will be sent to the ‘height’ loudspeakers.

Changes in the Height setting only have an effect on the signal when the Processing is set to True Image.

Stage Width

The Stage Width setting can be used to determine the width of the front images in the sound stage. At a minimum setting, the images will collapse to the centre of the frontal image. At a maximum setting, images will be pushed to the sides of the front sound stage. This allows you to control the perceived width of the band or music ensemble without affecting the information in the surround and back loudspeakers.

If you have three front loudspeakers (Left Front, Right Front and Centre Front), the setting of the Stage Width can be customised according to your typical listening position. If you normally sit in the ‘sweet spot’, at roughly the same distance from all three loudspeakers, then you should increase the Stage Width setting somewhat, since it is unnecessary to use the centre front loudspeaker to help to pull phantom images towards the centre of the sound stage. The further to either side of the sweet spot that you are seated, the more reducing the Stage Width value will improve the centre image location.

Changes in the Stage Width setting only have an effect on the signal when the Processing is set to True Image.

Envelopment

The Envelopment setting allows you to set the desired amount of perceived width or spaciousness from your surround and back loudspeakers. At its minimum setting, the surround information will appear to collapse to a centre back phantom location. At its maximum setting, the surround information will appear to be very wide.

Changes in this setting have no effect on the front loudspeaker channels and only have an effect on the signal when the Processing is set to True Image.

One last point…

One really important thing to know about the True Image processor is that, if the input signal’s configuration matches the output, AND the 4 sliders described above are in the middle positions, then True Image does nothing. In other words, in this specific case, it’s the same as ‘Direct’ mode.

However, if there is a mis-match between the input and the output channel configuration (for example, 2.0 in and 5.1 out, or 7.1.4 in and 5.1.2 out) then True Image will do something: either upmixing or downmixing. Also, if the input configuration matches the output configuration (e.g. 5.x in and 5.x out) but you’ve adjusted any of the sliders, then True Image will also do something…

Beosound Theatre and Dolby Atmos

#88 in a series of articles about the technology behind Bang & Olufsen

In 2012, Dolby introduced its Dolby Atmos surround sound technology in movie theatres with the release of the Pixar movie, ‘Brave’, and support for the system was first demonstrated on equipment for home theatres in 2014. However, in spite of the fact that it has been 10 years since its introduction, it still helps to offer an introductory explanation to what, exactly, Dolby Atmos is. For more in-depth explanations, https://www.dolby.com/technologies/dolby-atmos is a good place to start and https://www.dolby.com/about/support/guide/speaker-setup-guides has a wide range of options for loudspeaker configuration recommendations.

From the perspective of audio / video systems for the home, Dolby Atmos can most easily be thought of as a collection of different things:

  1. a set of recommendations for loudspeaker configuration that can include loudspeakers located above the listening position
  2. a method of supplying audio signals to those loudspeakers that not only use audio channels that are intended to be played by a single loudspeaker (e.g. Left Front or Right Surround), but also audio objects whose intended spatial positions are set by the mixing engineer, but whose actual spatial position is ‘rendered’ based on the actual loudspeaker configuration in the customer’s listening room.
  3. a method of simulating the spatial positions of ‘virtual’ loudspeakers
  4. the option to use loudspeakers that are intentionally directed away from the listening position, potentially increasing the spatial effects in the mix. These are typically called ‘up-firing’ and ‘side-firing’ loudspeakers.

In addition to this, Dolby has other technologies that have been enhanced to be used in conjunction with Dolby Atmos-encoded signals. Arguably, the most significant of these is an upmixing / downmixing algorithm that can adapt the input signal’s configuration to the output channels.

Note that many online sites state that Dolby’s upmixing / downmixing processor is part of the Dolby Atmos system. This is incorrect. It’s a separate processor.

1. Loudspeaker configurations

Dolby’s Atmos recommendations allow for a large number of different options when choosing the locations of the loudspeakers in your listening room. These range from a simple 2.0.0, traditional two-channel stereo loudspeaker configuration up to a 24.1.10 large-scale loudspeaker array for movie theatres. The figures below show a small sampling of the most common options. (see https://www.dolby.com/about/support/guide/speaker-setup-guides/ for many more possibilities and recommendations.)

Standard loudspeaker configuration for two-channel stereo (Lf / Rf)

Standard loudspeaker configuration for 5.x multichannel audio. The actual angles of the surround loudspeakers at 110 degrees shows the reference placement used at Bang & Olufsen for testing and tuning. Note that the placement of the subwoofer is better determined by your listening room’s acoustics, but it is advisable to begin with a location near the centre front loudspeaker.

Recommended loudspeaker configuration for most 7.x channel audio signals. The actual angles of the loudspeakers shows the reference placement used at Bang & Olufsen for testing and tuning.
Loudspeaker positions associated with the speaker roles available in the Beosound Theatre, showing a full 7.x.4 configuration.

Loudspeaker positions associated with the speaker roles available in the Beosound Theatre, showing a full 7.x.4 configuration.

2. Channels and Objects

Typically, when you listen to audio, regardless of whether it’s monophonic or a stereo (remember that ‘stereo’ merely implies ‘more than one channel’) signal, you are reproducing some number of audio channels that were mixed in a studio. For example, a recording engineer placed a large number of microphones around a symphony orchestra or a jazz ensemble, and then decided on the mix (or relative balance) of those signals that should be sent to a loudspeakers in the left front and right front positions. They did this by listening to the mix through loudspeakers in a standard configuration with the intention that you place your loudspeakers similarly and sit in the correct location.

Consequently, each loudspeaker’s input can be thought of as receiving a ‘pre-packaged’ audio channel of information.

However, in the early 2000s, a new system for delivering audio to listeners was introduced with the advent of powerful gaming consoles. In these systems, it was impossible for the recording engineer to know where a sound should be coming from at any given moment in a game with moving players. So, instead of pre-mixing sound effects (like footsteps, for example) in a fixed position, a monophonic recording of the effect (the footsteps) was stored in the game’s software, and then the spatial position could be set at the moment of playback. So, if the footsteps should appear on the player’s left, then the game console would play them on the left. If the player then turned, the footsteps could be moved to appear in the centre or on the right. In this way different sound objects could be ‘rendered’ instead of merely being reproduced. Of course, the output of these systems was still either loudspeakers or headphones; so the rendered sound objects were mixed with the audio channels (e.g. background music) before being sent to the outputs.

The advantage of a channel-based system is that there is (at least theoretically) a 1:1 match between what the recording or mastering engineer heard in the studio, and what you are able to hear at home. The advantage of an object-based system is that it can not only adapt to the listener’s spatial changes (e.g. the location and rotation of a player inside a game environment) but also to changes in loudspeaker configurations. Change the loudspeakers, and you merely tell the system to render the output differently.

Dolby’s Atmos system merges these two strategies, delivering audio content using both channel-based and object-based streams. By delivering audio channels that match older systems, it becomes possible to have a mix on a newly-released movie that is compatible with older playback systems. However, newer Dolby Atmos-compatible systems can render the object-based content as well, optimising the output for the particular configuration of the loudspeakers.

3. Virtual Loudspeakers

Dolby’s Atmos processing includes the option to simulate loudspeakers in ‘virtual’ locations using ‘real’ loudspeakers placed in known locations. Beosound Theatre uses this Dolby Atmos processing to generate the signals used to create four virtual outputs. (This is discussed in detail in another posting.)

4. Up-firing and Side-firing Loudspeakers

A Dolby Atmos-compatible soundbar or loudspeaker can also include output beams that are aimed away from instead of towards the listening position; either to the sides or above the loudspeakers.

These are commonly known as ‘up-firing’ and ‘side-firing’ loudspeakers. Although Beosound Theatre gives you the option of using a similar concept, it is not merely implemented with a single loudspeaker driver, but with a version of the Beam Width and Beam Direction control used in other high-end Bang & Olufsen loudspeakers. This means that, when using the up-firing and side-firing outputs, more than a single loudspeaker driver is being used to produce the sound. This helps to reduce the beam width, reducing the level of the direct sound at the listening position, which, in turn can help to enhance the spatial effects that can be encoded in a Dolby Atmos mix.

Upmixing and Downmixing

There are cases where an incoming audio signal was intended to be played by a different number of loudspeakers than are available in the playback system. In some cases, the playback uses fewer loudspeakers (e.g. when listening to a two-channel stereo recording on the single loudspeaker on a mobile phone). In other cases, the playback system has more loudspeakers (e.g. when listening to a monophonic news broadcast on a 5.1 surround sound system). When the number of input channels is larger than the number of outputs (typically loudspeakers), the signals have to be downmixed so that you are at least able to hear all the content, albeit at the price of spatially-distorted reproduction. (For example, instruments will appear to be located in incorrect locations, and the spaciousness of a room’s reverberation may be lost.) When the number of output channels (loudspeakers) is larger than the number of input channels, then the system may be used to upmix the signal.

The Dolby processor in a standard playback device has the capability of performing both of these tasks: either upmixing or downmixing when required (according to both the preferences of the listener). One particular feature included in this processing is the option for a mixing engineer to ‘tell’ the playback system exactly how to behave when doing this. For example, when downmixing a 5.1-channel movie to a two-channel output, it may be desirable to increase the level of the centre channel to increase the level of the dialogue to help make it more intelligible. Dolby’s encoding system gives the mixing engineer this option using ‘metadata’; a set of instructions defining the playback system’s behaviour so that it behaves as intended by the artist (the mixing engineer). Consequently, the Beosound Theatre gives you the option of choosing the Downmix mode, where this processing is done exclusively in the Dolby processor.

However, there are also cases where you may also wish to upmix the signal to more loudspeakers than there are input channels from the source material. For these situations, Bang & Olufsen has developed its own up-/down-mixing processor called True Image, which I’ll discuss in more detail in another posting.

Beosound Theatre: A very short history lesson

#87 in a series of articles about the technology behind Bang & Olufsen

Once upon a time, in the incorrectly-named ‘Good Old Days’, audio systems were relatively simple things. There was a single channel of audio picked up by a gramophone needle or transmitted to a radio, and that single channel was reproduced by a single loudspeaker. Then one day, in the 1930s, a man named Alan Blumlein was annoyed by the fact that, when he was watching a film at the cinema and a character moved to one side of the screen, the voice still sounded like it was coming from the centre (because that’s where the loudspeaker was placed). So, he invented a method of simultaneously reproducing more than one channel of audio to give the illusion of spatial changes. (See Patent GB394325A:Improvements in and relating to sound-transmission, sound-recording and sound-reproducing systems’) Eventually, that system was called stereophonic audio.

The word stereo’ first appeared in English usage in the late 1700s, borrowed directly from the French word ‘stéréotype’: a combination of the Greek word στερεó (roughly pronounced ‘stereo’) meaning ‘solid’ and the Latin ‘typus’ meaning ‘form’. ‘Stereotype’ originally meant a letter (the ‘type’) printed (e.g. on paper) using a solid plate (the ‘stereo’). In the mid-1800s, the word was used in ‘stereoscope’ for devices that gave a viewer a three-dimensional visual representation using two photographs. So, by the time Blumlein patented spatial improvements in audio recording and reproduction in the 1930s, the word had already been in used to mean something akin to ‘a three-dimensional representation of something’ for over 80 years.

Over the past 90 years, people have come to mis-understand that ‘stereo’ audio implies only two channels, but this is incorrect, since Blumlein’s patent was also for three loudspeakers, placed on the left, centre, and right of the cinema screen. In fact, a ‘stereo’ system simply means that it uses more than one audio channel to give the impression of sound sources with different locations in space. So it can easily be said that all of the other names that have been used for multichannel audio formats (like ‘quadraphonic’, ‘surround sound’, ‘multichannel audio’, and ‘spatial audio’, just to name a few obvious examples) since 1933 are merely new names for ‘stereo’ (a technique that we call ‘rebranding’ today).

At any rate, most people were introduced to `stereophonic’ audio either through a two-channel LP, cassette tape, CD, or a stereo FM radio receiver. Over the years, systems with more and more audio channels have been developed; some with more commercial success than others. The table below contains a short list of examples.

Some of the information in that list may be surprising, such as the existence of a 7-channel audio system in the 1950s, for example. Another interesting thing to note is the number of multichannel formats that were not `merely’ an accompaniment to a film or video format.

One problem that is highlighted in that list is the confusion that arises with the names of the formats. One good example is ‘Dolby Digital’, which was introduced as a name not only for a surround sound format with 5.1 audio channels, but also the audio encoding method that was required to deliver those channels on optical film. So, by saying ‘Dolby Digital’ in the mid-1990s, it was possible that you meant one (or both) of two different things. Similarly, although SACD and DVD-Audio were formats that were capable of supporting up to 6 channels of audio, there was no requirement and therefore no guarantee that the content be multichannel or that the LFE channel actually contain low-frequency content. This grouping of features under one name still causes confusion when discussing the specifics of a given system, as we’ll discuss below in the section on Dolby Atmos.

FormatIntroducedChannelsNote
Edison phonograph cylinders18961
Berliner gramophone record18971
Wire recorder18981
Optical (on film)ca. 19201
Magnetic Tape19282
Fantasound19403 / 543 channels through 54 loudspeakers
Cinerama1950s7.1Actually 7 channels
Stereophonic LP19572
Compact Cassette19632
Q-8 magnetic tape cartridge19704
CD-4 Quad LP19714
SQ (Stereo Quadraphonic) LP19714
IMAX19715.1
Dolby Stereo19754aka Dolby Surround
Compact Disc19832
DAT19872
Mini-disc19922
Digital Compact Cassette19922
Dolby Digital19925.1
DTS Coherent Acoustics19935.1
Sony SDDS19997.1
SACD19995.1Actually 6 full-band channels
Dolby EX19996.1
Tom Holman / TMH Labs199910.2
DVD-Audio20005.1Actually 6 full-band channels
DTS ES20006.1
NHK Ultra-high definition TV200522.2
Auro 3D20059.1 to 26.1
Dolby Atmos2012up to 24.1.10

Looking at the column listing the number of audio channels in the different formats, you may have three questions:

  • Why does it say only 4 channels for Dolby Stereo? I saw Star Wars in the cinema, and I remember a LOT more loudspeakers on the walls.
  • What does the `.1′ mean? How can you have one-tenth of an audio channel?
  • Some of the channel listings have one or two numbers and some have three, which I’ve never seen before. What do the different numbers represent?

Input Channels and Speaker Roles

A ‘perfect’ two-channel stereo system is built around two matched loudspeakers, one on the left and the other on the right, each playing its own dedicated audio channel. However, when better sound systems were developed for movie theatres, the engineers (starting with Blumlein) knew that it was necessary to have more than two loudspeakers because not everyone is sitting in the middle of the theatre. Consequently, a centre loudspeaker was necessary to give off-centre listeners the impression of speech originating in the middle of the screen. In addition, loudspeakers on the side and rear walls helped to give the impression of envelopment for effects such as rain or crowd noises.

It is recommended but certainly not required, that a given Speaker Role should only be directed to one loudspeaker. In a commercial cinema, for example, a single surround channel is most often produced by many loudspeakers arranged on the side and rear walls. This can also be done in larger home installations where appropriate.

Similarly, in cases where the Beosound Theatre is accompanied by two larger front loudspeakers, it may be preferable to use the three front-firing outputs to all produce the Centre Front channel (instead of using the centre output only).

x.1 ?

The engineers also realised that it was not necessary that all the loudspeakers be big, and therefore requiring powerful amplifiers. This is because larger loudspeakers are only required for high-level content at low frequencies, and we humans are terrible at locating low-frequency sources when we are indoors. This meant that effects such as explosions and thunder that were loud, but limited to the low-frequency bands could be handled by a single large unit instead; one that handled all the content below the lowest frequencies capable of being produced by the other loudspeakers’ woofers. So, the systems were designed to rely on a powerful sub-woofer that driven by a special, dedicated Low Frequency Effects (or LFE) audio channel whose signals were limited up to about 120 Hz. However, as is discussed in the section on Bass Management, it should not be assumed that the LFE input channel is only sent to a subwoofer; nor that the only signal produced by the subwoofer is the LFE channel. This is one of the reasons it’s important to keep in mind that the LFE input channel and the subwoofer output channel are separate concepts.

Since the LFE channel only contains low frequency content, it has only a small fraction of the bandwidth of the main channels. (‘Bandwidth’ is the total frequency width of the signal. In the case of the LFE channel it is up to about 120 Hz. (In fact, different formats have different bandwidths for the LFE channel, but 120 Hz is a good guess.) In the case of a main channel, it is up to about 20,000 Hz; however these values are not only fuzzy but dependent on the specifications of distribution format, for example.) Although that fraction is approximately 120/20000, we generously round it up to 1/10 and therefore say that, relative to a main audio channel like the Left Front, the LFE signal is only 0.1 of a channel. Consequently, you’ll see audio formats with something like ‘5.1 channels’ meaning `5 main channels and an LFE channel’. (This is similar to the way rental apartments are listed in Montr\’eal, where it’s common to see a description such as a 3 1/2; meaning that it has a living room, kitchen, bedroom, and a bathroom (which is obviously half of a room).)

LFE ≠ Subwoofer

Many persons jump to the conclusion that an audio input with an LFE channel (for example, a 5.1 or a 7.1.4 signal) means that there is a ‘subwoofer’ channel; or that a loudspeaker configuration with 5 main loudspeakers and a subwoofer is a 5.1 configuration. It’s easy to make this error because those are good descriptions of the way many systems have worked in the past.

However, systems that use bass management break this direct connection between the LFE input and the subwoofer output. For example, if you have two large loudspeakers such as Beolab 50s or Beolab 90s for your Lf / Rf pair, it may not be necessary to add a subwoofer to play signals with an LFE channel. In fact, in these extreme cases, adding a subwoofer could result in downgrading the system. Similarly, it’s possible to play 2.0-channel signal through a system with two smaller loudspeakers and a single subwoofer.

Therefore, it’s important to remember that the ‘x.1’ classification and the discussion of an ‘LFE’ channel are descriptions of the input signal. The output may or may not have one or more subwoofers; and these two things are essentially made independent of each other using a bass management system.

x.y.4 ?

If you look at the table above, you’ll see that some formats have very large numbers of channels, however, these numbers can be easily mis-interpreted. For example, in both the ‘10.2’ and ‘22.2’ systems, some of the audio channels are intended to be played through loudspeakers above the listeners, but there’s no way to know this simply by looking at the number of channels. This is why we currently use a new-and-improved method of listing audio channels with three numbers instead of two.

  • The first number tells you how many ‘main’ audio channels there are. In an optimal configuration, these should be reproduced using loudspeakers at the listeners’ ear heights.
  • The second number tells you how many LFE channels there are.
  • The third number tells you how many audio channels are intended to be reproduced by loudspeakers located above the listeners.

For example, you’ll notice looking at the table below, that a 7.1.4 channel system contains seven main channels around the listeners, one LFE channel, and four height channels.

Speaker Role2.05.17.17.1.4
Left Frontxxxx
Right Frontxxxx
Centre Frontxxx
LFExxx
Left Surroundxxx
Right Surroundxxx
Left Backxx
Right Backxx
Left Front Heightx
Right Front Heightx
Left Surround Heightx
Right Surround Heightx

It is worth noting here that the logic behind the Bang & Olufsen naming system is either to avoid having duplicate letters for different role assignments, or to reserve options for future formats. For example, ‘Back’ is used instead of ‘Rear’ to prevent confusion with ‘Right, and ‘Height’ is used instead of ‘Top’ because another, higher layer of loudspeakers may be used in future formats. (The ‘Ceiling’ loudspeaker channel used in multichannel recordings from Telarc is an example of this.)

Bass Management in Beosound Theatre

#84 in a series of articles about the technology behind Bang & Olufsen loudspeakers

In a perfect sound system, all loudspeakers are identical, and they are all able to play a full frequency range at any listening level. However, most often, this is not a feasible option, either due to space or cost considerations (or both…). Luckily, it is possible to play some tricks to avoid having to install a large-scale sound system to listen to music or watch movies.

Humans have an amazing ability to localise sound sources. With your eyes closed, you are able to point towards the direction sounds are coming from with an incredible accuracy. However, this ability gets increasingly worse as we go lower in frequency, particularly in closed rooms.

In a sound system, we can use this inability to our advantage. Since you are unable to localise the point of origin of very low frequencies indoors, it should not matter where the loudspeaker that’s producing them is positioned in your listening room. Consequently, many simple systems remove the bass from the “main” loudspeakers and send them to a single large loudspeaker whose role it is to reproduce the bass for the entire system. This loudspeaker is called a “subwoofer”, since it is used to produce frequency bands below those played by the woofers in the main loudspeakers.

The process of removing the bass from the main channels and re-routing them to a subwoofer is called bass management.

It’s important to remember that, although many bass management systems assume the presence of at least one subwoofer, that output should not be confused with an (Low-Frequency Effects) LFE (Low-Frequency Effects) or a “.1” input channel. However, in most cases, the LFE channel from your media (for example, a Blu-ray disc or video streaming device) will be combined with the low-frequency output of the bass management system and the total result routed to the subwoofer. A simple example of this for a 5.1-channel system is shown below in Figure 1.

Figure 1: A simple example of a bass management system for a 5.1 channel system.

Of course, there are many other ways to do this. One simplification that’s usually used is to put a single Low Pass Filter (LPF) on the output of the summing buss after the signals are added together. That way, you only need to have the processing for one LPF instead of 5 or 6. On the other hand, you might not want to apply a LPF to an LFE input, so you may want to add the main channels, apply the LPF, and then add the LFE, for example. Other systems such as Bang & Olufsen televisions use a 2-channel bass management system so that you can have two subwoofers (or two larger main loudspeakers) and still maintain left/right differences in the low frequency content all the way out to the loudspeakers.

However, the one thing that older bass management systems have in common is that they typically route the low frequency content to a subset of the total number of loudspeakers. For example, a single subwoofer, or the two main front loudspeakers in a larger multichannel system.

In Bang & Olufsen televisions starting with the Beoplay V1 and going through to the Beovision Harmony, it is possible to change this behaviour in the setup menus, and to use the “Re-direction Level” to route the low frequency output to any of the loudspeakers in the current Speaker Group. So, for example, you could choose to send the bass to all loudspeakers instead of just one subwoofer.

There are advantages and disadvantages to doing this.

The first advantage is that, by sending the low frequency content to all loudspeakers, they all work together as a single “subwoofer”, and thus you might be able to get more total output from your entire system.

The second advantage is that, since the loudspeakers are (probably) placed in different locations around your listening room, then they can work together to better control the room’s resonances (a.k.a. room modes).

One possible disadvantage is that, if you have different loudspeakers in your system (say, for example, Beolab 3s, which have slave drivers, and Beolab 17s, which use a sealed cabinet design) then your loudspeakers may have different frequency-dependent phase responses. This can mean in some situations that, by sending the same signal to more loudspeakers, you get a lower total acoustic output in the room because the loudspeakers will cancel each other rather than adding together.

Another disadvantage is that different loudspeakers have different maximum output levels. So, although they may all have the same output level at a lower listening level, as you turn the volume up, that balance will change depending on the signal level (which is also dependent on frequency content). For example, if you own Beolab 17s (which are small-ish) and Beolab 50s (which are not) and if you’re listening to a battle scene with lots of explosions, at lower volume levels, the 17s can play as much bass as the 50s, but as you turn up the volume, the 17s reach their maximum limit and start protecting themselves long before the 50s do – so the balance of bass in the room changes.

Beosound Theatre

Beosound Theatre uses a new Bass Management system that is an optimised version of the one described above, with safeguards built-in to address the disadvantages. To start, the two low-frequency output channels from the bass management system are distributed to all loudspeakers in the system that are currently being used.

However, in order to ensure that the loudspeakers don’t cancel each other, the Beosound Theatre has Phase Compensation filters that are applied to each individual output channel (up to a maximum of 7 internal outputs and 16 external loudspeakers) to ensure that they work together instead against each other when reproducing the bass content. This is possible because we have measured the frequency-dependent phase responses of all B&O loudspeakers going as far back in time as the Beolab Penta, and created a custom filter for each model. The appropriate filters are chosen and applied to each individual outputs accordingly.

Secondly, we also know the maximum bass capability of each loudspeaker. Consequently, when you choose the loudspeakers in the setup menus of the Beosound Theatre, the appropriate Bass Management Re-direction levels are calculated to ensure that, for bass-heavy signals at high listening levels, all loudspeakers reach their maximum possible output simultaneously. This means that the overall balance of the entire system, both spatially and timbrally, does not change.

The total result is that, when you have external loudspeakers connected to the Beosound Theatre, you are ensured the maximum possible performance from your system, not only in terms of total output level, but also temporal control of your listening room.

Filters and Ringing: Part 10

There’s one last thing that I alluded to in a previous part of this series that now needs discussing before I wrap up the topic. Up to now, we’ve looked at how a filter behaves, both in time and magnitude vs. frequency. What we haven’t really dealt with is the question “why are you using a filter in the first place?”

Originally, equalisers were called that because they were used to equalise the high frequency levels that were lost on long-distance telephone transmissions. The kilometres of wire acted as a low-pass filter, and so a circuit had to be used to make the levels of the frequency bands equal again.

Nowadays we use filters and equalisers for all sorts of things – you can use them to add bass or treble because you like it. A loudspeaker developer can use them to correct linear response problems caused by the construction or visual design of the device. They can be used to compensate for the acoustical behaviour of a listening room. Or they can be used to compensate for things like hearing loss. These are just a few examples, but you’ll notice that three of the four of them are used as compensation – just like the original telephone equalisers.

Let’s focus on this application. You have an issue, and you want to fix it with a filter.

IF the problem that you’re trying to fix has a minimum phase characteristic, then a minimum phase filter (implemented either as an analogue circuit or in a DSP) can be used to “fix” the problem not only in the frequency domain – but also in the time domain. IF, however, you use a linear phase filter to fix a minimum phase problem, you might be able to take care of things on a magnitude vs. frequency analysis, but you will NOT fix the problem in the time domain.

This is why you need to know the time-domain behaviour of the problem to choose the correct filter to fix it.

For example, if you’re building a room compensation algorithm, you probably start by doing a measurement of the loudspeaker in a “reference” room / location / environment. This is your target.

You then take the loudspeaker to a different room and measure it again, and you can see the difference between the two.

In order to “undo” this difference with a filter (assuming that this is possible) one strategy is to start by analysing the difference in the two measurements by decomposing it into minimum phase and non-minimum phase components. You can then choose different filters for different tasks. A minimum phase filter can be used to compensate a resonance at a single frequency caused by a room mode. However, the cancellation at a frequency caused by a reflection is not minimum phase, so you can’t just use a filter to boost at that frequency. An octave-smoothed or 1/3-octave smoothed measurement done with pink noise might look like you fixed the problem – but you’ve probably screwed up the time domain.

Another, less intuitive example is when you’re building a loudspeaker, and you want to use a filter to fix a resonance that you can hear. It’s quite possible that the resonance (ringing in the time domain) is actually associated with a dip in the magnitude response (as we saw earlier). This means that, although intuition says “I can hear the resonant frequency sticking out, so I’ll put a dip there with a filter” – in order to correct it properly, you might need to boost it instead. The reason you can hear it is that it’s ringing in the time domain – not because it’s louder. So, a dip makes the problem less audible, but actually worse. In this case, you’re actually just attenuating the symptom, not fixing the problem – like taking an Asprin because you have a broken leg. Your leg is still broken, you just can’t feel it.

“High-Res” Audio: Part 12: Outputs

Part 1
Part 2
Part 3
Part 4
Part 5
Part 6
Part 7
Part 8a
Part 8b
Part 9
Part 10
Part 11

This series has flipped back and forth between talking about high resolution audio files & sources and the processing that happens in the equipment when you play it. For this posting, we’re going to deal exclusively with the playback side – regardless of the source content.

I work for a company that makes loudspeakers (among other things). All of the loudspeakers we make use digital signal processing instead of resistors, capacitors, and inductors because that’s the best way to do things these days…

Point 1: This means that our volume control is a gain (a multiplier) that’s applied to the digital signal.

We also make surround processors (most of our customers call them “televisions”) that take a multichannel audio input (these days, this is under the flag of “spatial audio”, but that’s just a new name on an old idea) and distribute the signals to multiple loudspeakers. Consequently, all of our loudspeakers have the same “sensitivity”. This is a measurement of how loud the output is for a given input.

Let’s take one loudspeaker model, Beolab 90, as an example. The sensitivity of this loudspeaker is set to be the same as all other Bang & Olufsen loudspeakers. Originally, this was based on an analogue signal, but has since been converted to digital.

Point 2: Specifically, if you send a 0 dB FS signal into a Beolab 90 set to maximum volume, then it will produce a little over 122 dB SPL at 1 m in a free field (theoretically).

Let’s combine points 1 and 2, with a consideration of bit depth on the audio signal.

If you have a DSP-based loudspeaker with a maximum output of 122 dB SPL, and you play a 16-bit audio signal with nothing but TPDF dither, then the noise floor caused by that dither will be 122 – 93 = 29 dB SPL which is pretty loud. Certainly loud enough for a customer to complain about the noise coming from their loudspeaker.

Now, you might say “but no one would play a CD at maximum volume on that loudspeaker” to which I say two things:

  1. I do.
    The “Banditen Galop” track from Telarc’s disc called “Ein Straussfest” has enough dynamic range that this is not dangerous. You just get very loud, but very short spikes when the gunshots happen.
  2. That’s not the point I’m trying to make anyway…

The point I’m trying to make is that, if Beolab 90 (or any other Bang & Olufsen loudspeaker) used 16-bit DACs, then the noise floor would be 29 dB SPL, regardless of the input signal’s bit depth or dynamic range.

So, the only way to ensure that the DAC (or the bit depth of the signal feeding the DAC) isn’t the source of the noise floor from the loudspeaker is to use more than 16 bits at that point in the signal flow. So, we use a 24-bit DAC, which gives us a (theoretical) noise floor of 122 – 141 = -19 dB SPL. Of course, this is just a theoretical number, since there are no DACs with a 141 dB dynamic range (not without doing some very creative cheating, but this wouldn’t be worth it, since we don’t really need 141 dB of dynamic range anyway).

So, there are many cases where a 24-bit DAC is a REALLY good idea, even though you’re only playing 16-bit recordings.

Similarly, you want the processing itself to be running at a higher resolution than your DAC, so that you can control its (the DAC’s) signal (for example, you want to create the dither in the DSP – not hope that the DAC does it for you. This is why you’ll often see digital signal processing running at floating point (typically 32-bit floating point) or fixed point with a wider bit depth than the DAC.

“High-Res” Audio: Part 5 – Mirrors are bad

Part 1
Part 2
Part 3
Part 4

Let’s go back to something I said in the last post:

Mistake #1

I just jumped to at least three conclusions (probably more) that are going to haunt me.

The first was that my “digital audio system” was something like the following:

Figure 1

As you can see there, I took an analogue audio signal, converted it to digital, and then converted it back to analogue. Maybe I transmitted it or stored it in the part that says “digital audio”.

However, the important, and very probably incorrect assumption here is that I did nothing to the signal. No volume control, no bass and treble adjustments… nothing.

If you consider that signal flow from the position of an end-consumer playing a digital recording, this was pretty easy to accomplish in the “old days” when we were all playing CDs. That’s because (in a theoretical, oversimplified world…)

  • the output of the mixing/mastering console was analogue
  • that analogue signal was converted to digital in the mastering studio
  • the resulting bits were put on a disc
  • you put that disc in your player which contained a DAC that converted the signal directly to analogue
  • you then sent the signal to your “processing” (a.k.a. “volume control”, and maybe some bass and treble adjustment.).

So, that flowchart in Figure 1 was quite often true in 1985.

These days, things are probably VERY different… These days, the signal path probably looks something more like this (note that I’ve highlighted “alterations” or changes in the bits in the audio signal in red):

  • The signal was converted from analogue to digital in the studio
    (yes, I know… studios often work with digital mixers these days, but at least some of the signals within the mix were analogue to start – unless you are listening to music made exclusively with digital synthesizers)
  • The resulting bits were saved on a file
  • Depending on the record label, the audio signal was modified to include a “watermark” that can identify it later – in court, when you’ve been accused of theft.
  • The file was transferred to a storage device (let’s say “hard drive”) in a large server farm renting out space to your streaming service
  • The streaming service encodes the file
    • If the streaming service does not offer an lossless option, then the file is converted to a lossy format like MP3, Ogg Vorbis, AAC, or something else.
    • If the streaming service offers a lossless option, then the file is compressed using a format like FLAC or ALAC (This is not an alteration, since, with a lossless compression system, you don’t lose anything)
  • You download the file to your computer
    (it might look like an audio player – but that means it’s just a computer that you can’t use to check your social media profile)
  • You press play, and the signal is decoded (either from the lossy CODEC or the compression format) back to LPCM. (Still not an alteration. If it’s a lossy CODEC, then the alteration has already happened.)
  • That LPCM signal might be sample-rate converted
  • The streaming service’s player might do some processing like dynamic range compression or gain changes if you’ve asked it to make all the songs have the same level.
  • All of the user-controlled “processing” like volume controls, bass, and treble, are done to the digital signal.
  • The signal is sent to the loudspeaker or headphones
    • If you’re sending the signal wirelessly to a loudspeaker or headphones, then the signal is probably re-encoded as a lossy CODEC like AAC, aptX, or SBC.
      (Yes, there are exceptions with wireless loudspeakers, but they are exceptions.)
    • If you’re sending the signal as a digital signal over a wire (like S/PDIF or USB), the you get a bit-for-bit copy at the input of the loudspeaker or headphones.
  • The loudspeakers or headphones might sample-rate convert the signal
  • The sound is (finally) converted to analogue – either one stream per channel (e.g. “left”) or one stream per loudspeaker driver (e.g. “tweeter”) depending on the product.

So, as you can see in that rather long and complicated list (it looks complicated, but I’ve actually simplified it a little, believe it or not), there’s not much relation to the system you had in 1985.

Let’s take just one of those blocks and see what happens if things go horribly wrong. I’ll take the “volume control” block and add some distortion to see the result with two LPCM systems that have two different sampling rates, one running at 48 kHz and the other at 194 kHz – four times the rate. Both systems are running at 24 bits, with TPDF dither (I won’t explain what that means here). I’ll start by making a 10 kHz tone, and sending it through the system without any intentional distortion. If we look at those two signals in the time domain, they’ll look like this:

Figure 1: Two 10 kHz tones. The black one is in a 48 kHz, 24 bit LPCM system. The red one is in a 192 kHz, 24 bit LPCM system.

The sine tone in the 48 kHz system may look less like a sine tone than the one in the 192 kHz system, however, in this case, appearances are deceiving. The reconstruction filter in the DAC will filter out all the high frequencies that are necessary to reproduce those corners that you see here, so the resulting output will be a sine wave. Trust me.

If we look at the magnitude responses of these two signals, they look like Figure 2, below.

Figure 2: The magnitude responses of the two signals shown in Figure 1.

You may be wondering about the “skirts” on either side of the 10 kHz spikes. These are not really in the signal, they’re a side-effect (ha ha) of the windowing process used in the DFT (aka FFT). I will not explain this here – but I did a long series of articles on windowing effects with DFTs, so you can search for it if you’re interested in learning more about this.

If you’re attentive, you’ll notice that both plots extend up to 96 kHz. That’s because the 192 kHz system on the bottom has a Nyquist frequency of 96 kHz, and I want both plots to be on the same scale for reasons that will be obvious soon.

Now I want to make some distortion. In order to make things obvious, I’m going to make a LOT of distortion. I’ve made the sine wave try to have an amplitude that is 10 times higher than my two systems will allow. In other words, my amplitude should be +/- 10, but the signal clips at +/- 1, resulting in something looking very much like a square wave, as shown in Figure 3.

Figure 3: Distorted 10 kHz sine waves. The black one is in a 48 kHz, 24 bit LPCM system. The red one is in a 192 kHz, 24 bit LPCM system.

You may already know that if you want to make a square wave by building it up using its constituent harmonics, you need to have the fundamental (which we’ll call Fc. In our case, Fc = 10 kHz) with an amplitude that we’ll say is “A”, you then add the

  • 3rd harmonic (3 times Fc, so 30 kHz in our case) with an amplitude of A/3.
  • 5th harmonic (5 Fc = 50 kHz) with an amplitude of A/5
  • 7 Fc at A/7
  • and so on up to infinity

Let’s look at the magnitude responses of the two signals above to see if that’s true.

Figure 4: The magnitude responses of the two signals shown in Figure 3.

If we look at the bottom plot first (running at 192 kHz and with a Nyquist limit of 96 kHz) the 10 kHz tone is still there. We can also see the harmonics at 30 kHz, 50 kHz, 70 kHz, and 90 kHz in amongst the mess of other spikes we’ll get to those soon…)

Figure 5. Some labels applied to Figure 4 for clarity, showing the harmonics of the square waves that are captured by the two systems

Looking at the top plot (running at 48 kHz and with a Nyquist limit of 24 kHz), we see the 10 kHz tone, but the 30 kHz harmonic is not there – because it can’t be. Signals can’t exist in our system above the Nyquist limit. So, what happens? Think back to the images of the rotating wheel in Part 3. When the wheel was turning more than 1/2 a turn per frame of the movie, it appears to be going backwards at a different speed that can be calculated by subtracting the actual rotation from 180º (half-a-turn).

The same is true when, inside a digital audio signal flow, we try to make a signal that’s higher than Nyquist. The energy exists in there – it just “folds” to another frequency – its “alias”.

We can look at this generally using Figure 6.

Figure 6: A general plot of aliasing, showing the intended frequency in black and the actual output frequency in red.

Looking at Figure 6: If we make a sine tone that sweeps upward from 0 Hz to the Nyquist frequency at Fs/2 (half the sampling rate or sampling frequency) then the output is the same as the input. However, when the intended frequency goes above Fs/2, the actual frequency that comes out is Fs/2 minus the intended frequency. This creates a “mirror” effect.

If the intended frequency keeps going up above Fs, then the mirroring happens again, and again, and again… This is illustrated in Figure 7.

Figure 7: An extension of Figure 5 to a higher intended frequency.

This plot is shown with linear scales for both the X- and Y-axes to make it easy to understand. If the axes in Figure 7 were scaled to a logarithmic scaling instead (which is how “Frequency Response” are normally shown, since this corresponds to how we hear frequency differences), then it would look like Figure 8.

Figure 8: The same information shown in Figure 7, plotted on a logarithmic scale instead. Note that this example is for a system running at 48 kHz (therefore with a Nyquist frequency of 24 kHz), and an intended input frequency (in black) going up to 3 times 48 kHz = 144 kHz.

Coming back to our missing 30 kHz harmonic in the 48 kHz LPCM system: Since 30 kHz is above the Nyquist limit of 24 kHz in that system, it mirrors down to 24 kHz – (30 kHz – 24 kHz) = 18 kHz. The 50 kHz harmonic shows up as an alias at 2 kHz. (follow the red line in Figure 7: A harmonic on the black line at 48 kHz would actually be at 0 Hz on the red line. Then, going 2000 Hz up to 50 kHz would bring the red line up to 2 kHz.)

Similarly, the 110 kHz harmonic in the 192 kHz system will produce an alias at 96 kHz – (110 kHz – 96 kHz) = 82 kHz.

If I then label the first set of aliases in the two systems, we get Figure 9.

Figure 9: The first set of aliased frequency content in the two systems.

Now we have to stop for a while and think about what’s happened.

We had a digital signal that was originally “valid” – meaning that it did not contain any information above the Nyquist frequency, so nothing was aliasing. We then did something to the signal that distorted it inside the digital audio path. This produced harmonics in both cases, however, some of the harmonics that were produced are harmonically related to the original signal (just as they ought to be) and others are not (because they’re aliases of frequency content that cannot be reproduced by the system.

What we have to remember is that, once this happens, that frequency content is all there, in the signal, below the Nyquist frequency. This means that, when we finally send the signal out of the DAC, the low-pass filtering performed by the reconstruction filter will not take care of this. It’s all part of the signal.

So, the question is: which of these two systems will “sound better” (whatever that means)? (I know, I know, I’m asking “which of these two distortions would you prefer?” which is a bit of a weird question…)

This can be answered in two ways that are inter-related.

The first is to ask “how much of the artefact that we’ve generated is harmonically related to the signal (the original sine tone)?” As we can see in Figure 5, the higher the sampling rate, the more artefacts (harmonics) will be preserved at their original intended frequencies. There’s no question that harmonics that are harmonically related to the fundamental will sound “better” than tones that appear to have no frequency relationship to the fundamental. (If I were using a siren instead of a constant sine tone, then aliased harmonics are equally likely to be going down or up when the fundamental frequency goes up… This sounds weird.)

The second is to look at the levels of the enharmonic artefacts (the ones that are not harmonically related to the fundamental). For example, both the 48 kHz and the 192 kHz system have an aliased artefact at 2 kHz, however, its level in the 48 kHz system is 15 dB below the fundamental whereas, in the 192 kHz system, it’s more than 26 dB below. This is because the 6 kHz artefact in the 48 kHz system is an alias of the 30 kHz harmonic, whereas, in the 192 kHz system, it’s an alias of the 190 kHz harmonic, which is much lower in level.

As I said, these two points are inter-related (you might even consider them to be the same point) however, they can be generalised as follows:

The higher the sampling rate, the more the artefacts caused by distortion generated within the system are harmonically related to the signal.

In other words, it gives a manufacturer more “space” to screw things up before they sound bad. The title of this posting is “Mirrors are bad” but maybe it should be “Mirrors are better when they’re further away” instead.

Of course, the distortion that’s actually generated by processing inside a digital audio system (hopefully) won’t be anything like the clipping that I did to the signal. On the other hand, I’ve measured some systems that exhibit exactly this kind of behaviour. I talked about this in another series about Typical Problems in Digital Audio: Aliasing where I showed this measurement of a real device:

Figure 10: A measurement of a real device showing some kind of distortion and aliased artefacts of a swept sine tone. Half of the aliasing is immediately recognizable as going downwards when the tone is going upwards.

However, I’m not here to talk about what you can or can’t hear – that is dependent on too many variables to make it worth even starting to talk about. The point of this series is not to prove that something is better or worse than something else. It’s only to show the advantages and disadvantages of the options so that you can make an informed choice that best suits your requirements.

On to Part 6

What Use are Watts?

#83 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Imagine water coming out of a garden hose, filling up a watering can (it’s nice outside, so this is the first analogy that comes to mind…). The water is pushed out of the hose by the pressure of the water behind it. The higher the pressure, the more water will come out, and the faster the watering can will fill.

If you want to reduce the amount of water coming out of the hose, you can squeeze it, restricting the flow by making a resistance that reduces the water pressure. The higher the resistance of the restriction to the flow, the less water comes out, and the slower the watering can fills up.

Electricity works in a similar fashion. There is an electrical equivalent of the “pressure”, which is called Electromotive Force or EMV, measured in Volts (which is why most people call it “Voltage” instead of its real name). The “flow” – the quantity of electrons that are flowing through the wire – is the current, measured in Amperes or Amps. A thing that restricts the flow of the electrons is called a resistor, since it resists the current. A resistor can be a thing that does nothing except restrict the current for some reason. It could also be something useful. A toaster, for example, is just a resistor as far as the power company is concerned. So is a computer, your house, or an entire city.

So, if we measure the current coming through a wire, and we want to increase it, we can increase the voltage (the electrical pressure) or we can reduce the resistance. These three are locked together. For example, if you know the voltage and the resistance, you can calculate the current. Or, if you know the current and the resistance, you can calculate the voltage. This is done with a very simple equation known as Ohm’s law:

V = I*R

Where V is the Voltage in Volts, I is the current in Amperes, and R is the resistance in Ohms.

For example, if you have a toaster plugged into a wall socket that is delivering 230 V, and you measure 2 Amperes of current going through it, then :

R = V / I

R = 230 / 4

R = 57.5 Ohms

However, to be honest, I don’t really care what the resistance of my toaster is. What concerns me most is how much I have to pay the power company every time I make toast. How is this calculated? Well, the power company promises to always give me 230 V at my disposal in the wall socket. The amount of current that I use is up to me. If I plug in a big resistance (like an LED lamp) then I don’t use much current. If I plug in a small resistance (say, to charge up the battery in the electric car) then I use lots. What they’re NOT doing is charging me for the current – although it does enter into another equation. The power company is charging me for the amount of Power that I’m using – because they’re charging me for the amount of work that they have to do to generate it for me.

When I use a toaster, it’s converting electrical energy into heat. The amount of heat that it generates is dependent on the voltage (the electrical pressure) and the current going through it. This can be calculated using another simple equation knowns as “Watt’s Law”:

P = V * I

So, let’s say that I plug my toaster into a 230 V outlet, and, because it is a 115 Ohm resistor, 2 Amperes goes through it. In this case, then the amount of Power it’s consuming is

P = 230 * 4

P = 920 Watts

If I’m going to be a little specific, then I should say that the Power (in Watts) is a measure of how much energy I’m transferring per second – so there’s an aspect of time here that I’m ignoring, but this won’t be important until the end of this posting.

Also, if I’m going to bring this back to the power company’s bill that they send me at the end of the month, it will be not only based on how much power I used (in Watts), but how long I used it for (in hours). So, if I make toast for 1 minute, then I used 920 Watts for 1/60th of an hour, therefore I have to pay for

920 / 60 = 15.33 Watt hours

Normally, of course, I do more than make toast once a month. In fact, I use a LOT more, so it’s measured in thousands of Watt hours or “kilowatt hours”.

For example, if I pull into the driveway with an almost-flat battery in our car, and I plug it into the special outlet we have for charging it to charge, I know that it’s using about 26 Amperes and the outlet is fixed at 380 V. This means that I’m using 10,000 Watts, and it will therefore take about 6.4 hours to charge the car (because it has a 64,000 Wh or 64 kWh battery). This means, at the end of the month, I’ll have to pay for those 64 kWh that I used to charge up the car.

So what? (So watt?)

When you play music in a loudspeaker driver, the amplifier “sees” the driver as a resistor.* Let’s say, for the purposes of this discussion, that the driver has a resistance of 8 Ohms. (It doesn’t, but today, we’ll pretend.) To play the music, the amplifier sends a signal that, on an oscilloscope, looks like the signal that came out of a microphone once-upon-a-time (yes – I’m oversimplifying). That signal that you’re looking at is the VOLTAGE that the amplifier is creating to make the signal. Since the loudspeaker driver has some resistance, we can therefore calculate the current that it “asks” the amplifier to deliver. As the voltage goes up, the current goes up, because the resistance stays the same (yes – I’m oversimplifying).

Now, let’s think about this: The amplifier is generating a voltage, and therefore it has to deliver a current. If I multiply those two things together, I can get the power: P = V*I. Simple, right?

Well, yes…. but remember that thing I said above about how power, in Watts, has an element of time. One watt is a measure of energy that is transferred into a thing (in our case, a loudspeaker driver) in one second. And this is where things get complicated, and increasingly irrelevant.

The problem is that power, measured in watts, has an underlying assumption that the consumption is constant. Turn on an old-fashioned light bulb or start making toast, and the power that you consume over time will be the same. However, when you’re playing Stravinsky on a loudspeaker, the voltage and the current are going up and down all the time – if they weren’t, you’d be listening to a sine wave, which is boring.

So, although it’s easy to use Watts to specify a the amount of energy an amplifier can deliver or a loudspeaker driver’s capabilities, it’s not really terribly useful. Instead, it’s much more useful to know how many volts the amplifier can deliver, and how many amperes it can push out before it can’t deliver more (and therefore distorts). However, although you know the maximum voltage and the maximum current, this is not necessarily the maximum power, since it might only be able to deliver those maxima for a VERY short period of time.

For example, if you measure the peak voltage and the peak current that comes out of all of the amplifiers in a Beolab 90 for less than 5 thousandths of a second (5 milliseconds), the you’ll get to a crazy number like 18,000 Watts. However, after about 5 ms, that number drops very rapidly. It can deliver the peak, but it can’t deliver it continuously (if it could, you’d trip a circuit breaker). (Similarly, you can drive a nail into wood by hitting it with a hammer – but you can’t push it in like a thumbtack. The amount of force you can deliver in a short peak is much higher than the amount you can deliver continuously.)

This is why, when we are specifying a power amplifier that we’ll need for a new loudspeaker at the beginning of the development process, we specify it in Peak Voltage and Peak Current (also the continuous values as well, of course) – but not Watts. Yes, you can use one to calculate the other, but consider this:

Amplifier #1: 1000 W amplifier, capable of delivering 10 V and 100 Amps

Amplifier #2: 1000 W amplifier, capable of delivering 100 V and 10 Amps

These are two VERY different things – so just saying a “1000 W amplifier” is not nearly enough information to be useful to anyone for anything. However, since advertisers have a long history of talking about a power amplifier’s capabilities in terms of watts, the tradition continues, regardless of its irrelevance. On the other hand, if you’re buying a toaster, the power consumption is a great thing to know…

* I’m pretending for this posting that a loudspeaker driver acts as a resistor to keep things simple. It doesn’t – but I’m not going to talk about phase or impedance today.

P.S. Yes, I cut MANY corners and oversimplified a LOT of issues in this posting – I know. Don’t send me hate mail because I didn’t mention reactance or crest factor…

What’s a woofer?

#82 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Occasionally, a question that comes into the customer communications department to Bang & Olufsen from a dealer or a customer eventually finds its way into my inbox.

This week, the question was about nomenclature. Why is it that, on some loudspeakers, for example, we say there is a tweeter, mid-range, and woofer, whereas on other loudspeakers we say that we’re using a “full range” driver instead? What’s the difference? (Folded into the same question was another about amplifier power, but I’ll take that one in another posting.)

So, what IS the difference? There are three different ways to answer this question.

Answer #1: It’s how you use it.

My Honda Civic, the motorcycle that passed me on the highway this morning, and an F1 car all have a gear in the gearbox that’s labelled “3”. However, the gear ratio of those three examples of “third gear” are all different. In other words, if you showed a mechanic the gear ratio of one of those gearbox settings without knowing anything else, they wouldn’t be able to tell you “ah! that’s third gear…”

So, in this example, “third gear” is called “third” only because it’s the one between “second” and “fourth”. There is nothing physical about it that makes it “third”. If that were the case then my car wouldn’t have a first gear, because some farm tractor out there in the world would have a gear with a lower ratio – and an F1 car would start at gear 100 or so… And that wouldn’t make sense.

Similarly, we use the words “tweeter”, “midrange”, “woofer”, “subwoofer”, and “full range” to indicate the frequency range that that particular driver is looking after in this particular device. My laptop has a 1″ “woofer” – which only means that it’s the driver that’s taking care of the low frequencies that come out of my laptop.

So, using this explanation, the Beolab 90 webpage says that it has midranges and tweeters and no “full range” drivers because the midrange drivers look after the midrange frequencies, and the tweeters look after the high frequencies. However, the Beolab 28’s webpage says that it has a tweeter and full range drivers, but no midranges. This is because the drivers that play the midrange frequencies in the Beolab 28 also play some of the high-frequency content as part of the Beam Width control. Since they’re doing “double duty”, they get a different name.

Answer #2: Excruciating minutiae

The description I gave above isn’t really an adequate answer. For example, I said that my laptop has a 1″ “woofer”. Beolab 90 has a 1″ “tweeter” – but these two drivers are not designed the same way. Beolab 90’s tweeter is specifically designed to be used to produce high frequencies. One consequence of this is that the total mass of the moving parts (the diaphragm and voice coil, amongst other things) is as low as possible, so that it’s easy to move. This means that it can produce high frequency signals without having to use a lot of electrical power to push it back and forth.

However, the 1″ “woofer” in my laptop is designed differently. It probably has a much higher total mass for the moving parts. This means that its resonant frequency (the frequency that it would “ring” at if you hit it like a drum head) is much lower. Therefore it “wants” to move easily at a lower frequency than a tweeter would.

For example, if you put a child on a swing and you give them a push, they’ll swing back and forth at some frequency. If the child wanted to swing SLOWER (at a lower frequency), you could

  • move to a swing with longer ropes so this happens naturally, or
  • you can hold on to the ropes and use your muscles to control the rate of swinging instead.

The smarter thing to do is the first choice, that way you can keep sipping your coffee instead of getting a workout.

So, a 1″ woofer and a 1″ tweeter are not really the same thing.

Answer #3: Compromise

We live in a world that has been convinced by advertisers that “compromise” is a bad thing – but it’s not. Someone who does never accepts to compromise is destined to live a very lonely life. When designing a loudspeaker, one of the things to consider is what, exactly, each component will be asked to do, and choose the appropriate components accordingly.

If we’re going to be really pedantic – there’s really no such thing as a tweeter, woofer, or anything else with those kinds of names. Any loudspeaker driver can produce sound at any frequency. The only difference between them is the relative ease with which the driver plays a signal at a given frequency. You can get 20 Hz to come out of a “tweeter” – it will just be naturally a LOT quieter than the signals at around 5 kHz. Similarly, a woofer can play signals at 20 kHz, but it will be a lot quieter and/or take a lot more power than signals at 50 Hz.

What this means is that, when you make an active loudspeaker, the response (the relative levels of signals at different frequencies) is really a result of the filters in the digital signal processing and the control from the amplifier (ignoring the realities of heat and time…). If we want more or less level at 2 kHz from a loudspeaker driver, we “just” change the filter in the signal processing and use the amplifier to do the work (the same as the example above where you were using your muscle power to control the frequency of the child on the swing).

However, there are examples where we know that a driver will be primarily used for one frequency band, but actually be extending into another. The side-facing drivers on Beolab 28 are a good example of this. They’re primarily being used to control the beam width in the midrange, but they’re also helping to control the beam width in the high frequencies. Since, they’re doing double-duty in two frequency ranges, they can’t really be called “midranges” or “tweeters” – they’d be more accurately called “midranges that also play as quiet tweeters”. (They don’t have to play high frequencies loudly, since this is “only” to control the beam width of the front tweeter.) However, “midranges that also play as quiet tweeters” is just too much information for a simple datasheet – so “full range” will do as a compromise.

P.S.

I’ve got some extra things to add here…

Firstly, it has become common over the past couple of years to call “woofers” “subwoofers” instead. I don’t know why this happened – but I suspect that it’s merely the result of people who write advertising copy using a word they’ve heard before without really knowing what it means. Personally, I think that it’s funny to see a laptop specified to have a “1” subwoofer”. Maybe we should make the word “subtweeter” popular instead.

Secondly, personally, I believe that a “subwoofer” is a thing that looks after the frequency range below a “woofer”. I remember a conversation I had at an AES convention once (I think it was with Günther Theile and Tomlinson Holman) where we all agreed that a “subwoofer” should look after the frequency range up to 40 Hz, which is where a decent woofer should take over.

Lastly, if you find an audio magazine from the 1970s, you’ll see that a three-way loudspeaker had a “tweeter”, “squawker”, and “woofer”. Sometime between then and now, “squawker” was replaced with “midrange” – but I wonder why the other two didn’t change to “highrange” and “lowrange” (although neither of these would be correct, since all three drivers in a three-way system have limited frequency ranges).

Telefunken Lido: Repair (Day 6)

Day 5’s work can be seen here.

So, it was obvious that the speed regulation wasn’t working properly at the end of Day 5. So, last night was spent digging for information on how centrifugal speed governors work and I came across this excellent explanation.

So, my theory was that the disc was seized on the axle and not moving correctly with the rotational speed. This means that everything came apart again, and the axle had to come out.

In theory, as the governor spins faster, the three weights get pulled out. This in turn should pull the disc in to rub against the friction pad. When it came out of the motor, the disc was immovable – it was stuck to the axle as I guessed. So, the three springs+weights were removed from the axle and, after a lot of WD-40 and a little repeated gentle “persuasion”, I got to here:

This is after I polished the rust off the axle with sandpaper, starting at 400 and working up to 3200 (lubricated with more WD-40). I was sanding along the length of the axle, since that’s the direction of movement of the disc.

Then it was “just” a matter of putting it all back together again… However, before I put it back in the case, I checked that the governor was working, which you can see below. Notice how the disc moves sideways to meet the friction pad, keeping things at a constant speed.

Then it was just a matter of putting everything back together again… And I have a working Telefunken Lido for those Sunday afternoon garden parties!