So, you just bought a subwoofer and it has a bunch of controls on it with some familiar names like “level” or “gain”, some sort-of-familiar ones like “cutoff frequency” and “phase” (or, more correctly “polarity” or maybe a switch that says “invert”), and possibly a really unfamiliar knob that says “phase” or “all pass” that goes from a low number to a high number (maybe).

What do all of these controls do, and how do you adjust them?

Well, let’s start with a simple system. We have one subwoofer, one main loudspeaker (let’s say, the left front one) and a “crossover” that divides the energy in the frequency bands appropriately and correctly (in other words, it splits up the bass and the mid/treble and sends the lower stuff to the sub and the upper stuff to the main loudspeaker). Let’s also start with a situation where the subwoofer and the main loudspeaker are the same distance from you, the listener. They’re both set to the correct gain. Everything else in the system is perfect, and you are outdoors (that way, there are no nasty room acoustics to screw us up).

The result of all of this, at the listening position, will be something like the figure below. The black curve shows the output of the subwoofer. (I’ve limited its output to 120 Hz – a typical value – but as you can see, it has lots of output above 120 Hz – it just gets lower and lower in level as you go higher and higher in frequency.) The blue curve shows the output of the main loudspeaker, with a lower limit of 120 Hz. The red curve shows the result of the two of the curves being added together. Note that I have not just added the black and the blue curves. I have actually added the two outputs plotted the result as a frequency response.

Now, let’s change one little thing. We’ll leave everything untouched except for the GAIN (or LEVEL or VOLUME) knob on the subwoofer. Let’s start by turning that up by 6 dB. This means that you now have twice as much sound pressure from the subwoofer. The result will not come a a surprise. As you can see in the red graph below, you get more bass. In fact, you get 6 dB more bass. So, if you like more bass (and you don’t have neighbours), then this is a good idea.

Similarly, we can leave everything untouched except for the GAIN (or LEVEL or VOLUME) knob on the subwoofer and turning it down by 6 dB. This means that you now have half as much sound pressure from the subwoofer. As you can see in the red graph below, you get less bass. In fact, you get 6 dB less bass. So, if you don’t like more bass (or if you have cranky neighbours or sleeping children), then this is a good idea instead.

Okay, enough of the easy stuff. Let’s get complicated. Let’s set the gain of the subwoofer back to “correct” and move the subwoofer away a little bit. We’ll start by moving it 1.433 m (that’s about 4′ 8 1/2″ for those of you in the USA…) further away from the listening position than the main loudspeaker (I have chosen this value carefully, but it doesn’t matter how, for the purposes of this discussion…) Now, without fiddling with any of the knobs, what do we get at the listening position? Well, that will look like the figure below.

There are two important things to notice in the plot above. The first thing is that the black and blue curves are identical to the ones in the plot at the top. This means that the individual outputs of the subwoofer and the main loudspeaker have the same frequency content as they did when we started. This should not come as a surprise, since all we did was to move the subwoofer – it should have the same output. The second thing to note is that there is now a big dip in the red curve at 120 Hz. Why is this? Well, it’s because when the two loudspeakers have a difference in distance of 1.433 m, they don’t line up in time. The practical result of this is that, at 120 Hz, both of the loudspeakers “push” air at the same time, and that high pressure in the air starts moving towards you. A little while later, both loudspeakers (which is closer to you) are “pulling” air, making a low pressure in the air. The problem is that, due to the speed of sound being “only” 344 m/s, the amount of time it takes the high pressure to get from the subwoofer to the main loudspeaker (1.433 m away…) is exactly the same amount of time it takes for both speakers to change from “pushing” to “pulling”. So, when the high pressure from the subwoofer passes by the main loudspeaker, the main loudspeaker is creating an equal (but opposite) low pressure. Those two pressures (one high and one low) add together in the air and cancel each other out. As a result, you can think that the output of the main loudspeaker counteracts the output of the subwoofer, and you get less.

The important thing to remember here is that both speakers are working just as hard as they did before – it’s just that you don’t get any output at that one frequency. Note as well that the frequency where the subwoofer and the main loudspeaker cancel each other is dependent on how far apart they are, as we’ll see later.

What does this sound like? Well, you might notice that there are a couple of bass notes (specifically, around the B a little more than an octave below middle C) are much quieter than the other bass notes. Or, you might just experience that you have less bass generally. For those of you who think that “bass” is much lower than 120 Hz, you might experience that the total system loses warmth in the sound (although “warmth” is generally a little above 120 Hz… depending on your tastes…)

So, how do we fix this problem? Well, since we have a problem with high pressures getting cancelled by low pressures, one solution is to “flip” the output of the subwoofer so that it generates a low instead of a high and vice versa. (In other words, we’re telling it to “push” out instead of “pulling” in and vice versa. We can do that by changing the POLARITY or PHASE  or Ø switch (those are just different names for the same thing – sort of…) on the subwoofer to NEGATIVE or INVERT. The result of this, at the listening position, is shown below.

As you can see in that plot above, the result isn’t perfect, but it’s a lot better. The deep notch that we had at 120 Hz is gone, and now all we have is a little ripple around the “crossover region” where the outputs of the two loudspeakers overlap.

There are some people who think that there is an audible difference between the sound of a kick drum “pushing” a loudspeaker out (and making a high pressure) and “pulling” a loudspeaker in (and making a low pressure) and, as a result, they don’t like flipping (or inverting) the polarity of a subwoofer. If you’re that kind of person, and if you have a PHASE or ALLPASS knob on your subwoofer, you have an option. An allpass filter is a special filter that does not change the magnitude (or output level) of the signal, but it does change the phase as a function of frequency. What that means (sort of) is that it can add (or subtract) different delays for different frequencies (I know, I know, it’s not a delay – but if you can think of a better way to describe it to neophytes, be my guest). If we use an all pass filter (for the geeks, I’m using a second-order allpass filter) and set its frequency to 120 Hz and apply that to the subwoofer signal, the result is shown in the plot below.

In other words, if you have a problem like this, and you flip the polarity switch and get those missing bass notes back (or the bass in general – or the warmth), then you’ve probably fixed the problem.

As you can see in that plot above, the result still isn’t perfect. In fact, it’s a little worse than the polarity invert solution – but it’s still a lot better than the problem we’re solving. The deep notch that we had at 120 Hz is gone, and now all we have is a little (but slightly bigger) ripple around the “crossover region” where the outputs of the two loudspeakers overlap.

The reason this particular setting of the allpass filter worked is because I had a 2nd order allpass filter, and I set it to 120 Hz. This meant that the phase “delay” of the allpass filter was the same as the phase “delay” caused by the difference in distance. If I had used an allpass filter with a different order (i.e. a 1st order), and/or a different frequency, and/or a different distance, this would not have worked as well (we’ll see that as an example below…).

So, the moral of the story here is that, if you have the problem caused by distance, and you play with the ALLPASS or PHASE knob, and listen to those missing bass notes, just fiddle with the knob until the bass notes are there…

But what happens if the subwoofer is further away than the main loudspeaker but not as far away as we have been looking at above? Let’s place the subwoofer 0.72 m (2′ 4 1/4″) further away than the main loudspeaker and take a look at the result – shown in the red plot below.

Now you can see that we still have a dip at 120 Hz, but it’s not as bad as when the subwoofer was 1.4 m away. This is because the time alignment of the two loudspeakers is better, the closer together they are.

So, how do we solve this problem? Well, let’s start by flipping the POLARITY switch again. The result of that is shown below.

As you can see in the red plot above, flipping the POLARITY or INVERT switch actually makes the problem worse now that the loudspeakers are closer together. We’re losing more “bass” at 120 Hz because we have flipped the switch. So, we’ll need to find a different solution.

Okay, let’s play with the allpass filter again. We’ll set it to 120 Hz like we did before and take a look at the result (shown below).

Hmmmm… that didn’t work. Not only is the allpass (at 120 Hz)  worse than the original problem, it’s also worse than flipping the POLARITY switch (in other words, we’ve lost more bass around 120 Hz – since the dip in the red curve is deeper).

Okay, let’s fiddle with that ALLPASS or PHASE knob a little. we’ll start by turning it lower in frequency, the result of which is shown below.

Hey, that worked well! Although our problem is at 120 Hz, we nearly fixed the problem by setting the allpass filter’s frequency to 40 Hz. Again, a different order of allpass, or a different distance between loudspeakers or a different anything else would have resulted in us finding a different frequency. Do not assume that 40 Hz is the magic number.

Just because I like fiddling with knobs, let’s try going the other way. We’ll turn up the allpass frequency to 240 Hz – the result of which is shown below.

Hmmmm.. .that’s not good. We’ve made the problem much worse. Okay – set it back to 40 Hz (for this example…).

The moral of the story

If you go to a lot of websites, you’ll get the advice that, when setting up a subwoofer, you should put the speakers where you want them, and then fiddle with the switches and knobs so that you get the most bass. This is only partly true. As you can see above, we’re really talking about a frequency band around the “crossover region” where the signals are coming from both the subwoofer and the main loudspeakers.

In a perfect world, the subwoofer has characteristics that perfectly match the main loudspeakers, and you’ve put all of them the same distance from the listening position. This is rarely true. So, you’ll have to fiddle with something to clean up the resulting mess. However, if you just listen for “bass” you might be distracted away from where the real problem lies. Instead, set up your system and listen to the bass line (i.e. the notes played by the instrument called the bass – I don’t care if it’s electric or acoustic. If you prefer ‘celli, you can use them instead). If you notice that some notes are much quieter, you have a problem that you might be able to fix by fiddling with the subwoofer’s controls. Take them one at a time, and listen to those notes that you lost before. If you get them back, you’ve fixed the problem. If you fiddle with every knob, and you can’t get those notes, you might need to blame the musicians or the recording engineer… In fact, it will have to be their fault, because if it’s not, it might be your room, and fixing that is expensive.

Typically, when you read a review of a loudspeaker, you’ll often see a graph that shows a measurement of its “frequency response”. This is a measurement of how loud the loudspeaker is at different frequencies at one position, directly in front of it, if you feed the same signal level into the input of the loudspeaker, and you are not in a room with reflecting surfaces. Usually a measurement like this is done by placing a microphone 1 m in front of the tweeter and putting some special signal (like a sine wave with a changing frequency or something called an MLS signal) into it. In (some persons’ ) theory, the goal of a loudspeaker is to have exactly the same output level at all frequencies (assuming that all those frequencies went into it at the same input level). In other words, output equals input.

However, that’s only a very small view of reality. For starters, this measurement is only done at one signal level. There is no guarantee that the loudspeaker will behave the same way if you measured it with a louder (or a quieter) signal. However, for the purposes of this discussion, we’ll take issue with another point. One big problem with this measurement is that it only tells you how the loudspeaker behaves at one point in space – and this is simply not enough information.

In reality, sound does not beam out of the front of a loudspeaker like a laser beam. The truth is that sound comes out of the loudspeaker and heads in all directions – left, right, up, and down. So, one question to ask is “what’s the difference in the sound that goes out the front, and the sound that goes out the side or the back?” Well, generally speaking – and this is VERY general – there is less and less energy in the high frequencies as you come around to the back of the loudspeaker. There are physical reasons for this that we’ll talk about later (or you could go look it up now, if you prefer) but we won’t get into it here.

So, let’s take a very simplified example:

Let’s say that the plot shown above is a frequency response measurement of a loudspeaker done directly in front of it, “on-axis” to the tweeter, 1 m away. As you can see, it has an unbelievably flat frequency response (I’m faking it…) with a roll-off in the very low end (50 Hz) and the high end (18 kHz). How would the same loudspeaker measure if we were to put the microphone at the same distance, but directly to one side,  90° off-axis? Well, it might look  something like this:

You’ll note here that the low end roll-off hasn’t changed – we have just lost high frequencies. Now let’s measure again, but this time, we’ll put the microphone directly behind the loudspeaker. In this case, we might see a frequency response measurement that look something like this:

So you can see there that we have the same effect – just more of it.

So, the first moral of the story here can be read two different ways:

Option 1: The further around the back of the speaker you go, the less high frequency information you’ll get – or at least, the quieter the high frequencies will be.

Option 2: Bass goes everywhere equally, but high frequencies tend to “beam” forwards.

But there is a different moral to be learned here. Usually, when you buy a lamp to hang on the ceiling to light up a room, you don’t think about how much light is beaming straight out of it, down towards one point on the floor or the wall. Usually, you think about how much light goes out in all directions at the same time – how much it lights up the room (instead of just one location in the room). The same is true for a loudspeaker. We can think about how much energy is coming out of the loudspeaker in all directions at the same time – in other words, how much energy is going out into the room, and not just what’s headed toward your left ear.

In order to consider this, we have to add up the frequency responses of the loudspeaker going out in all directions at the same time. For the purposes of this discussion, we’ll pretend to do only 3 measurements – for the front, side, and back of the loudspeaker – but let’s say that’s enough for now. If we add up the energy in the three frequency responses we saw above, we’ll get something like the one below:

On that plot shown above, you can see the three original measurements, and the result when you add the three of them together (the red curve). In our simplified little world here, what this shows is that, if you consider the sound coming out of the loudspeaker in all directions at the same time (the red curve) you can see that there is more energy in the low frequencies than the high frequencies. So, if we normalised the two measurements (in other words, make them comparably loud (in other words, align them vertically on the graph)) and compare them directly, we see the plot show below, which shows that the power response is generally more bass-y than the frequency response.

So what? Well, if you turn on the music in the living room, and you head into the kitchen to make dinner, you aren’t on-axis to the loudspeakers. So the sound that you’re hearing has very-little-to-nothing to do with the black curve. What’s actually happening is that the sound radiates out of the loudspeaker in all directions at the same time, bounces around the living room and leaks into the kitchen. So, what you’re listening to has much more to do with the red curve than the black curve. If we were being more geeky, we would say that you’re listening to the loudspeaker’s “power response” (because we’re talking about the sum of the total acoustic power put into the living room) instead of its “frequency response”.

That doesn’t necessarily mean that you should try to build a loudspeaker  with a flat power response – that’ll sound really bright. However, it might mean that the frequency response curve you see in the magazine review isn’t the only thing that you should worry about… It also means that if you’re building a speaker for people  who have more than one chair in the house (or people who have friends), you might want to worry about something more than just the frequency response.

And, just in case you think that I’m oversimplifying too much here, let me prove to you that I’m not. The plots above were built on fake curves, showing what happens when I add only three measurements of a loudspeaker, one in the front, one in the side and one in the back of the device. However, take a look at the curves below. These are two real measurements of a real loudspeaker. The blue curve is the on-axis frequency response measurement (note that this is an active loudspeaker that has been equalised to have a flat-ish on-axis frequency response). The red curve is the measured power response of the same loudspeaker which was found by making a LOT of frequency response measurements around the loudspeaker and summing the results all together to get an idea of what the device was doing in all three dimensions. Looks pretty similar to the fake plot above, doesn’t it?

So, you want to build a loudspeaker…

One of the questions you’ll probably be asking yourself is whether you want to build a ported loudspeaker (sometimes called a “bass reflex” loudspeaker) or one with a sealed enclosure. If you want to know the general reasons why most people think that you should choose one or the other, go somewhere else for information – or maybe come back here later (maybe I’ll talk about it in a later posting).

For this posting, I want to look at a couple of things that I haven’t seen elsewhere – mostly because it helps me to understand the difference between ported and sealed loudspeaker enclosures a little better.

Let’s take a loudspeaker driver and put it in a box. For the purposes of this discussion, we’ll simulate a 10″ driver with mostly-real Thiele-Small parameters in a simulated sealed box. The box has a volume, but we’ll leave out any possible internal modes to keep things simple for now. We’ll also ignore additional effects such as diffraction – we’re just looking at the how the enclosure’s volume and the port dimensions affect the response of the system.

If we sweep a sine wave into the driver, keeping the voltage constant, and we measure the sound pressure level in front of the driver, we’ll see that the total system (the loudspeaker in a sealed box) acts as a minimum phase, second-order high pass filter. Therefore it has a rising slope of 12 dB/octave in the low end. The Q of that high-pass filter will be dependent on the relationship of the driver’s parameters and the size of the box.

In the plots above, you can see the results on the magnitude response of changing the enclosure volume. The blue curve on the far left is the response you’d get from putting the driver in an infinite baffle (actually, I simulated an enclosure of about a cubic kilometre or so… So not quite infinite, but pretty big for a woofer cabinet…). Notice that it has the highest output at the lowest frequency, but you don’t get as much output around the knee as you do with the other curves. As the enclosure volume is made smaller (The green curve is 1000 litres, and each curve after that, moving left to right, is for a volume of one-half the previous one, so, 500 l, 250 l, 125 l, 62.5 l, 31.25 l, and 15.625 l. Remember – the driver that we’re simulating here isn’t real, so don’t worry about the actual volumes – we’re just worried about the differences in magnitude response as the volumes get smaller.)

You can see in the plots that, by making the volume behind the driver smaller, we do a couple of things at the same time.

1. One is that, the smaller the enclosure, the higher the cutoff frequency of the resulting high pass filter. This is because the “spring” supplied by the air in the enclosure gets stiffer (or less compliant) as the box gets smaller, so it rings at a higher frequency.
2. Secondly, you’ll notice that the Q of the high pass filter increases as the enclosure gets smaller. This is because the damping factor of the total system (which is, in turn inversely related to the Q – the lower the damping, the higher the Q) decreases as the spring gets stiffer ( and the compliance goes down), if neither the mass nor the losses in the system change.

Both of these are basically the same as having a series RLC circuit and decreasing the capacitor value. The resonant frequency will go up, and the damping factor will go down.

Now, what happens if we wanted to build a ported loudspeaker instead? For now, let’s just use the same loudspeaker driver, a 1000 litre enclosure and we’ll add a port. We’re keeping it simple, so we will just add the port as a pipe sitting outside the enclosure so it doesn’t take away from the enclosure’s volume. Also we will not include the port’s volume as part of the enclosure volume. Also, because this isn’t the real world, we’ll make the port’s output in the same physical location as the loudspeaker driver to avoid any problems with propagation delay and interference at the microphone location.

The above plots show the result of this imaginary ported box with different port lengths, keeping all other parameters constant. I’ve made the losses in the port low so that the port has a bigger contribution to the total magnitude response, and therefore is easier to see. Remember – we’re not simulating the real world – we’re intentionally making the simulation produce curves that show patterns to better understand what’s going on. The ports that I’ve simulated are 10 cm in diameter, and have a length of (again from left-to-right) 1.6 m, 800 cm, 400 cm, 200 cm, 100 cm, 50 cm, 25 cm, and 12.5 cm.

What can we see in these plots?

1. Firstly, you can see that the slope of the high pass filter is now steeper than it was with the closed cabinet. This is because a ported loudspeaker enclosure results in a fourth-order high-pass system, so we have a slope of 24 dB/octave. This means that, in the very low end, we have a LOT less output from the ported system than the sealed system.
2. Secondly, you can see that, in this case, changing the port length has an puts a bump in the output’s magnitude response around a frequency that is dependent on the port length. The longer the port, the lower the centre frequency of the bump. This isn’t a surprise, since making the port longer lowers the resonant frequency of the Helmholtz resonator. In real life, the bump probably wouldn’t be as prominent – I made it obvious by simulating a port with very low losses (Those losses are the result of things like turbulence around the ends of the port and friction where the air “plug” in the port is rubbing against the sides of the port and the energy is converted to heat.)
3. Thirdly, you will see that the cutoff frequency of the system doesn’t change as much as it did when I was changing the volume of the sealed enclosure.

So, how do these systems compare? You’ll often hear people say “I chose to make a bass reflex loudspeaker so that I would get more bass out of the system.” The question is, does this sentence make sense? Is this really a good reason to choose a ported enclosure over a sealed one when you’re building a loudspeaker? Let’s look at what magical wonders adding a port had brought to our pretend loudspeaker…

The above plots show the difference in the output of the systems, showing the relative outputs of the ported systems (the colours are arranged to be the same as the ones in the previous plot so you know which port is which length) compared with the same enclosure without a port (in other words, the green curve from the top plot). Basically, all I’ve done here is subtracted the green curve from the top plot from all the curves in the second plot. If the result is 0 dB (as it is in the high frequency region for all of the curves, then this means that the two systems have the same output. If the value for a given frequency is positive, then this means that the ported system is louder than the sealed system. If the value is negative, then it means that the ported system is quieter by that amount.

As can be seen in that plot, there is a frequency region for all ported systems where you get more output for the same voltage. In the high end, both systems give the same output (because that’s so far above the port resonance that it’s basically not a part of the system, so they both behave the same way). In the low end, the ported system gives much less output because it’s a 4th-order high pass instead of a 2nd-order high pass like the sealed enclosure system.

So far, we can see that a ported system does appear to give you more bass for the same input voltage, assuming that you’ve tuned the port to give you more output in a band that you call bass – however, below that band, you get less. So you might be “robbing Peter to pay Paul” – which might not necessarily be a good idea.

Some people (who might know a little more about what they’re talking about than the last people I mentioned) say “I’m going to build a bass reflex loudspeaker instead of a sealed system to reduce distortion in the driver at the port resonance.” Now why on earth would they say that? Well, a little more digging (not much more digging, admittedly) will turn up an extra little piece of information: the driver moves less at frequencies around the port resonance. For example, at the resonant frequency of the port, the Helmholtz resonator acts against the driver, pushing it out when it tries to move in and pulling it in when it tries to move out. As a result, the excursion of the driver drops. In an extreme (non-real-world) case, if there are no losses in the port or the enclosure, then the driver’s excursion would be 0 at the port resonance. The greater the losses, the less this will be true.

So, let’s check out our two systems again, this time, looking at the driver excursion (peak excursion, to be precise) by frequency.

The above plot shows the peak excursion of the driver in the sealed cabinet. The colours correspond directly to the curves in the first plot at the top of the posting so that you can see the kind of magnitude response you get for the excursion. As you can see, in all cases, the excursion of the driver in the high frequency region is nearly 0 mm – the higher we get, the closer we get to 0 mm. You can also see that, in the low end, the excursion levels out. The more level the excursion plot, the closer the slope of the magnitude response is to a “perfect” 12 dB/octave. This is because the sounds pressure only comes from the air moved by the driver, and because the sound pressure level is proportional to the acceleration of the driver. As the frequency drops and the excursion stays the same, the acceleration drops by 12 dB per halving of frequency because it’s the derivative of the velocity which drops by 6 dB per halving of frequency, because it’s the derivative of the excursion in time.

Of course, if your driver can’t handle the excursions we see here (for example, the one I’m using for this simulation can only move 8 mm before it starts to get unhappy) then you might have something to worry about here. How you deal with that problem, however, is your problem.

So, what would the excursion look like for the same driver in a ported cabinet? Let’s have a look!

The plot shown above has the peak excursion curves for the same driver in the ported cabinet for the port lengths listed high above… As you can see, starting at the top end, the excursion of the driver is nearly 0 mm, just as in the case of the sealed cabinet. As the frequency drops, the excursion starts to increase. However, then something weird happens. Going lower in frequency, we can see that the driver excursion levels out and starts to drop, with a minimum value at the resonance of the port. If you’re very attentive, you’ll notice that this frequency isn’t exactly the same as the frequency of the bump in the total system’s magnitude response. That’s not a big surprise, since there is some other frequency (in this weird, non-real-life system) where the summed outputs of the driver and port give you more output than they do at the port resonance (actual results may vary). Anyway, going below the port resonance, you can see that the excursion of the driver really takes off and becomes much greater than it was with the sealed system. That’s because there’s nothing there to stop it. At frequencies that are much lower than the port resonance, the system behaves as if the driver wasn’t in a box at all, so it’s free to move as far as it wants to go. (remember that our non-real-life system isn’t limited by things like the maximum excursion of the suspension… The values in the plot show the excursion that the driver “wants” to hit – it’s just held back by real life.)

So, you may be asking yourself a question at this point: “Why is it that, at very low frequencies, the driver’s excursion is much higher in the ported system than in the sealed system, but you get less output?” Good question! The reason is that, at frequencies far below port resonance, you get almost as much output from the port as the driver. The only problem is that the port is just delivering the pressure at the back of the driver to the outside world. So, when the front of the driver goes positive, the back of the driver (and therefore the port) goes negative, and the two cancel each other at the listening position. Putting the port opening at the back of the loudspeaker won’t help much. It will just make the propagation distance a little longer, therefore a little later, but they’ll still cancel each other. This is why the total output of the ported system drops faster as you go lower in frequency – the lower you go, the more the driver and the port cancel each other. They’re both working really hard (and therefore, so is your amplifier), but you get next-to-nothing.

However, let’s back up a bit. There is that issue of the lower driver excursion around the port resonance. This is true. So, if you have a loudspeaker driver that doesn’t like excursion (maybe, say, it distorts when it moves to far) in a particular frequency band, then maybe a port could alleviate the problem. However, beware of frequencies below! Danger danger! (In other words, you might want to put a high pass filter in your system to keep things running smoothly below the port resonance…)

A couple of plots ago, we did some subtraction to compare the magnitude responses of the ported systems to a sealed system. Let’s do the same for the excursion plots. The above figure shows the difference between the peak excursion of the driver in the ported systems, and that of the driver in a sealed enclosure of the same volume. Negative values mean that the ported cabinet driver moves less than the sealed cabinet one. Positive values mean that the ported cabinet driver moves further than the sealed cabinet one.

As you can see in those curves, in the high frequencies, the driver will have the same excursion in both cases. Secondly, there is some region in all cases where the driver moves less in a ported system than in a sealed cabinet of the same volume. At low frequencies, the ported cabinet driver moves further than the sealed cabinet equivalent (yet has less total output, remember!). An interesting detail to note here is to look carefully at this plot with the magnitude difference plot. For example, take a look at the left-most blue curve. The ported system driver has a lower (or equal) excursion than the sealed system driver from about 6.5 Hz and up. Looking at the magnitude response difference curve for the same system, we can see that we get about 6 or 7 dB more output from the ported system at 6.5 Hz, with less and less benefit as we go higher in frequency. Below 6.5 Hz, although we get more output from the ported system for about an octave, it comes at the cost of a much greater excursion, which would probably not be good for our driver.

So what?

Okay, let’s be honest here. I’ve made two very simulated systems, and only changed one variable in each system to see what happens. And, I can absolutely guarantee that (1) no loudspeaker driver in the world has the parameters of the one I’ve simulated and (2) if you built the system I’ve simulated, it wouldn’t behave as I’ve shown here. This is a very isolated, idealised simulation, intentionally designed to make the changes I was making obvious. However, the issues that I’ve made obvious are basically true – I’ve just done a little exaggeration…

What’s the moral of the story? Well, I’m not really sure of all of them. One moral is certainly “sticking a port on a loudspeaker enclosure is not a free ticket to more bass”. Another moral is “people who use ports to reduce driver excursion might not know what they’re talking about”. Probably the most important moral is “don’t trust everything you read” – even the stuff you read here.

Post Script

If you REALLY want to learn this stuff correctly, go read the following:

Closed Box Loudspeaker Systems – Part 1: Analysis

Closed Box Loudspeaker Systems – Part 2: Synthesis

Vented Box Loudspeaker Systems – Part 1: Small Signal Analysis

Vented Box Loudspeaker Systems – Part 2: Large Signal Analysis

Vented Box Loudspeaker Systems – Part 3: Synthesis

Vented Box Loudspeaker Systems – Part 4: Appendices

When you’re done with those, please explain them to me.

So, you want to build a loudspeaker…

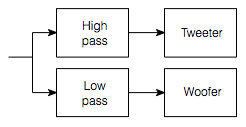
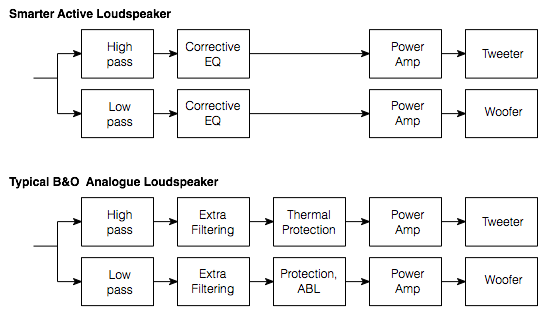
One of the first things you’ll find out is that, if you’re building a loudspeaker with moving coil drivers, and unless you want a loudspeaker with very limited capabilities, you’ll probably need to use more than one driver. Starting small, you’ll at least need a bigger driver to produce the lower frequencies and a smaller driver to produce the higher ones. No surprise so far – many people lead meaningful lives with just a tweeter and a woofer.

However, you’ll probably need to ensure that the tweeter doesn’t get too much signal at low frequencies, and the woofer doesn’t get too many highs. In order to do this, you’ll need a crossover. Still no surprises. Most people who build a loudspeaker already know that they’ll need a crossover to keep their drivers happier.

Now for some new stuff – at least for some people. When you make a crossover, you must remember to keep the driver’s characteristics in mind. You can’t just slap a high pass filter on the tweeter and a low pass filter on the woofer and expect things to work. The tweeter is already behaving as a high pass filter all by itself. If the characteristics of the tweeter’s inherent high pass are what you want, then you don’t want to duplicate that filter in the electronics. So, design your filters wisely. I will probably come back to some examples of this some time in a future posting.

However, that is not the topic for today. For today, we will assume that we are building a loudspeaker using two very special drivers. They are:

1. infinitely small
2. have bandwidths that go from DC to infinity
3. have “perfect” impulse responses
4. and therefore have completely flat phase responses

In other words, we will pretend that each of our drivers is a perfect point source. We’ll also assume that they are not mounted on a baffle (a fancy way of saying “on the front of a box” – usually…). Instead, they’re just floating in space, arbitrarily 25 cm apart (one directly above the other). We’ll arbitrarily make the crossover frequency 500 Hz. Finally, let’s say that we’re arbitrarily 2 m away from the loudspeaker.

The reason for all of these assumptions is that, for the purposes of this posting, we’re only interested in the effects of the crossover on the signal, so I’m making everything else in the system either perfect or non-existent. Of course, this has nothing to do with the real world, but I don’t really care today.

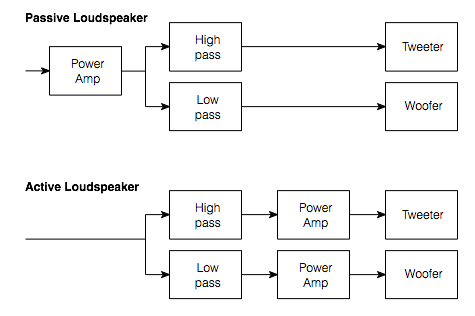
So, if you’ve done a little research, you’ll know that there are a plethora of options to chose from when it comes to crossovers. I’ll assume that we’re building an active loudspeaker with a DSP so we can do whatever we want.

Linkwitz Riley, 4th Order

Let’s start with Old Faithful: a 4th-order Linkwitz-Riley crossover. This is implemented by putting two 12 dB/oct Butterworth filters in series, each with a cutoff frequency equal to the intended crossover frequency. (If you’re using biquads, set your Q to 1/sqrt(2) on each filter). The total low pass section will have a gain of -6.02 dB at the crossover frequency (so will the total high pass section). Since the two sections are 360° out of phase with each other at all frequencies, they’ll add up to give you a total of 0 dB when they sum together at any frequency. However, you must remember that the filter sections used in the crossover have an effect on the phase response of the re-combined signal. As a result, when the two are added back together (at the listening position) the total will also have a modified phase response – even when you are on-axis to the loudspeakers, (and equidistant to the two loudspeaker drivers).

It is also important to remember that the phase relationship of the two sections (coming from the tweeter and the woofer) is only correct when those two drivers are the same distance from the listener. If the tweeter is a little closer to you (say, because the tweeter is on top and you stood up) then its signal will arrive too early relative to the woofer’s and the phase relationship of the two signals will be screwed up, resulting in an incorrect summing of the two signals.

How much the total is screwed up depends on a bunch of factors including

1. the relative phase responses of the filters in the crossover
2. the phase responses of the drivers (we’re assuming for this posting that this is not an issue, remember?)
3. the deviation in those phase responses caused by the mis-alignment of distances to the drivers

The result of this is a deviation in the vertical off-axis response of the loudspeaker. How bad is this? Let’s look!

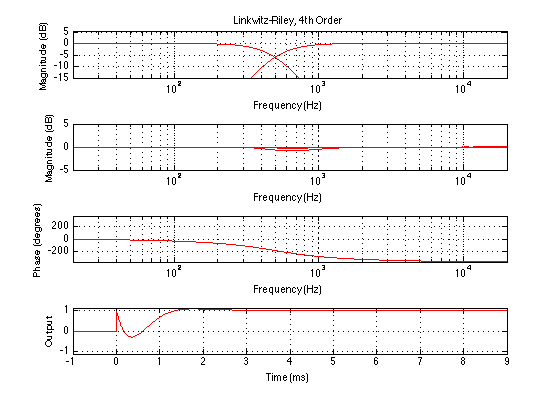
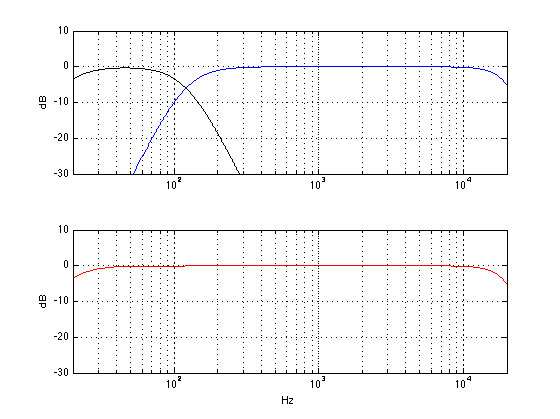
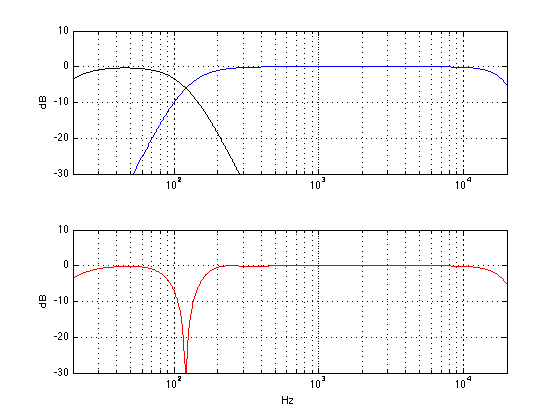
This figure shows 4 plots. The top one shows the magnitude responses of the two individual sections. As you can see, the crossover frequency is 1 kHz, and both sections are 6 dB down at that frequency.

The second plot shows the total magnitude responses at 5 different vertical angles of incidence to the loudspeaker: -30°, -15°, 0°, 15°, and 30°. So, we’re going from below the loudspeaker to above the loudspeaker. It’s not obvious which plot is for which angle because, for the purposes of this discussion, it doesn’t matter. I’m only interested in talking about how different the loudspeaker sounds at different angles – not the specifics of how it sounds different.

The third plot shows the total phase response of the system, at a position that is on axis to the loudspeaker (and therefore equidistant to both drivers). As you can see there, a perfect 2-way loudspeaker with a 4th order Linkwitz-Riley crossover behaves as a 4th-order allpass filter. In other words, at low frequencies, the output is in phase with the input. At the crossover frequency, the output is 180° out of phase with the input. At high frequencies, the output is 360° out of phase with the input.

The fourth plot shows the step response of the total system, at a position that is on axis to the loudspeaker (and therefore equidistant to both drivers). As you can see there, a perfect 2-way loudspeaker with a 4th order Linkwitz-Riley crossover does not give you a “perfect” step response – it can’t, since it acts an allpass filter. The weird shape you see there is cause by the fact that the high frequencies are not “in phase” with the low frequencies. (I know, I know… different frequencies cannot be “in phase”.) Since different frequencies are delayed differently by the total system, they do not add up correctly in the time domain. Thus, although the total output in terms of magnitude is flat (hence the flat on-axis frrequency response) the time response will be weird.

Looking in detail at the step response plot, you can see that it takes about 1.5 ms for the total output to settle to a value of 1. The actual time that it takes is dependent on the crossover frequency. The lower the frequency, the longer it will take. It’s the shape of the step response that’s determined by the crossover’s phase response. What can be seen from the shape is that the high-frequency spike hits first (as we would expect), then the step response drops back to a negative value before heading upwards. It overshoots, peaking at a value of 1.0558 before coming back down, undershooting slightly (to a value of 0.9976)  and finally settling at a value of 1. Note that these values won’t change with changes in crossover frequency – they’ll just happen at a different time. The higher the frequency, the faster the response.

Whether or not this modified time response is worth worrying about (i.e. can you hear it) is also outside of the scope of today’s discussion. All we’re going to say for today is that this temporal distortion exists, and it is different for different crossover strategies as we’ll see below.

Linkwitz-Riley 2nd Order

A second possible crossover strategy is to use a 2nd-order Linkwitz Riley. This is similar to a 4th-order, except that instead of putting two 12 dB/octave Butterworth filters in series to make each section, you put two 6 dB/octave Butterworth filters in series.

Since the total filters applied to make the high pass and low pass sections of this crossover are each made with only two first-order filters (instead of two second-order filters), the high pass and low pass sections are only 180 degrees out of phase with each other (at all frequencies). Consequently, in order to get them to add back together without cancelling completely at the crossover frequency, you have to invert the polarity of one of the sections. (We’ll do this to the high pass section, just in case you can hear your woofers pulling when they ought to push when a kick drum hits). On the plus side, since they’re 180 degrees out of phase at all frequencies, if you DO flip the polarity of your high pass section, they’ll add back together (on axis) to give you a flat magnitude response.

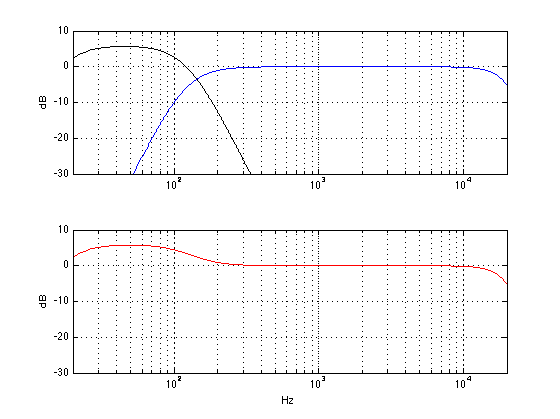
As you can see in the above plots, the slopes of the high pass and low pass sections in this crossover type are more gentle than in the 4th order Linkwitz Riley. This should be obvious, since they have a lower order. In the second plot, you can see that, on-axis, the magnitude response is flat, just as we would expect. However, there are implications on the off-axis response. The deviation from “flat” is greater with the 2nd-order LR than it is with the 4th-order version. Not by much, admittedly, but it is greater. So, if you’re concerned about deviations in your off-axis response in the vertical plane, you might prefer the 4th-order LR over the 2nd-order variant.

If, however, you lay awake at night worring about phase response (you know who you are – yes – I’m talking you YOU) then you might prefer the 2nd-order Linkwitz Riley, since, as you can see in the third plot, the total output is only 180° out of phase with its input in the worst case – only half that of the 4th-order variant. On the other hand, since it’s 180° out of phase, that means that a high voltage going into the system (at high frequencies) will come out as a low pressure. So, if you’re the kind of person who lays awake at night worrying about “absolute phase” (you know who you are – yes – I’m talking to YOU) then this might not be your first choice.

Finally, take a look at the step response in the final plot. You’ll notice immediately that the high frequencies are 180° out iof phase, since the initial transient of the step goes down instead of up. You’ll also notice that the step “recovers” to a value of 1 a little faster than the 4th order Linkwitz Riley. Note that, a 2nd order LR, doesn’t have the overshoot that we saw in the 4th order version.

Butterworth, 12 db/octave

Possibly the most common passive crossover type (and therefore, possibly the most common crossover  type, period!) is the 12 dB/octave Butterworth crossover. This is made by using a 2nd-order Butterworth filter for each section (the high pass and the low pass).

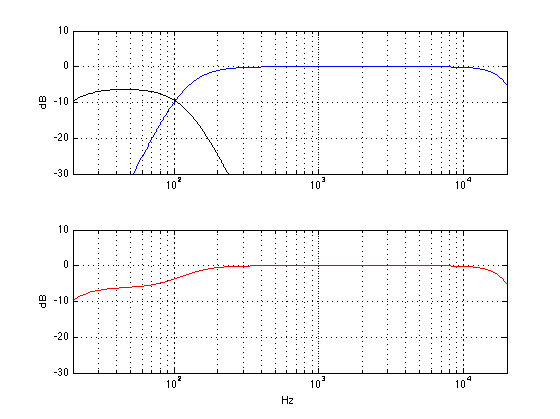
You’ll notice in the top plot that this means that the filter sections are only 3 dB down at the crossover frequency. This has some implications on the on-axis response. Since the two filter sections are 180° out of phase with each other (at all frequencies – just like the 2nd-order LR crossover) then we have to flip the polarity of one of the sections (the high-pass section again, for all the same reasons) to prevent them from cancelling each other at the crossover frequency when they’re added back together. However, now we have a problem. Since the two sections are in-phase (due to the 180° phase shift plus the polarity flip) and since they’re only 3 dB down at the crossover frequency, when they get added back together, you get more out than you put into the system. This can be seen in the second plot, where the total magnitude response has a bump at the crossover frequency – even when on-axis.

Of course, a 3 dB bump in the magnitude response will be audible, at the very least as a change in timbre (3 dB is, after all, twice the power). We can also see that there is a small, but visible change in the overall magnitude response as you change the vertical angle to the listener.

The third plot shows that a 12 dB/Octave Butterworth crossover, when all other issues are ignored, acts as a 2nd-order allpass filter with a worst-case phase distortion of 180°.

Finally, the fourth plot shows that its step response is similar, but not identical to, the 2nd-order LR crossover. The initial transient goes negative because we have inverted the polarity of the high pass section. Unlike the 2nd-order LR (but similar to the 4th-order LR), however, there is an overshoot and undershoot before the response settles at a value of 1. That overshoot reaches a maximum of 1.1340, and the subsequent undershoot goes down to 0.9942.

Butterworth, 18 db/oct

Constant Voltage, (using a Butterworth, 18 db/oct high pass)

There is a group of persons who believe that the step response (or the shape of a square wave through the system) is the be-all-and-end-all for determining the quality of a system. The logic goes that, if a square wave goes in, and a square wave comes out, then the system is perfect. This is true – if you mean “perfect at reproducing square waves” – which may or may not be important.

Following this logic, the idea is that, if you take your initial input and make a filtered version, then all you need to do is to subtract that filtered version from the input to get the remainder. If you then add the remainder and the filtered section, you get out what you put in, so the system is perfect. At least, that’s the idea. Let’s see how well that works out, shall we?

(By the way, the name for this classification of crossovers is “constant voltage” crossovers, and there are lots of different ways to implement them. Richard Small wrote some good stuff about them in some AES papers once-upon-a-time, if you’re curious.)

So, let’s look at one fairly-common implementation of a constant voltage crossover. We’ll take the input, filter it with an 18 dB / Octave Butterworth filter and use that for the high pass section. The low pass section is created by subtracting the high pass section from the input, and we just take what we get.

As you can see in the top plot, the result of this is that the low pass section is a little weird. It has a rather large bump in its magnitude response around the crossover frequency. In addition, the slope of the high pass roll-off is not very steep. This all might be okay, if your lower driver is able to handle it, but it might not. (Note that, if we had made a Butterworth low pass and used the subtraction trick to get the high pass section, the bump would have appeared in the high pass section, which would result in too much low-frequency energy in the tweeter, thus likely making it unhappy… That’s why we used a Butterworth high pass to start.)

Let’s skip the next plot and look at the third and fourth. As you can see in both of these, the constant voltage crossover is unique in that it has no phase distortion, and the step response is perfect. This is to be expected, since these are the primary criteria behind the design of this type of crossover.

Now, let’s look at the second plot. As you can see there, the off-axis response of a constant voltage crossover is a complete disaster. So, if you’re the kind of person who thinks that off-axis response is important – or at least worth considering, you should probably stay away from this crossover. However, if you have an acoustically absorptive floor and an acoustically absorptive ceiling (so no vertical reflections) and you never stand up, and you’re inside the room’s critical distance with respect to the loudspeaker, then this little problem might not be an issue for you.

Concluding comments

The thing that you have to remember for all of the stuff I’ve said here is that it’s only applicable within the limitations of the parameters I stated at the beginning. If your drivers are imperfect, or if you have a high pass in series with your low pass section because your loudspeaker driver exists in real life (it does), or if you have a symmetrical driver arrangement (sometimes called a D’Appolito design, named after the first person to be smart enough to publish a paper about it), then all of these results will be different.

Also, the other important thing to remember is that I’m making no claims about whether these “problems” are audible. They might be – and they might not be. But don’t just jump to conclusions all willy-nilly and assume that, because you can see a difference in these plots, you’ll be able to hear the difference in your loudspeakers. Then again, that doesn’t mean that I’m saying “you can’t!” What I’m saying is “I don’t know whether you can hear these issues or not – any of them.”

P.S .

Happy New Year.