Category: headphones

Acoustic measurements: Part 3

In Part 2, I showed the raw magnitude response results of three pairs of headphones measured on three different systems, each done 5 times. However, when you plot magnitude responses on a scale with 80 dB like I did there, it’s difficult to see what’s going on.

Differences in measurements relative to average

One way to get around this issue is to ignore the raw measurement and look at the differences between them, which is what we’ll do here. This allows us to “zoom in” on the variations in the measurements, at the cost of knowing what the general overall responses are.

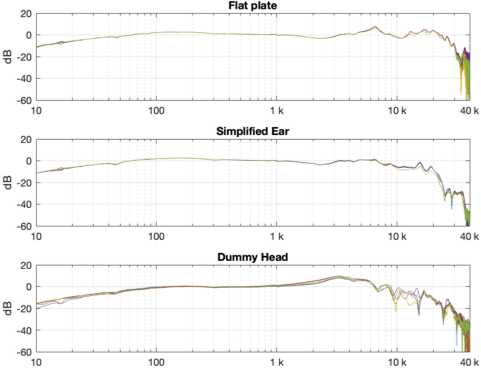
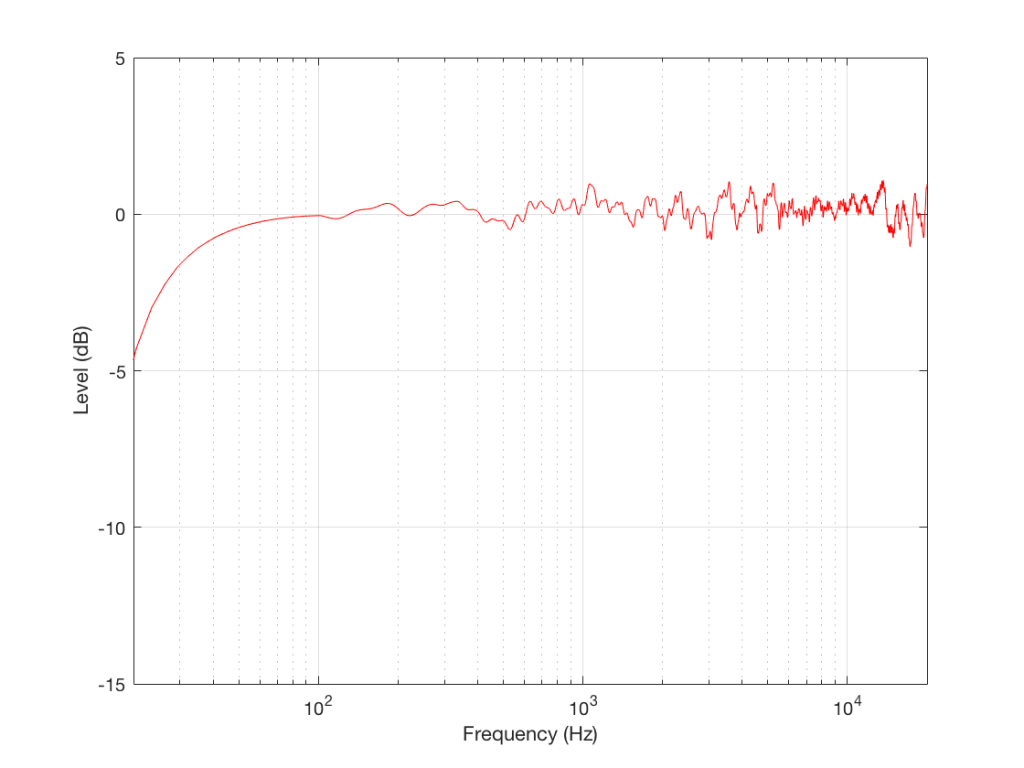
Figure 1 in Part 2 showed the 5 x 3 sets of raw magnitude responses of the open headphones. I then take each set of 5 measurements (remember that these 5 measurements were done by removing the headphones and re-setting them each time on the measurement rig) and find their average response. Then I plot the difference between each of the 5 measurements and that average, and this is done for each of the three measurement systems, as shown below in Figure 1.

Figure 1: Open headphones: The difference between each of the 5 measurements done on each system and the mean (average) of those 5 measurements.
Figure 2: Semi-open headphones: The difference between each of the 5 measurements done on each system and the mean (average) of those 5 measurements.
Figure 3: Closed headphones: The difference between each of the 5 measurements done on each system and the mean (average) of those 5 measurements.

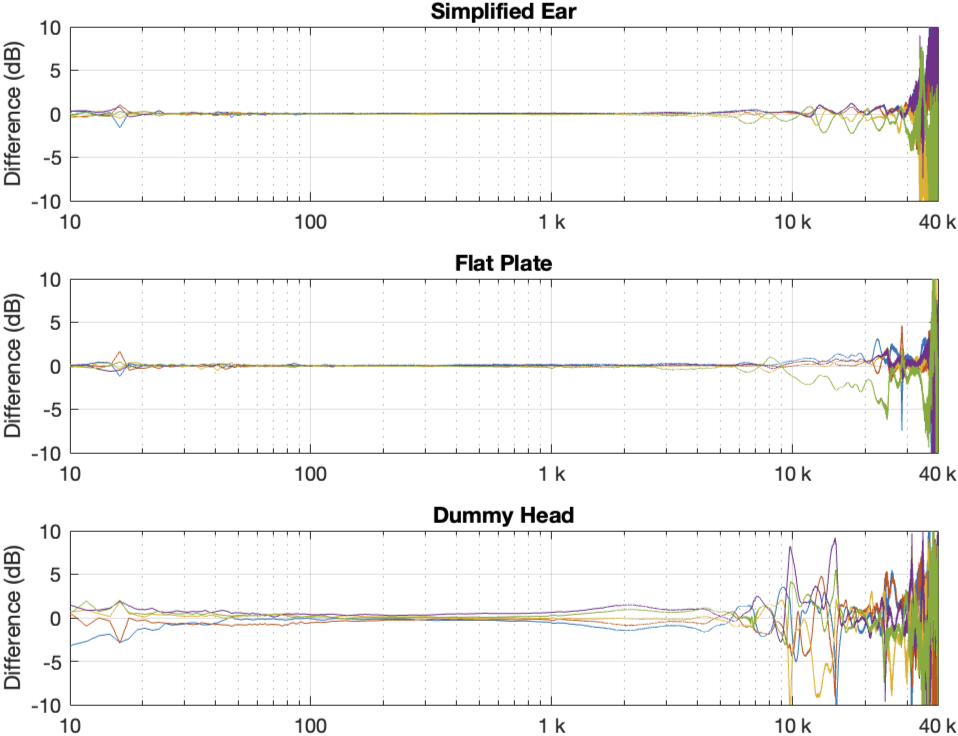
Some of the things that were intuitively visible in the plots in Part 2 are now obvious:

  • There is a huge change in the measured magnitude response in the high frequency bands, even when the pair of headphones and the measurement rig are the same. This is the result of small changes in the physical position of the headphones on the rig, as well as changes in the clamping force (modified by moving the headband extension). I intentionally made both of these “errors” to show the problem. Notice that the differences here are greater than ±10 dB, which is a LOT.
  • Overall, the differences between the measurements on the dummy head are bigger and have a lower frequency range than for the other two systems. This is mostly due to two things:
    • because the dummy head has pinnae (ears), very small changes in position result in big changes in response
    • it is easier to have small leaks around the ear cushions on a dummy head than with a flat surrounding of a metal plate or an artificial ear. This is the reason for the low-frequency differences with the closed headphones. Leaks have no effect on open headphone designs, since they are always leaking out through the diaphragm itself.

The differences that you can see here are the reason that, when we’re measuring headphones, we never measure just once. We always do a minimum of 5 measurements and look at the average of the set. This is standard practice, both for headphone developers and experienced reviewers like this one, for example.

In addition to this averaging, it’s also smart to do some kind of smoothing (which I have not done here…) to avoid being distracted by sharp changes in the response. Sharp peaks and dips can be a problem, particularly when you look at the phase response, the group delay, or looking for ringing in the time domain. However, it’s important to remember that the peaks and dips that you see in the measurements above might not actually be there when you put the headphones on your head. For example, if the variations are caused by standing waves inside the headphones due to the fact that the measurement system itself is made of reflective plastic or metal (but remember that you aren’t…) then the measurement is correct, but it doesn’t reflect (ha ha…) reality…

One additional thing to remember with these plots is that something that looks like a peak in the curve MIGHT be a peak, but it might also be a dip in the average curve because we’re only looking at the differences in the responses.

System differences

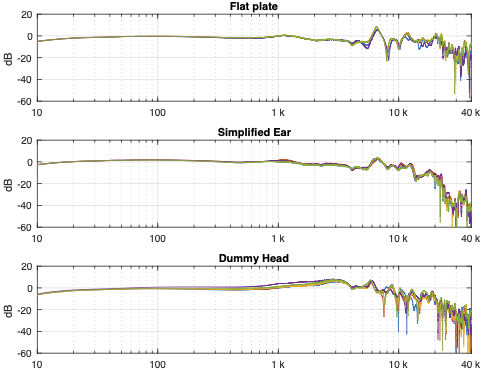
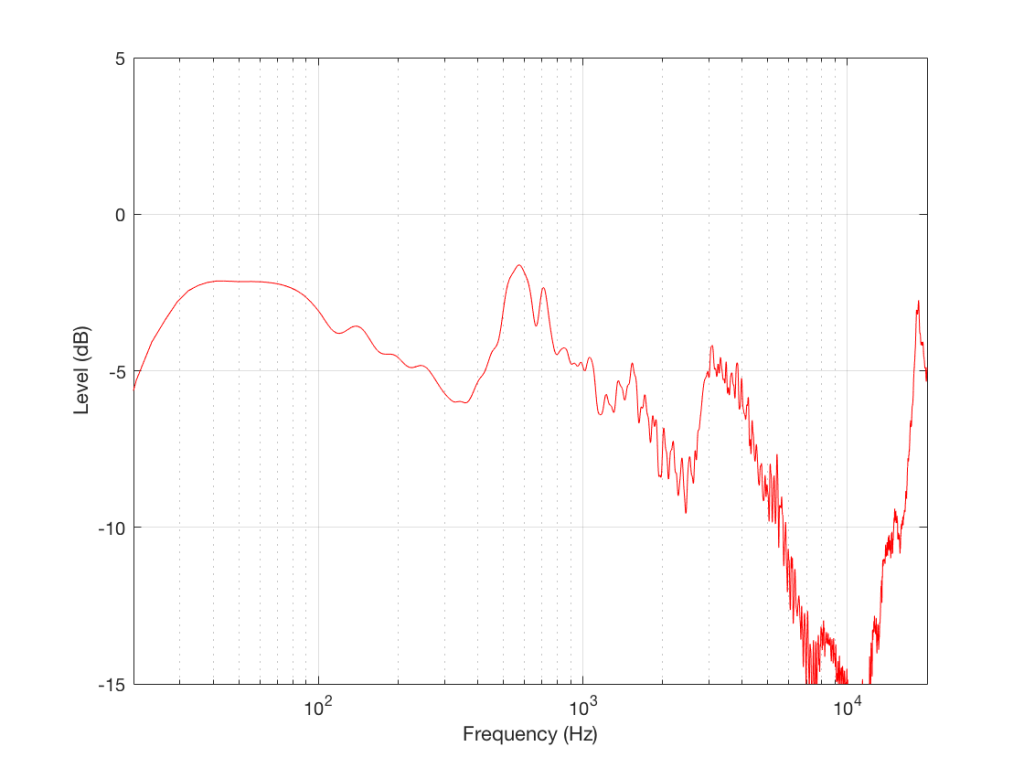
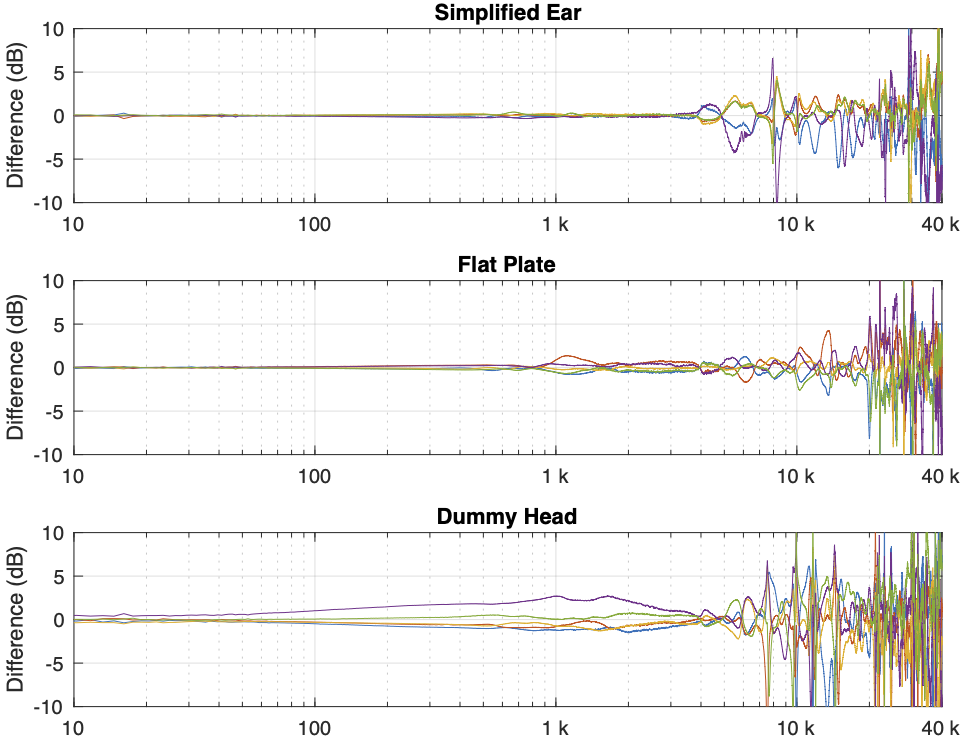
Instead of looking at the differences between each individual measurement and the average of the measurement set, we can also look at the differences between what each measurement system is telling us for each headphone type. For example, if I take one measurement of a pair of headphones on each system, and pretend that one of them is “correct”, then I can find the difference between the measurements from the other two systems and that “reference”.

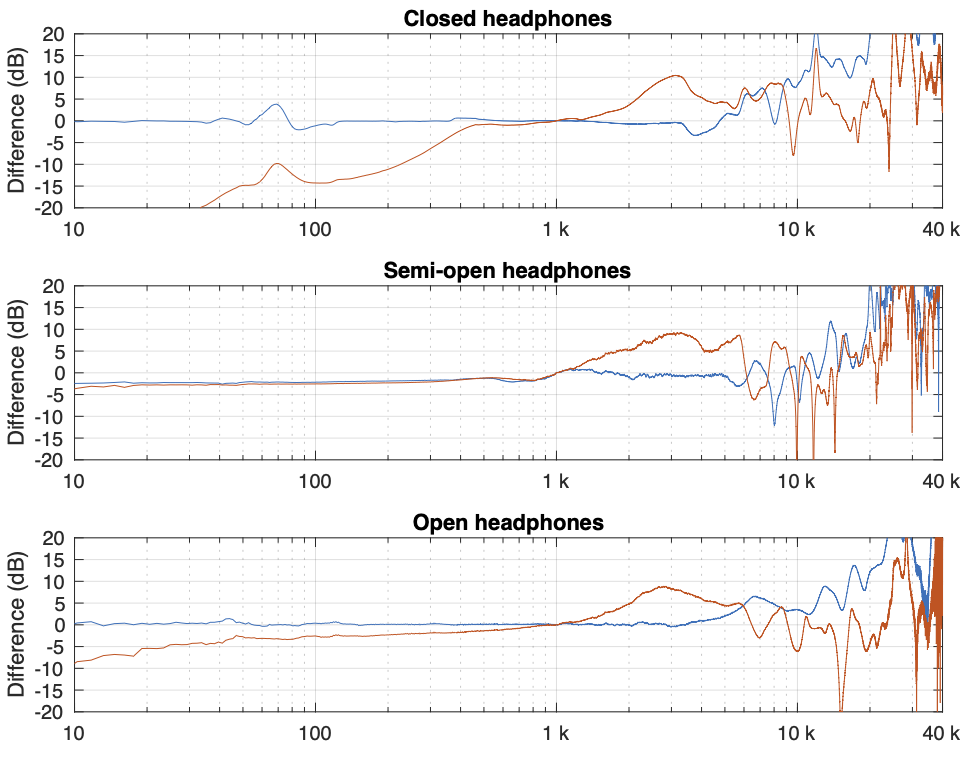
Figure 4. One measurement for each pair of headphones on each measurement system. The red curves are the dummy head and the blue curves are the artificial ear RELATIVE TO THE FLAT PLATE.

In Figure 4, I’m pretending that the flat plate is the “correct” system, and then I’m plotting the difference between the dummy head measurement (in red) and the artificial ear measurement (in blue) relative to it.

Again, it’s important to remember with these plots is that something that looks like a peak in the curve might actually be a dip in the “reference” curve. (The bump in the red lines around 2 – 3 kHz is an example of this…)

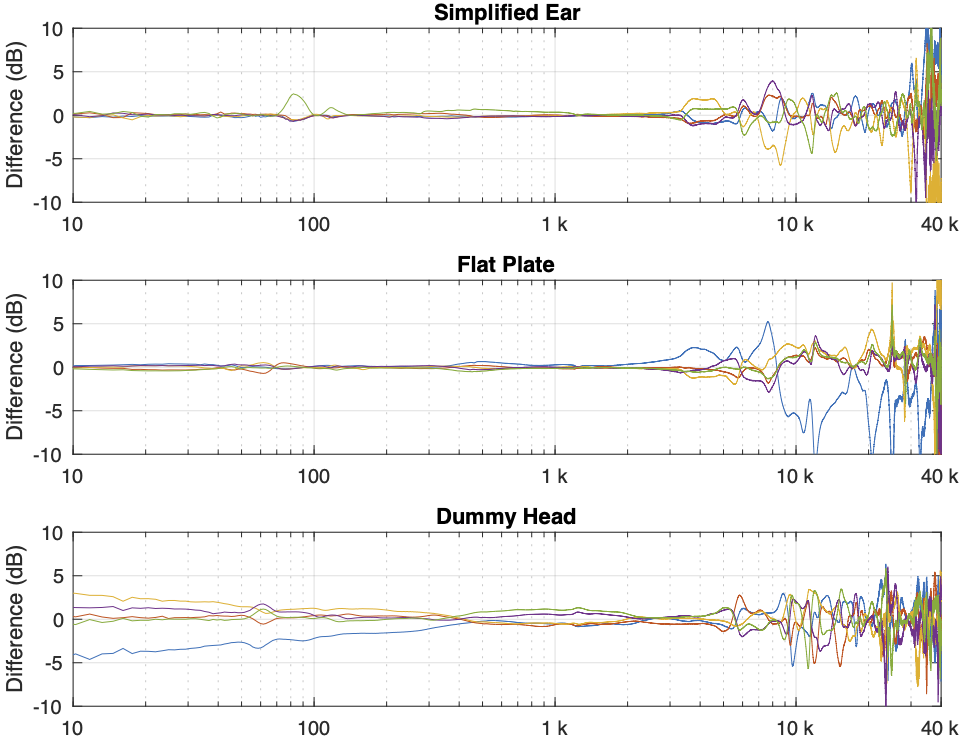
Of course, you could say “but you just said that we shouldn’t look at a single measurement”… which is correct. If we use the averages of all 5 measurements for each set and do the same plot, the result is Figure 5.

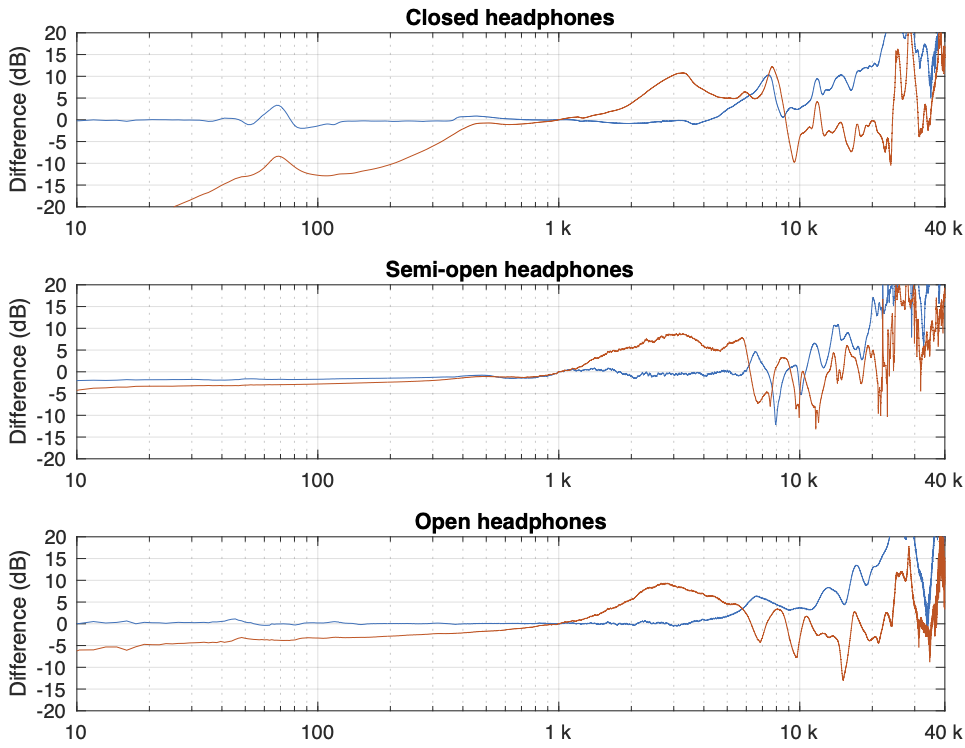
Figure 5. The average of all 5 measurements for each pair of headphones on each measurement system. The red curves are the dummy head and the blue curves are the artificial ear relative to the flat plate.

You can see there that, by using the averaged responses instead of individual measurements, the really sharp peaks and dips disappear, since they smooth each other out.

Comparing headphone types

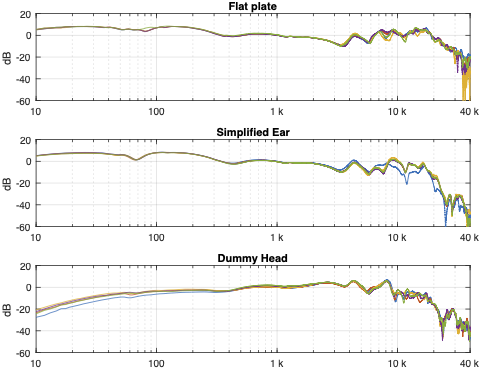
Things get even more complicated if you try to compare the headphones to each other using the measurement systems. Figure 6, below, shows the averages of the five measurements of each pair of headphones on each measurement system, plotted together on the same graphs (normalised to the levels at 1 kHz), one for each measurement system.

Figure 6: Comparing the three pairs of headphones on each measurement system.

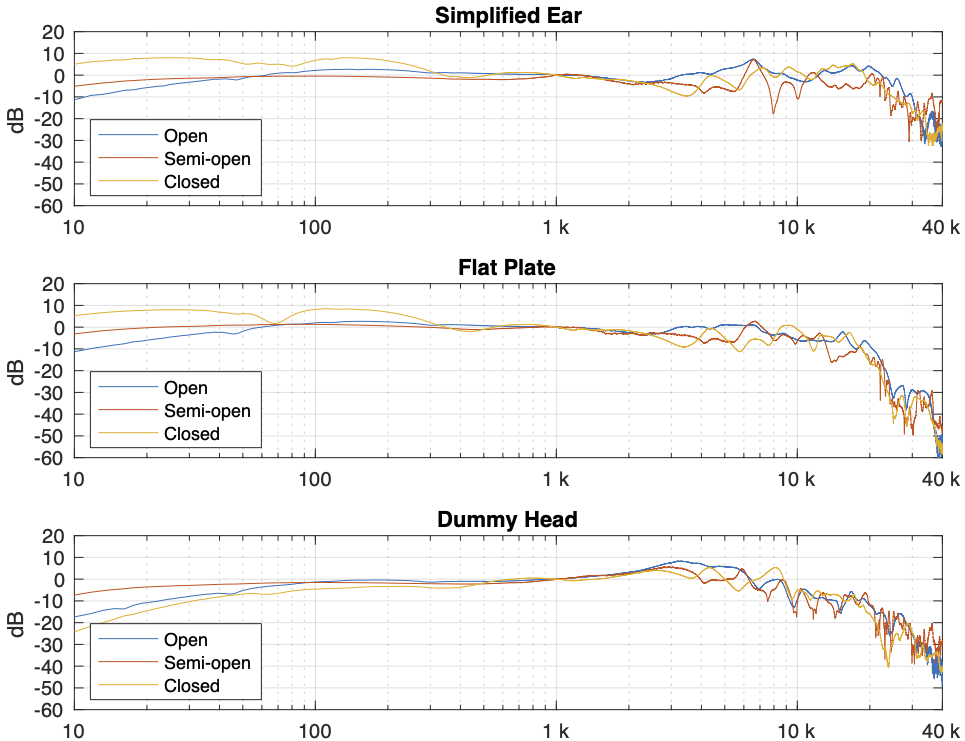
This is actually a really important figure, since it shows that the same headphones measured the same way on different systems tell you very different things. For example, if you use the “simplified ear” or the “flat plate” system, you’ll believe that the closed headphones (the yellow line) is about 10 – 15 dB higher than the open headphones (the blue line) in the low frequency region. However, if you use the “dummy head” system, you’ll believe that the closed headphones (the yellow line) is about 5 – 10 dB lower than the open headphones (the blue line) in the low frequency region.

Which one is correct? They all are, even though they tell you different things. After all, it’s just data… The reason this happens is that one measurement system cannot be used to directly compare two different types of headphones because their acoustic impedances are different. With experience, you can learn to interpret the data you’re shown to get some idea of what’s going on. However, “experience” in that sentence means “years of correlating how the headphones sound with how the plots look with the measurement system(s) you use”. If you aren’t familiar with the measurement system and how it filters the measurement, then you won’t be able to interpret the data you get from it.

That said, you MIGHT be able to use one system to compare two different pairs of open headphones or two different pairs of closed headphones, but you can’t directly compare measurements of different headphone types (e.g. open and closed) reliably.

This also means that, if you subscribe to two different headphone magazines both of which use measurements as part of their reviews, and one of them uses a flat plate system while the other uses a dummy head, the same pairs of headphones might get opposite reviews in the two magazines…

Which review can you trust? Both of them – and neither of them.

Conclusions

Looking at these plots, you could come to the conclusion that you can’t trust anything, because no two measurements tell you the same things about the same devices. This is the incorrect conclusion to draw. These measurement systems are tools that we use to tell us something about the headphones on which we’re working. And people who use these tools daily know how to interpret the data they see from them. If something looks weird, they either expected it to look weird, or they run the measurement on another system to get a different view.

The danger comes when you make one measurement on one device and hold that up as The Truth. A result that you get from any one of these systems is not The Truth, but it is A Truth – you just need more information. If you’re only shown one measurement (or even an average of measurements) that was done on only one measurement system, then you should raise at least one eyebrow, and ask some questions about how that choice of system affects the plots that you see.

In many ways, it’s like looking at a recipe in a cookbook. You might be able to determine whether you might like or probably hate a dish by reading its description of ingredients and how to prepare it. But you cannot know how it’ll taste until you make it and put it in your mouth. And, if you cook like I do, it’ll be just a little different next time. It’s cooking – not a chemistry experiment. If you use headphones like I do, it’ll also be a little different next time because some days, I don’t wear my glasses, or I position the head band a little differently, so the leak around the ear cushion or the clamping force is a little different.

Acoustic measurements: Part 2

In Part 1, I talked about how any measurement of an audio device tells you something about how it behaves, but you need to know a LOT more than what you can learn from one measurements. This is especially true for a loudspeaker where you have the extra dimensions of physical space to consider.

Thought experiment: Fridges vs. Mosquitos

Consider a situation where you’re sitting at your kitchen table, and you can hear the compressor in your fridge humming/buzzing over on the other side of the room. If you make a small movement in your chair, the hum from the fridge sounds the same to you. This is partly because the distance from the fridge to you is much bigger than the changes in that distance that result from you shifting your butt.

Now think about the times you’ve been trying to sleep on a summer night, and there’s a mosquito that is flying near your ear. Very small changes in the location of that mosquito result in VERY big changes in how it sounds to you. This is because, relative to the distance to the mosquito, the changes in distance are big.

In other words, in the case of the fridge (that’s say, 3 m away) by moving 10 cm in your chair, you were changing the distance by about 3%, but the mosquito was changing its distance by more than 100% by moving just from 1 cm to 2 cm away.

In other words, a small change in distance makes a big change in sound when the distance is small to begin with.

The challenges of measuring headphones

The methods we use for measuring the magnitude response of a pair of headphones is similar to that used for measuring a loudspeaker. We send a measurement signal to the headphones from a computer, that signal comes out and is received by a microphone that sends its output back to the computer. The computer then is used to determine the difference between what it sent out and what came back. Simple, right?

Wrong.

The problems start with the fact that there are some fundamental differences between headphones and loudspeakers. For starters, there’s no “listening room” with headphones, so we don’t put a microphone 3 m away from the headphones: that wouldn’t make any sense. Instead, we put the headphones on some kind of a device that either simulates an ear, or a head, or a head with ears (with or without ear canals), and that device has a microphone (roughly) where your eardrum would be. Simple, right?

Wrong.

The problem in that sentence was the word “simulates”. How do you simulate an ear or a head or a head with ears? My ears are not shaped identically to yours or anyone else’s. My head is a different size than yours. I don’t have any hair, but you might. I wear glasses, but you might not. There are many things that make us different physically, so how can the device that we use to measure the headphones “simulate” us all? The simple answer to this question is “it can’t.”

This problem is compounded with the fact that measurement devices are usually made out of plastic and metal instead of human skin, so the headphones themselves “see” a different “acoustic load” on the measurement device than they do when they’re on a human head. (The people I work with call this your acoustic impedance.)

However, if your day job is to develop or test headphones, you need to use something to measure how they’re behaving. So, we do.

Headphone measurement systems

There are three basic types of devices that are used to measure headphones.

  • an artificial ear is typically a metal plate with a depression in the middle. At the bottom of the depression is a microphone. In theory, the acoustic impedance of this is similar to a human ear/pinna + the surrounding part of your head. In practice, this is impossible.
  • a headphone test fixture looks like a big metal can lying on its side (about the size of an old coffee can, for example) on a base. It might have flat metal sides, or it could have rubber pinnae (the fancy word for ears) mounted on it instead. In the centre of each circular end is a microphone.
  • a dummy head looks like a simplified model of a human head (typically a man’s head). It might have pinnae, but it might not. If it does, those pinnae might look very much like human ears, or they could look like simplified versions instead. There are microphones where you would expect them, and they might be at the bottom of ear canals, but you can also get dummy heads without ear canals where the microphones are flush with the side of the head.

The test system you use is up to you – but you have to know that they will all tell you something different. This is not only because each of them has a different acoustic response, but also because their different shapes and materials make the headphones themselves behave differently.

That last sentence is important to remember, not just for headphone measurement systems but also for you. If your head and my head are different from each other, AND your pinnae and my pinnae are different from each other, THEN, if I lend you my headphones, the headphones themselves will behave differently on your head than they do on my head. It’s not just our opinions of how they sound that are different – they actually sound different at our two sets of eardrums.

General headphone types

If I oversimplify headphone design, we can talk about two basic acoustical type of headphones: They can be closed (where the back of the diaphragm is enclosed in a sealed cabinet, and so the outside of the headphones is typically made of metal or plastic) or open (where the back of the diaphragm is exposed to the outside world, typically through a metal screen). I’d say that some kinds of headphones can be called semi-open, which just means that the screen has smaller (and/or fewer) holes in it, so there’s less acoustical “transparency” to the outside world.

Examples

To show that all these combinations are different, I took three pairs of headphones

  • open headphones
  • semi-open headphones
  • closed headphones

and I measured each of them on three test devices

  • artificial “simplified” ear
  • text fixture with a flat-plate
  • dummy head

In addition, to illustrate an additional issue (the “mosquito problem”), I did each of these 9 measurements 5 times, removing and replacing the headphones between each measurement. I was intentionally sloppy when placing the headphones on the devices, but kept my accuracy within ±5 mm of the “correct” location. I also changed the clamping force of the headphones on the test devices (by changing the extension of the headband to a random place each time) since this also has a measurable effect on the measured response.

Do not bother asking which headphones I measured or which test systems I used. I’m not telling, since it doesn’t matter. Not to me, anyway…

The raw results

I did these measurements using a 10-second sinusoidal sweep from 2 Hz to Nyquist, on a system running at 96 kHz. I’m plotting the magnitude responses with a range from 10 Hz to 40 kHz. However, since the sweep starts at 2 Hz, you can’t really trust the results below 20 Hz (a decade below the lowest frequency of interest is a good rule of thumb when using sine sweeps).

Figure 1: The “raw” magnitude responses of the open headphones measured 5 times each on the three systems
Figure 2: The “raw” magnitude responses of the semi-open headphones measured 5 times each on the three systems
Figure 3: The “raw” magnitude responses of the closed headphones measured 5 times each on the three systems

Looking at the results in the plots above, you can come to some very quick conclusions:

  • All of the measurements are different from each other, even when you’re looking at the same headphones on the same measurement device. This is especially true in the high frequency bands.
  • Each pair of headphones looks like it has a different response on each measurement system.
    For example, looking at Figure 3, the response of the headphones looks different when measured on a flat plate than on a dummy head.
  • The difference in the results of the systems are different with the different headphone types.
    For example, the three sets of plots for the “semi-open” headphones (Fig. 2) look more similar to each other than the three sets of plots for the “closed” headphones (Fig. 3)
  • the scale of these differences is big. Notice that we have an 80 dB scale on all plots… We’re not dealing with subtleties here…

In Part 3 of this series, we’ll dig into those raw results a little to compare and contrast them and talk a little about why they are as different as they are.

Acoustic measurements: Part 1

People who work in the audio industry use all kinds of different measurements to evaluate the performance of equipment. In many cases, the measurements we do are chosen because they’re easy to do (or because they were easy to do in “The Old Days”), and not because they accurately represent how the equipment actually behaves.

Magnitude response

One simple example of this is what most people call a frequency response but what is actually a magnitude response. This is a measure of how the level of an audio signal is changed by the device under test (the “DUT”) as a function of frequency. For example, if you’re measuring a RIAA-spec preamplifier (used for converting a turntable’s pickup’s output to a “line” level signal), then it should have a magnitude response that looks like the red line in the plot in Figure 1.

Figure 1: The red line shows the correct magnitude response for the frequency-dependent filtering in a RIAA phono preamplifier.

This curve shows that, relative to a signal at 1 kHz, the lower the frequency, the more gain is applied to the signal and the higher the frequency, the more attenuation is applied to the signal. Note that this curve is normalised to the level at 1 kHz, which should actually be +40 dB higher if we were to include the frequency-independent gain of the system.

It’s important to remember that this plot shows us only one thing: the change in level caused by the DUT as a function of a change in frequency of the signal. What this plot does NOT show us is much, much more… For example:

  • We don’t know anything about the behaviour of the system outside the boundaries of this plot.
  • We don’t know anything about its phase response.
  • We don’t know anything about how loud the noise of the DUT is.
  • We don’t know if this plot is true if we were to measure the DUT at a different input level.
  • We don’t know whether the DUT would have a different behaviour if the device that was feeding it had a different output impedance.
  • We don’t know whether the DUT would have a different behaviour if the device that it was feeding had a different input impedance.
  • We don’t know anything about whether the signal has any non-linear distortion artefacts.
    (Notice that I didn’t say “…whether the signal is distorted” because we know it’s distorted, since the output of the DUT is not the same as the input of the DUT. Any change in the signal is a form of distortion of the signal.)

I’m not saying that a simple magnitude response plot of a DUT is not useful. I’m just saying that it’s not enough information. It’s like asking for the temperature of a cup of coffee. It’s useful information, but it doesn’t tell you enough to know whether you’re going to enjoy drinking it (unless, of course, you hate coffee…)

This problem gets even worse when you’re measuring the acoustic output of a device like a loudspeaker or a pair of headphones, for example. (The acoustic input of a microphone is a similar problem in the opposite direction.)

Let’s start by thinking about a loudspeaker’s output in real life.

  1. You have a device that radiates sound in space in all directions. Let’s look at that space from the loudspeaker’s perspective and say that this means an angle of rotation around the loudspeaker, and an angle of elevation above/below the loudspeaker. That makes two dimensions.
  2. If we’re talking about the loudspeaker’s magnitude response, then we’re looking at its output level (one dimension) as a function of frequency (one more dimension).
  3. That speaker is (usually) in a room, and you’re probably also there too. We can then that this is in three-dimensional space when we talk about the walls, floor, ceiling, and your location inside that space.
  4. Since the surfaces in the room reflect the audio signal, then the time at which the signal arrives at the listening position must also be considered. The “sound” of a loudspeaker at a listening position before the first reflection arrives is different than after a bunch of reflections are coming in and the room has started resonating as well. So, time adds one more dimension to the problem.
  5. We’ll ignore the non-linear distortion artefacts produced by the loudspeaker and the fact that they radiate in different directions differently, since it’s already complicated enough… However, if we were to add things like changes in the response due to temperature of the voice coil or directionally-dependent distortion artefacts like breakup, this would wind up being a much longer discussion…

So, just looking at the small list of “usual suspects” above, we can see that evaluating the sound of a single loudspeaker in a listening room is at least an 8-dimensional problem. And this doesn’t even take things like 2-channel stereo or 7.1.4 multichannel or whether you’re listening to Aretha Franklin or Stockhausen into account…

In other words, it’s complicated. So, we use reductionism to try to start to get an idea of what’s going on. We put a microphone directly in front of a loudspeaker and measure its magnitude response at one level using one kind of test signal (e.g. a swept sine wave or an MLS) and we remove all the room’s reflections somehow. This reduces our 8-dimensional problem to a 2-dimensional version: we have level as a function of frequency and nothing else, since we’ve chosen to throw away everything else by the way we did the measurement.

Figure 2: The on-axis, free-field magnitude response of a loudspeaker.

For example, take a look at the magnitude response shown in Figure 2, which is a real measurement of a real loudspeaker. This measurement was performed using a swept-sine (a sinusoidal wave with a frequency that changes smoothly over time, typically from low to high) with a microphone on-axis to the loudspeaker at a distance of 3 m. The measurement was time-windowed to remove the room reflections, and therefore can be considered to be a “free field” (a sound field that is free of reflections) measurement. However, the roll-off in the low end is actually a combination of the actual response of the loudspeaker and the artefacts of using a shorter time window. (We would have needed to use a much bigger room to get less influence from the time windowing.)

So, this plot ONLY tells us how the loudspeaker behaves at one point in infinite space, when we’re ONLY asking “how does the level of the loudspeaker’s output vary with changes in frequency and we ONLY play sinusoidal signals at one level.” This is all useful information, but we need to know more – otherwise, we’ll jump to conclusions about whether this loudspeaker sounds “good” or not.

Just like looking at ONLY the temperature of a cup of coffee, this doesn’t give us enough of the story to know how the loudspeaker will “sound” (no matter what a magazine reviewer will try and tell you…).

In other words, if we use reductionism to understand the problem, you simplify the question so much that the problem you wind up understanding is not the same as the thing you’re trying to understand in the first place.

For example, if we measure that same loudspeaker at a different angle (by rotating the loudspeaker and leaving the microphone in place) we’ll see a magnitude response like the one shown in Figure 3.

Figure 3: The free-field magnitude response of the same loudspeaker, measured at 90º off-axis.

This magnitude response is the output of the same loudspeaker at 90º off-axis, which might be what’s heading towards your side-wall. If your side wall is perfectly reflective, then this is therefore the magnitude response of your first reflection, which might be a bad thing if you think that it’s important.

So, when you’re looking at any one measurement of anything, you don’t have enough information to know enough to make a general evaluation. However, unfortunately, many people will run with this information and make the evaluation anyway. It’s data, and data doesn’t lie, so this tells the truth, right?

Wrong. Because it’s only a portion of the total truth.

For example, you can say that “organic food is good for me” but I have an allergy to peanuts. So if I eat organic peanuts, I have about 20 minutes to get to a hospital. Much longer than that and I need a funeral home instead. “Organic” is true, but not enough information for me to know whether or not it’ll be an uneventful meal.

What is a “virtual” loudspeaker? Part 3

#91.3 in a series of articles about the technology behind Bang & Olufsen

In Part 1 of this series, I talked about how a binaural audio signal can (hypothetically, with HRTFs that match your personal ones) be used to simulate the sound of a source (like a loudspeaker, for example) in space. However, to work, you have to make sure that the left and right ears get completely isolated signals (using earphones, for example).

In Part 2, I showed how, with enough processing power, a large amount of luck (using HRTFs that match your personal ones PLUS the promise that you’re in exactly the correct location), and a room that has no walls, floor or ceiling, you can get a pair of loudspeakers to behave like a pair of headphones using crosstalk cancellation.

There’s not much left to do to create a virtual loudspeaker. All we need to do is to:

  • Take the signal that should be sent to a right surround loudspeaker (for example) and filter it using the HRTFs that correspond to a sound source in the location that this loudspeaker would be in. REMEMBER that this signal has to get to your two ears since you would have used your two ears to hear an actual loudspeaker in that location.
  • Send those two signals through a crosstalk cancellation processing system that causes your two loudspeakers to behave more like a pair of headphones.
Figure 1: A block diagram of the system described above.

One nice thing about this system is that the crosstalk cancellation is only there to ensure that the actual loudspeakers behave more like headphones. So, if you want to create more virtual channels, you don’t need to duplicate the crosstalk cancellation processor. You only need to create the binaurally-processed versions of each input signal and mix those together before sending the total result to the crosstalk cancellation processor, as shown below.

Figure 2: You only need one crosstalk cancellation system for any number of virtual channels.

This is good because it saves on processing power.

So, there are some important things to realise after having read this series:

  • All “virtual” loudspeakers’ signals are actually produced by the left and right loudspeakers in the system. In the case of the Beosound Theatre, these are the Left and Right Front-firing outputs.
  • Any single virtual loudspeaker (for example, the Left Surround) requires BOTH output channels to produce sound.
  • If the delays (aka Speaker Distance) and gains (aka Speaker Levels) of the REAL outputs are incorrect at the listening position, then the crosstalk cancellation will not work and the virtual loudspeaker simulation system won’t work. How badly is doesn’t work depends on how wrong the delays and gains are.
  • The virtual loudspeaker effect will be experienced differently by different persons because it’s depending on how closely your actual personal HRTFs match those predicted in the processor. So, don’t get into fights with your friends on the sofa about where you hear the helicopter…
  • The listening room’s acoustical behaviour will also have an effect on the crosstalk cancellation. For example, strong early reflections will “infect” the signals at the listening position and may/will cause the cancellation to not work as well. So, the results will vary not only with changes in rooms but also speaker locations.

Finally, it’s worth nothing that, in the specific case of the Beosound Theatre, by setting the Speaker Distances and Speaker Levels for the Left and Right Front-firing outputs for your listening position, then you have automatically calibrated the virtual outputs. This is because the Speaker Distances and Speaker Levels are compensations for the ACTUAL outputs of the system, which are the ones producing the signal that simulate the virtual loudspeakers. This is the reason why the four virtual loudspeakers do not have individual Speaker Distances and Speaker Levels. If they did, they would have to be identical to the Left and Right Front-firing outputs’ values.

What is a “virtual” loudspeaker? Part 2

#91.2 in a series of articles about the technology behind Bang & Olufsen

In Part 1, I talked at how a binaural recording is made, and I also mentioned that the spatial effects may or may not work well for you for a number of different reasons.

Let’s go back to the free field with a single “perfect” microphone to measure what’s happening, but this time, we’ll send sound out of two identical “perfect” loudspeakers. The distances from the loudspeakers to the microphone are identical. The only difference in this hypothetical world is that the two loudspeakers are in different positions (measuring as a rotational angle) as shown in Figure 1.

Figure 1: Two identical, “perfect” loudspeakers in a free field with a single “perfect” microphone.

In this example, because everything is perfect, and the space is a free field, then output of the microphone will be the sum of the outputs of the two loudspeakers. (In the same way that if your dog and your cat are both asking for dinner simultaneously, you’ll hear dog+cat and have to decide which is more annoying and therefore gets fed first…)

Figure 2: The output from the microphone is the sum of the outputs from the two loudspeakers. At any moment in time, the value of the top plot + the value of the middle plot = the value of the bottom plot.

IF the system is perfect as I described above, then we can play some tricks that could be useful. For example, since the output of the microphone is the sum of the outputs of the two loudspeakers, what happens if the output of one loudspeaker is identical to the other loudspeaker, but reversed in polarity?

Figure 3: If the output of Loudspeaker 1 is exactly the same as the output of Loudspeaker 2 except for polarity, then the sum (the output of the microphone) is always 0.

In this example, we’re manipulating the signals so that, when they add together, you nothing at the output. This is because, at any moment in time, the value of Loudspeaker 2’s output is the value of Loudspeaker 1’s output * -1. So, in other words, we’re just subtracting the signal from itself at the microphone and we get something called “perfect cancellation” because the two signals cancel each other at all times.

Of course, if anything changes, then this perfect cancellation won’t work. For example, if one of the loudspeakers moves a little farther away than the other, then the system is broken, as shown below.

Figure 4: A small shift in time in the output of Loudspeaker 2 cases the cancellation to stop working so well.

Again, everything that I’ve said above only works when everything is perfect, and the loudspeakers and the microphone are in a free field; so there are no reflections coming in and ruining everything.

We can now combine these two concepts:

  1. using binaural signals to simulate a sound source in a location (although this would normally be done using playback over earphones to keep it simple) and
  2. using signals from loudspeakers to cancel each other at some location in space as a

to create a system for making virtual loudspeakers.

Let’s suspend our adherence to reality and continue with this hypothetical world where everything works as we want… We’ll replace the microphone with a person and consider what happens. To start, let’s just think about the output of the left loudspeaker.

Figure 5: The output of the left loudspeaker reaches both ears with different time/frequency characteristics caused by the HRTF associated with that sound source location.

If we plot the impulse responses at the two ears (the “click” sound from the loudspeaker after it’s been modified by the HRTFs for that loudspeaker location), they’ll look like this:

Figure 6: The impulse responses of the HRTFs for a sound source at 30º left of centre.

What if were were able to send a signal out of the right loudspeaker so that it cancels the signal from the left loudspeaker at the location of the right eardrum?

Figure 7: What if we could cancel the signal from the left loudspeaker at the right ear using the right loudspeaker?

Unfortunately, this is not quite as easy as it sounds, since the HRTF of the right loudspeaker at the right ear is also in the picture, so we have to be a bit clever about this.

So, in order for this to work we:

  • Send a signal out of the left loudspeaker.
    We know that this will get to the right eardrum after it’s been messed up by the HRTF. This is what we want to cancel…
  • …so we take that same signal, and
    • filter it with the inverse of the HRTF of the right loudspeaker
      (to undo the effects of the HRTF of the right loudspeaker’s signal at the right ear)
    • filter that with the HRTF of the left loudspeaker at the right ear
      (to match the filtering that’s done by your head and pinna)
    • multiply by -1
      (so that it will cancel when everything comes together at your right eardrum)
    • and send it out the right loudspeaker.

Hypothetically, that signal (from the right loudspeaker) will reach your right eardrum at the same time as the unprocessed signal from the left loudspeaker and the two will cancel each other, just like the simple example shown in Figure 3. This effect is called crosstalk cancellation, because we use the signal from one loudspeaker to cancel the sound from the other loudspeaker that crosses to the wrong side of your head.

This then means that we have started to build a system where the output of the left loudspeaker is heard ONLY in your left ear. Of course, it’s not perfect because that cancellation signal that I sent out of the right loudspeaker gets to the left ear a little later, so we have to cancel the cancellation signal using the left loudspeaker, and back and forth forever.

If, at the same time, we’re doing the same thing for the other channel, then we’ve built a system where you have the left loudspeaker’s signal in the left ear and the right loudspeaker’s signal in the right ear; just like a pair of headphones!

However, if you get any of these elements wrong, the system will start to under-perform. For example, if the HRTFs that I use to predict your HRTFs are incorrect, then it won’t work as well. Or, if things aren’t time-aligned correctly (because you moved) then the cancellation won’t work.

on to Part 3

What is a “virtual” loudspeaker? Part 1

#91.1 in a series of articles about the technology behind Bang & Olufsen

Without connecting external loudspeakers, Bang & Olufsen’s Beosound Theatre has a total of 11 independent outputs, each of which can be assigned any Speaker Role (or input channel). Four of these are called “virtual” loudspeakers – but what does this mean? There’s a brief explanation of this concept in the Technical Sound Guide for the Theatre (you’ll find the link at the bottom of this page), which I’ve duplicated in a previous posting. However, let’s dig into this concept a little more deeply.

To begin, let’s put a “perfect” loudspeaker in a free field. This means that it’s in a space that has no surfaces to reflect the sound – so it’s an acoustic field where the sound wave is free to travel outwards forever without hitting anything (or at least appear as this is the case). We’ll also put a “perfect” microphone in the same space.

Figure 1: A loudspeaker and a microphone (the circle) in a free field: an infinite space completely free of reflective surfaces.

We then send an impulse; a very short, very loud “click” to the loudspeaker. (Actually a perfect impulse is infinitely short and infinitely loud, but this is not only inadvisable but impossible, and probably illegal.)

Figure 2: The “click” signal that’s sent to the input of the loudspeaker.

That sound radiates outwards through the free field and reaches the microphone which converts the acoustic signal back to an electrical one so we can look at it.

Figure 3: The “click” signal that is received at the microphone’s location and sent out as an electrical signal.

There are three things to notice when you compare Figure 3 to Figure 2:

  • The signal’s level is lower. This is because the microphone is some distance from the loudspeaker.
  • The signal is later. This is because the microphone is some distance from the loudspeaker and sound waves travel pretty slowly.
  • The general shape of the signals are identical. This is because I said that the loudspeaker and the microphone were both “perfect” and we’re in a space that is completely free of reflections.

What happens if we take away the microphone and put you in the same place instead?

Figure 4: The microphone has been replaced by something more familiar.

If we now send the same click to the loudspeaker and look at the “outputs” of your two eardrums (the signals that are sent to your brain), these will look something like this:

Figure 5: The outputs of your two eardrums with the same “click” signal from the loudspeaker.

These two signals are obviously very different from the one that the microphone “hears” which should not be a surprise: ears aren’t microphones. However, there are some specific things of which we should take note:

  • The output of the left eardrum is lower than that of the right eardrum. This is largely because of an effect called “head shadowing” which is exactly what it sounds like. The sound is quieter in your left ear because your head is in the way.
  • The signal at the right eardrum is earlier than at the left eardrum. This is because the left eardrum is not only farther away, but the sound has to go around your head to get there.
  • The signal at the right eardrum is earlier than the output of the microphone output (in Figure 3) because it’s closer to the loudspeaker. (I put the microphone at the location of the centre of the simulated head.) Similarly the left ear output is later because it’s farther away.
  • The signal at the right eardrum is full of spikes. This is mostly caused by reflections off the pinna (the flappy thing on the side of your head that you call your “ear”) that arrive at slightly different times, and all add together to make a mess.
  • The signal at the left eardrum is “smoother”. This is because the head itself acts as a filter reducing the levels of the high frequency content, which tends to make things less “spiky”.
  • Both signals last longer in time. This is the effect of the ear canal (the “hole” in the side of your head that you should NOT stick a pencil in) resonating like a little organ pipe.

The difference between the signals in Figures 2 and 4 is a measurement of the effect that your head (including your shoulders, ears/pinnae) has on the transfer of the sound from the loudspeaker to your eardrums. Consequently, we geeks call it a “head-related transfer function” or HRTF. I’ve plotted this HRTF as a measurement of an impulse in time – but I could have converted it to a frequency response instead (which would include the changes in magnitude and phase for different frequencies).

Here’s the cool thing: If I put a pair of headphones on you and played those two signals in Figure 5 to your two ears, you might be able to convince yourself that you hear the click coming from the same place as where that loudspeaker is located.

Although this sounds magical, don’t get too excited right away. Unfortunately, as with most things in life, reality tends to get in the way for a number of reasons:

  • Your head and ears aren’t the same shape as anyone else’s. Your brain has lived with your head and your ears for a long time, and it’s learned to correlate your HRTFs with the locations of sound sources. If I suddenly feed you a signal that uses my HRTFs, then this trick may or may not work, depending on how similar we are. This is just like borrowing someone else’s glasses. If you have roughly the same prescription, then you can see. However, if the prescriptions are very different, you’ll get a headache very quickly.
  • In reality, you’re always moving. So, even if the sound source is not moving, the specific details of the HRTFs are always changing (because the relative positions and angles to your ears are changing) but my system doesn’t know about this – so I’m simulating a system where the loudspeaker moves around you as you rotate your head. Since this never happens in real life, it tends to break the simulation.
  • The stuff I showed above doesn’t include reflections, which is how you determine distance to sources. If I wanted to include reflections, each reflection would have to have its own HRTF processing, depending on its angle relative to your head.

However, hypothetically, this can work, and lots of people have tried. The easiest way to do this is to not bother measuring anything. You just take a “dummy head” -a thing that is the same size as an average human head (maybe with an average torso) and average pinnae* – but with microphones where the eardrums are – and you plunk it down in a seat in a concert hall and record the outputs of the two “ears”. You then listen to this over earphones (we don’t use headphones because we want to remove your pinnae from the equation) and you get a “you are there” experience (assuming that the dummy head’s dimensions and shape are about the same as yours). This is what’s known as a binaural recording because it’s a recording that’s done with two ears (instead of two or more “simple” microphones).

If you want to experience this for yourself, plug a pair of headphones into your computer and do a search for the “Virtual Barber Shop” video. However, if you find that it doesn’t work for you, don’t be upset. It just means that you’re different: just like everyone else.* Typically, recordings like this have a strange effect of things sounding very close in the front, and farther away as sources go to the sides. (Personally, I typically don’t hear anything in the front. All of the sources sound like they’re sitting on the back of my neck and shoulders. This might be because I have a fat head (yes, yes… I know…) and small pinnae (yes, yes…. I know…) – or it might indicate some inherent paranoia of which I am not conscious.)

* Of course, depressingly typically, it goes without saying that the sizes and shapes of commercially-available dummy heads are based on averages of measurements of men only. Neither women nor children are interested in binaural recordings or have any relevance to such things, apparently…

on to Part 2

“High-Res” Audio: Part 11: How high can you go?

Part 1
Part 2
Part 3
Part 4
Part 5
Part 6
Part 7
Part 8a
Part 8b
Part 9
Part 10

If you you get an audiometry test done, you’ll be shown into a small room, about the size of a public bathroom stall. Someone will put a pair of headphones on you, and pass you a small handle with a button. Your instructions are to press the button if you hear a tone. Then the audiometrist will leave the room, closing the door, and you’ll suddenly realise that if there’s any noise in this room, it’s because you’re making it.

Then you hear a beep in your left ear. You press the button. You hear a quieter beep. Press. Quieter beep. Press…. …. …. Beep, press… …. …. …. Beep, press…. New frequency beep, loud again. Press… and so on.

What’s happening here is that you’re presented with a sine tone at some frequency, probably loud enough for you to hear. You press. The tone gets quieter, and you press again. Eventually, the tone is so quiet that you cannot hear it (this is normal) so you don’t press. So, the tone gets louder, and you press. Then it gets quieter again, until you can’t hear it again.

By crossing over that threshold of “can hear” and “can’t hear” a couple of times, the audiometrist finds out whether or not you got lucky… If you bottom out at the same level a couple of times in a row, then that’s your threshold of hearing at that frequency in that ear.

The frequency changes (usually by 1 octave, but sometimes less), and the whole process is repeated.

If you get a full test done, then this is probably done at 9 frequencies (250, 500, 1k, 1.5k, 2k, 3k, 4k, 6k, and 8kHz) in both ears individually – 18 tests in all.

You’ll then be given a sheet of paper, or at least shown a plot of your hearing threshold. Typically, if you have “normal” hearing (whatever that means) your thresholds will all be sitting on a horizontal line marked 0 dB. If you’re “better than normal” then you get a negative score, if you’re “worse than normal” you get a positive score.

What does this mean?

Let’s start over.

If a lot of people do this test, and we only test at 1 kHz, we’ll find out that, after the results are averaged, the group can hear the 1 kHz sine tone when the change in air pressure at the ear entrance is 20 µPa. We’re not going to talk about what this means other than to say that “sound is a change in air pressure over time, and that pressure is measured in pascals, abbreviated Pa”. Needless to say, 20 µPa is pretty quiet, since it’s the quietest sound a group of people can hear at 1 kHz when you take their average.

If you did that test at a much lower frequency, you would find out that people aren’t as good at hearing quiet sounds. In other words, at 100 Hz, the sine tone has to be louder than 20 µPa for people to hear it.

The same is true if you repeated the test at a much higher frequency – say, 10,000 Hz.

If you did this test at a lot of frequencies, then you’d find out that, on average, the threshold of hearing for a human follows the bottom red line of the plot in Figure 1, borrowed from Wikipedia.

Figure 1: The bottom red curve is the average threshold of hearing for a human being.

That bottom plot shows the threshold of hearing for different frequencies, plotted in dB SPL. Notice that, at 1 kHz, the line is at 0 dB SPL. This is because 0 dB SPL is defined to be the average threshold of hearing of a human at 1 kHz, which is 20 µPa. So, it’s not an accident…

Looking at that plot, you can see that, in order to hear a sine tone at 20 Hz, the tone has got to be more than 70 dB louder (that’s a LOT louder). So, a microphone “sees” a 73 dB SPL, 20 Hz sine tone as being louder than a 0 dB SPL, 1 kHz sine tone – but as far as you’re concerned, they’re both “the quietest sound you can hear” – therefore, they’re the same level.

If we take that threshold of hearing curve, and we play tones at those levels for those frequencies, then you should “just be able to” hear them. So, we’ll call those levels “0 dB” – since it’s the same as what is expected of you.

In other words, the piece of paper you got from the audiometrist tells you how much above or below that red threshold of hearing YOU sit.

Now, let’s back up a bit.

  1. I said that, in your test, you only went up to 8 kHz. This is because, above that (and possibly even before that) the headphones might not be trust-worthy, and even a tiny movement (say a couple of millimetres) in the position of the headphones will have a (relatively) big effect on the level at your eardrum. So, rather than get people worried about losing their hearing at 20,000 Hz (when, in fact, they were actually just wearing the headphones 1 mm too far forward), you won’t get tested.
  2. Notice how variable that threshold of hearing line is. There are big changes in level over the “audible” frequency range.
  3. Remember that the threshold of hearing curve is an AVERAGE of a lot of people. Just like no one has 2.6 children, no one has this exact response. And, if you are some freak of nature and you DO have exactly that response, you don’t for long… we all get old…
  4. Notice how that threshold of hearing curve only goes up to about 16 kHz, and above that it says “estimated”. See point #1.

Now, you should know that your ability to hear a sine tone at some frequency is defined as how your ability compares to an expectation based on an average, within a relatively small frequency band: 250 to 8 kHz.

Then you look at a textbook or you read a website that says “humans can hear from 20 Hz to 20 kHz”, which is not enough information to be either true or false… It’s like saying “humans are usually between 0 and 10 m tall” which is also sort of true, but also adequately vague to be potentially worse-than-useless information.

The truth is, unfortunately, much more complicated… However, it’s fair to say that, in order for you to just hear a sine tone at 20 kHz, it would have to be much, much louder than one at 1 kHz. In fact, if I played a 20 kHz sine tone loud enough for you to hear, measured that level, and then played a 1 kHz sine tone for you at the same level, you’d probably punch me – after you had passed out due to the pain, woken up, hunted me down, and found me… (I’d already have run away by then….)

So what?

We humans like nice, tidy, answers. “It will rain tomorrow” is preferable to “there is a 70 – 80% chance of scattered showers in the afternoon tomorrow”. We even get mad when the information is correct, but we interpret it tidily… For example, we’ll complain about getting rained on in the middle of our hike, when there was only a 10% chance of rain. On the other hand, if there was a 10% chance of winning 1 Million dollars in the lottery, we’d all buy a ticket.

Anyways, once-upon-a-time, when the committee for inventing the compact disc was holding meetings, they said “what should the sampling rate be?” and someone said “at least 40 kHz, because we can hear up to 20 kHz”. (The reason it’s 44100 is related to the fact that the bits were stored as black and white stripes on video tape, and NTSC and PAL come close to meeting each other close to that number, when you look at the numbers of lines per field and frames per second.)

Of course, like any first-generation thing, digital recording equipment wasn’t very good at the start (back around 1980 or so) – so the first DDD recordings that were released on CD sounded… well…. weird. There was quantisation distortion because they hadn’t figured out dither yet, only 12 or 13 of the bit values were working properly on the ADC’s, the anti-aliasing filters were implemented as analogue circuits, so they let some stuff through that aliased, and they rang (“sang along”) with the signal at a high frequency… All of that added up to “weird” – possibly even “bad”. Then, people who had good equipment (high-end turntables or, even better, 1/4″ tape running at 30 ips) listened to this new format, decided it was bad, and that was that.

Some of them asked “why is is bad?” and one answer they came up with was the band limiting… If the system can’t capture or store or play materials above 20 kHz, then it’s useless… Right? Maybe…

Then, instruments were put in front of measurement microphones and spectra were measured – and the proof was in. Trumpets with harmon (wah-wah) mutes, when pointing directly at the microphone, contain harmonics as high as 50 kHz! This must explain why CDs sound bad! Right? Maybe…

Then Rupert Neve did a demo at an AES (Audio Engineering Society) convention where he played people two tones. Both were at 7 kHz, but one was a sine wave and the other was a square wave (at some level). The question was: have a listen and tell me which is which. The results were the same as if everyone was just guessing. (Remember that, in order to make a square wave, you need to add odd harmonics – so the lowest-frequency content difference between a 7 kHz sine wave and a 7 kHz square wave is at 21 kHz.) Proof that we don’t need to go above 20 kHz, right? Maybe…

Some years ago, I took some “high resolution” audio files and measured their spectral content. One particularly interesting result is shown in Figures 2, below.

Figure 2: The spectral content of a 96/24 “high resolution” audio file I bought.

Look at that spike in the top end – around 20 kHz. What musical instrument makes that sound? The answer is “no musical instrument makes that sound – at least none of the baroque instruments in that recording make that sound. As I wrote back in 2014:

 If you’re wondering what it might be, I asked a bunch of smart friends, and the best explanation we can come up with is that it’s noise from a switched-mode power supply that is somehow bleeding into the recording. HOW it’s bleeding into the recording is a potentially interesting question for recording engineers. One possibility is that one of the musicians was charging up a phone in the room where the microphones were – and the mic’s just picked up the noise. Another possibility is that the power supply noise is bleeding electrically into the recording chain – maybe it’s a computer power supply or the sound card and the manufacturer hasn’t thought about isolating this high frequency noise from the audio path. Or, maybe it’s something else.

Interestingly, this is a conflict of two engineers. The designer of the power supply (assuming that’s what it is…) said “I’ll put the switching frequency above 20 kHz so that no one will hear it” and the recording engineer said “I’ll record this at 96 kHz so that people can get the content they’re missing…” The problem is that the content you’re missing is something you don’t want…

Similarly, if you listen to Eric Clapton’s “Unplugged” album with headphones or loudspeakers that have a low-enough low-frequency range, you’ll hear a loud thump, thump, thump going along with the music. This is the sound of someone tapping their foot on a temporary stage floor, shaking a vocal microphone. In my not-very-humble opinion, that should never have made it out to the public release. However, my guess is that the speakers it was mastered on didn’t go low enough… (OR, it was an artistic decision, and I would have done it differently.) Assuming that I’m right, then this is a second example where a “better” system sounds “worse”.

Of course, through all of this, I have assumed that your loudspeakers or headphones can produce the signals that we’re talking about in the direction that you’re sitting in, and that those signals are not being masked by other sounds in the room (like phone chargers singing…) However, to complicate things with reality would just be too far to go today…

Conclusions?

I don’t have any, but I have some questions and (as usual) some opinions…

  • Does a harmon mute on a trumpet produce energy at 50 kHz, if you’re sitting right in front of it?
    Yes.
  • Do you want to sit right in front of a trumpet with a harmon mute?
    Debatable.
  • Can a high-res audio recording include the sound of a phone charger?
    Yes.
  • Do you want to have an expensive recording of a baroque ensemble with obligato phone charger?
    Probably not – the charger is not in Buxtehude’s original score as far as I can see.
  • Can you hear the difference between a 7 kHz sine and a 7 kHz square wave?
    Depends on the speaker / headphone, the listening position, the background noise level, and whether or not you were out clubbing last night. Heads or tails?
  • Will you feel better by knowing that your file contains “audio” content above 20 kHz? Probably.
    Placebos have been known to work bigger miracles than this. (But don’t forget the stuff I said about sampling rate converters earlier…)