#94 in a series of articles about the technology behind Bang & Olufsen
This was an online lecture that I did for the UK section of the Audio Engineering Society.
#94 in a series of articles about the technology behind Bang & Olufsen
This was an online lecture that I did for the UK section of the Audio Engineering Society.
As I showed in Part 5, the phase response of a loudspeaker driver in a closed cabinet is different from one in a ported cabinet in the low frequency region because, the low frequency output of the ported system is actually coming from the port, not the driver.
If we take the phase response plots from the two systems shown in Part 5 and put them on the same graph, the result is Figure 1.
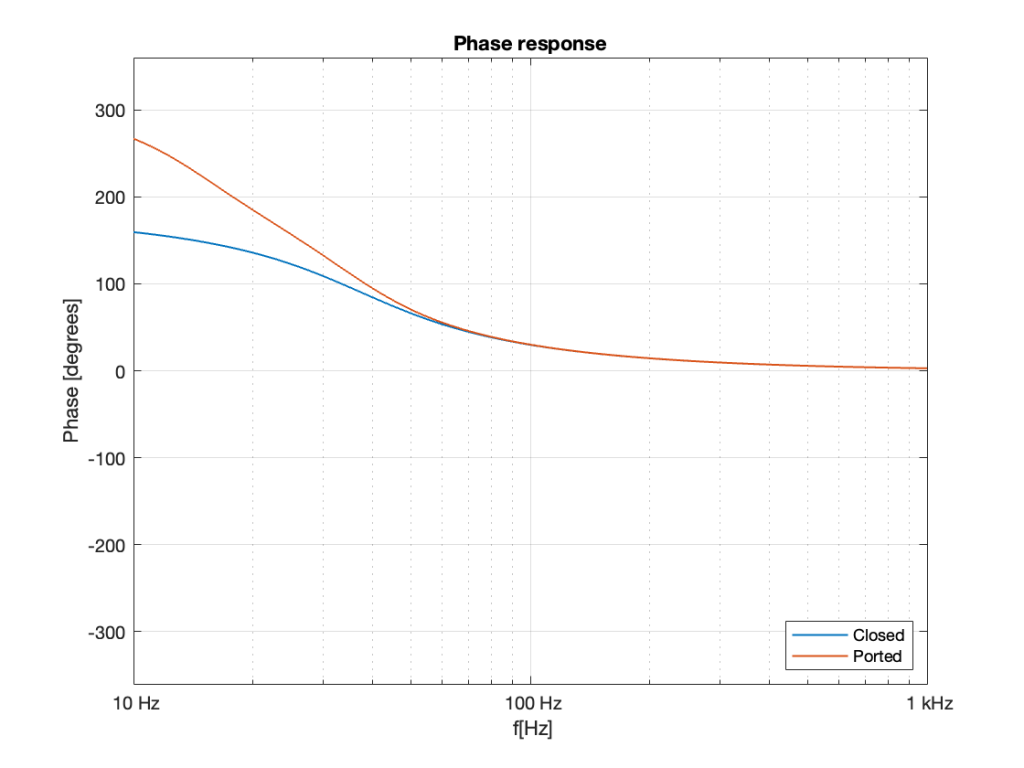
If we calculate the difference in these two plots by subtracting the blue curve from the red curve at each frequency then we can see that a ported cabinet is increasingly out of phase relative to a sealed cabinet as you go lower and lower in frequency. This difference is shown in Figure 2.
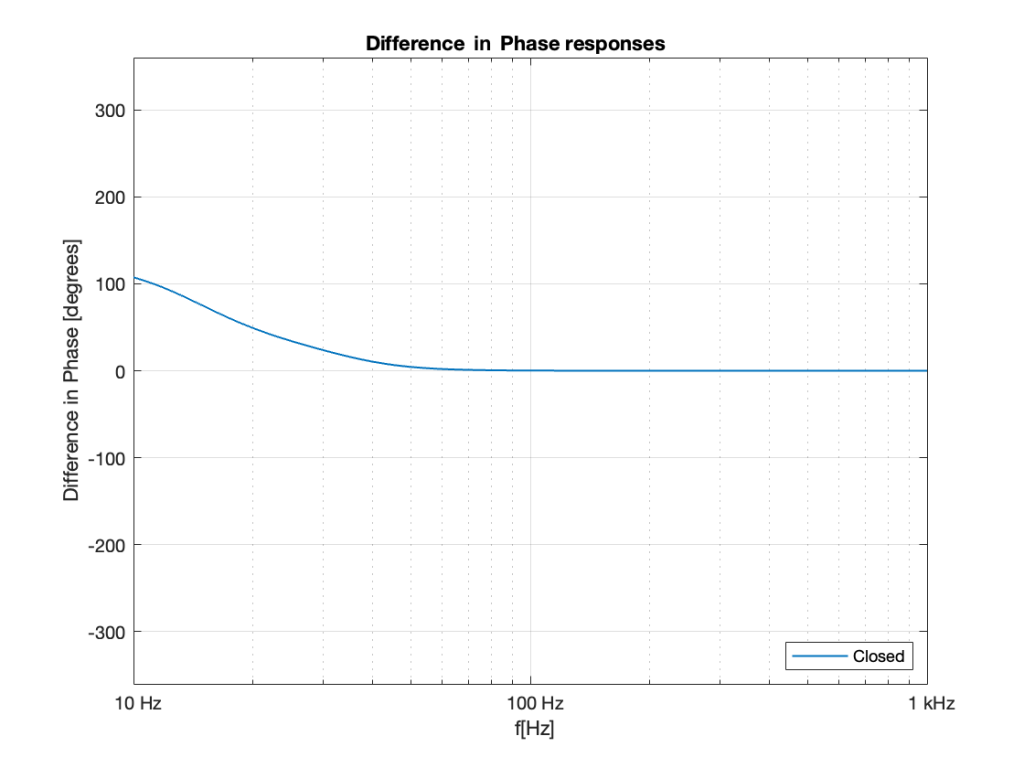
Now, don’t look at that graph and say “but you never get to 180º so what’s the problem?” All of the plots I’ve shown in this series are for one specific driver in one specific enclosure, with and without a port of one specific diameter and length. I could have been more careful and designed two different enclosures (with and without a port) that does get to 180º (or something else up to 180º).
In other words: “results may vary”. Every loudspeaker in every cabinet has some magnitude response and some phase response (these are directly related to each other), and they’ll all be different by different amounts. (This is also the reason why I’m neglecting to talk about the fact that, as you go lower in frequency, the ported loudspeaker also drops faster in output level, so even if it were a full 180º out of phase, it would cancel less and less when combined with the sealed cabinet loudspeaker.)
The point of all of this was to show that, if you take two different loudspeakers with two different enclosure types, you get two different phase responses, particularly in the low frequency region.
This means that if you take those two loudspeaker types (the original question that inspired this series was specifically about mixing Beolab 9, Beolab 20, and Beolab 2 in a system where all of those loudspeakers are “helping” to produce the bass) and play identical signals from them in the same room, it’s not only possible, but highly likely that they will wind up cancelling each other. This results in LESS bass instead of MORE, ignoring all other effects like loudspeaker placement, room modes, and so on.
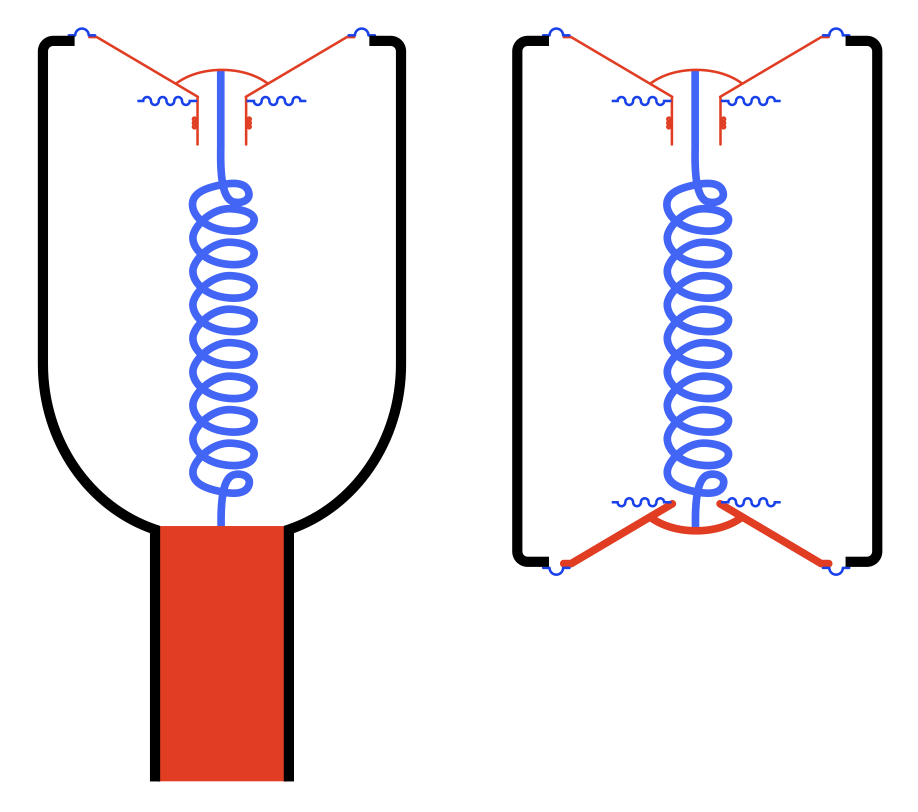
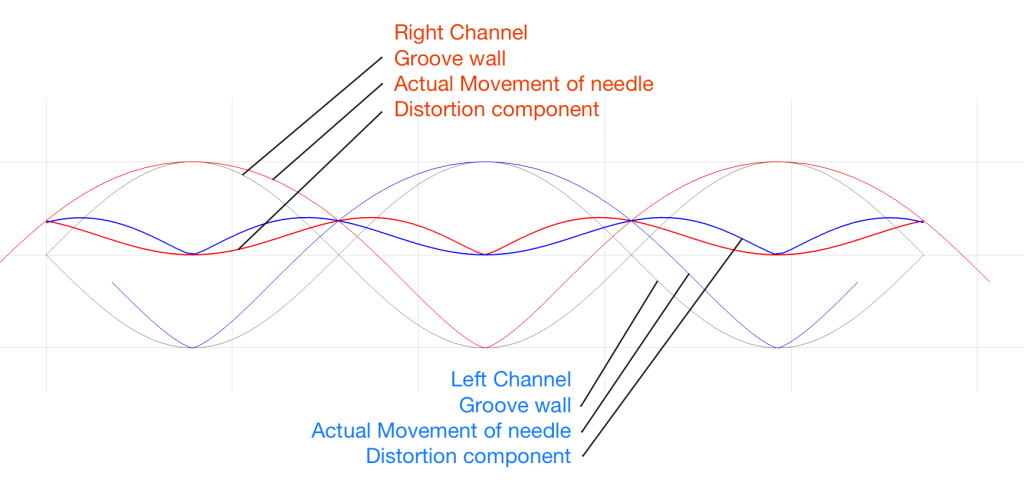
Take a look at Figure 3. I’ve shown a conceptual drawing of a ported loudspeaker (showing the mass of the air in the port as a red rectangle) on the left and a loudspeaker with a slave driver (on the bottom – notice it’s missing a former and voice coil, and the diaphragm is thicker to make it heavy) on the right.
This should make it intuitively obvious that a ported loudspeaker and an enclosure with a slave driver are effectively identical. This raises the question of why you would do one rather than the other.
The advantages of using a port instead of a slave driver is that a port will be more “stable” on a production line (since all of the ports on all the loudspeakers you make will be identical in size) and they’ve very cheap to make. The disadvantage of a port is that if the velocity of the air moving in and out of it is too high, then you hear it “chuffing”, which is a noise caused by turbulence around the edges of the port. (If you blow across the top of a wine bottle, you don’t hear a perfect sine wave, you hear a very noisy “breathy” one. The noise is the chuffing.)
The advantage of a slave driver is that you don’t get any turbulence, and therefore no chuffing. A slave driver can also be heavier than the air in a port in a smaller space, so you can get the response of a large port in a smaller loudspeaker. There is a small disadvantage in the fact that there will be production line tolerance variations (but this is not really a big worry), and then there’s the price, which is much higher than a hole in a box.
This means that if you take anything I’ve said above about ported loudspeakers, and replace the word “port” with “slave driver” then it’s still true.
If you do have a surround system that not only has a bass management system, but is also capable of re-directing the bass to more loudspeakers than just your subwoofer (as is the case with all current Bang & Olfusen surround processors in the televisions), then all of this is important to remember. You can’t just send the bass to more loudspeakers and expect to get more output. You might get less.
This is true unless you have a Beosound Theatre. This is because the Theatre has an extra bit of processing in the signal path called “Phase Compensation” which applies an allpass filter to the outputs, compensating for the phase differences between loudspeakers in the low frequency region. So, in this one particular case, you should expect to get more output from more loudspeakers.
Let’s build a ported box and put a woofer in it. If we measure the magnitude responses of the individual outputs of the driver and the port as well as the total output of the entire loudspeaker, they might look like the three curves shown in Figure 1.

If you take a look at the curves at 1 kHz, you can see that the total output (the blue curve) is the same as the woofer’s output (the red curve) because the port’s output (the yellow curve) is so low that it’s not contributing anything.
As we come down in frequency, we see the output of the port coming up and the output of the driver coming down. At around 20 Hz, the port reaches its maximum output and the woofer reaches its minimum as a result. In fact that woofer’s output is about 15 dB lower than the port’s at that frequency.
As we go farther down in frequency, we can see that the woofer comes up and then starts to drop again, but the port just drops in level the lower we go.
Now look at the total output (the blue curve) from 20 Hz and down. Notice that the total output of the system from 20 Hz down to about 15 Hz is LOWER than the output of the port alone. As you go below about 15 Hz, you can see that the total output is lower than either the woofer or the port.
This means that the port and the woofer are cancelling each other, just like I described in the previous part in this series. This can be seen when we look at their respective phase responses, shown in the middle plot in Figure 2. I’ve also plotted the difference in the woofer and the port phase responses in the bottom plot.
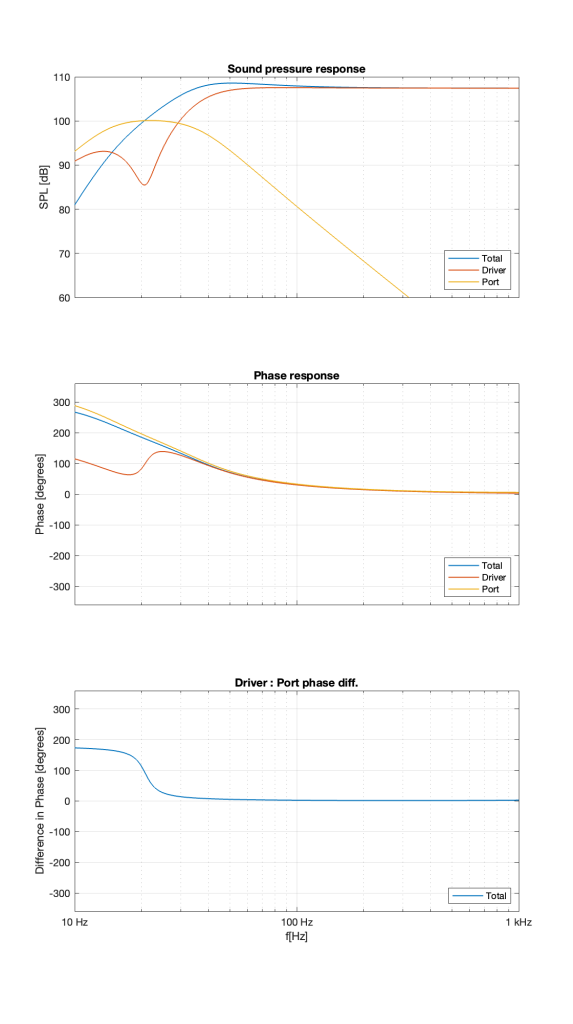
Notice that, below 20 Hz, the woofer and the port are about 180º apart. So, as the woofer moves out of the enclosure, the air in the port moves inwards, and the total sum is less than either of the two individual outputs.
What happens when you put a woofer in a sealed enclosure instead of one with a port? The responses from this kind of system are shown below in Figure 3.

The first thing that you’ll notice in the plots in Figure 3 is that there is only one curve in each graph. This is because the total output is the driver output.
You’ll also notice in the top plot that a woofer in a cabinet acts as a second-order high-pass filter because the cabinet is not too small for the driver. If the cabinet were smaller, then you’d see a peak in the response, but let’s say that I’m not that dumb…
Because it’s a second-order high-pass filter, it has a phase response that approaches 180º as you go down in frequency.
Now, compare that phase response in the low end of Figure 3 to the phase response of the low end in Figure 2. This is where we’re headed, since the purpose of all of this discussion is to talk about what happens when you have a system that combines sealed enclosures with ported ones. That brings us to Part 6.
In Part 1, I showed how a wine bottle behaves exactly like a mass on a spring where the mass is the cylinder of air in the bottle’s neck and the spring is the air inside the bottle itself.
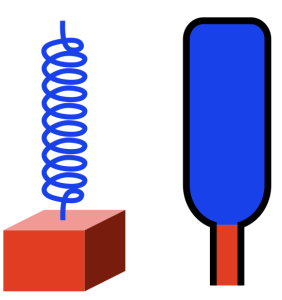
I also showed how a loudspeaker driver (like a woofer) in a closed box is the same thing, where the spring is the combination of the surround, the spider and the air in the box.
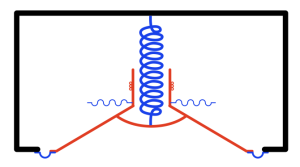
But what happens if the speaker enclosure is not sealed, but instead is open to the outside world through a “port” which is another way of saying “a tube”. Then, conceptually, you are combining the loudspeaker driver with the wine bottle like I’ve shown in Figure 3.
If I were to show this with all the masses in red and all the springs in blue, it would look like Figure 4.
Now things are getting a little complicated, so let’s take things slowly… literally.
If the loudspeaker driver in Figure 4 moves into the cabinet very slowly (say, you push it with your fingers or you play a very low frequency with an electrical signal), then the air that it displaces in of the bottle (the enclosure) will just push the plug of air out the bottle’s neck (the port). The opposite will happen if you pull the driver out of the enclosure: you’ll suck air into the port.
If, instead you move the driver back and forth very quickly (by playing a very high frequency) then the inertia of the air inside the cabinet (shown as the big blue spring in the middle) prevents it from moving down near the port. In fact, if the frequency is high enough, then the air at the entrance of the port doesn’t move at all. This means that, for very high frequencies, the system will behave exactly the same as if the enclosure were sealed.
But somewhere between the very low frequencies and the very high frequencies, there is a “magic” frequency where the air in the port resonates, and there, things don’t behave intuitively. At that frequency, whenever the driver is trying to move into the enclosure, the air in the port is also moving into the enclosure. And, although the air has less mass than the driver, it’s free to move more. The end result is that, at the port’s resonant frequency, the driver (in theory) doesn’t move at all*, and the air in the port is moving a lot.**
In other words, you can think of a single driver in a ported cabinet as being basically the same as a two-way loudspeaker, where the woofer (for example) is one driver and the port is the other “driver”.
If you look at this as a magnitude response (the correct term for “frequency response” for this discussion), you can think of the woofer having one response, the port having a different response, and the two adding together somehow to produce a total response for the entire loudspeaker.
However, as you can see from the short 4-point list above, something happens with the phase of the signal at different frequencies. This is most obvious in the “very low frequency” part, where the woofer’s and the port’s outputs are 180º out of phase with each other.
In Part 5 we’ll look at these different components of the total output separately, both in terms of magnitude and phase responses (which, combined are the frequency response).
* Okay okay…. I say “the driver (in theory) doesn’t move at all” and “all of the sound is coming from the movement of the air in and out of the port” which is a bit of an exaggeration. But it’s not MUCH of an exaggeration…
** This is an oversimplified explanation. The slightly less simplified version is that the air inside the cabinet is acting like a spring that’s getting squeezed from two sides: the driver and the air in the port. The driver “sees” the “spring” (the air in the box) as pushing and pulling on it just as much as its pulling and pushing, so it can’t move (very much…).
Before starting on this portion of the series, I’ll ask you to think about how little energy (or movement) it takes to get a resonant system oscillating. For example, if you have a child on a swing, a series of very gentle pushes at the right times can result in them swinging very high. Also, once the child is swinging back and forth, it takes a lot of effort to stop them quickly.
So far, we’ve seen that a loudspeaker driver in a closed cabinet can be thought of as just a mass on a spring, and, as a result, it has some natural resonance where it will oscillate at some frequency.
The driver is normally moved by sending an electrical signal into its voice coil. This causes the coil to produce a magnetic field and, since it’s already sitting in the magnetic field of a permanent magnet, it moves. The surround and spider prevent it from moving sideways, so it can only move outwards (if we send electrical current in one direction) or inwards (if we send current in the other direction).
When you try to move the driver, you’re working against a number of things:
These three things can be considered separately from each other as a static effect. In other words:
But, if you’re pushing AND pulling the loudspeaker driver there is another effect that’s dynamic.
When you’re moving the driver at a VERY low frequency, you’re mostly working against the “spring” which is probably quite easy to do. So, at a low frequency, the driver is pretty easy to move, and it’s moving so slowly that it doesn’t push back electrically. So, it does not impede the flow of current through the voice coil.
When you’re moving the driver at a VERY high frequency, you’re mostly working against the inertia of the moving parts and the adjacent air molecules. The higher the frequency, the harder it is to move the driver.
However, when you’re trying to moving the driver at exactly the resonant frequency of the driver, you don’t need much energy at all because it “wants” to move at that same rate. However, at that frequency, the voice coil is moving in the magnetic field of the permanent magnet, and it generates electricity that is trying to move current in the opposite direction of what your amp is going. In other words, at the driver’s resonant frequency, when you’re trying to push current into the voice coil, it generates a current that pushes back. When you try to pull current out of the voice coil, it generates a current that pulls back.
In other words, at the driver’s resonant frequency, your amplifier “sees” the driver as as a thing that is trying to impede the flow of electrical current. This means that you get a lot of movement with only a little electrical current; just like the child on the swing gets to go high with only a little effort – but only at one frequency.
This is a nice, simple case where you have a moving mass (the moving parts of the driver) and a spring (the surround, spider, and air in the sealed box). But what happens when the speaker has a port?
On to Part 4…
Let’s look at a typical moving coil loudspeaker driver like the woofer shown in Figure 1.

If I were to draw a cross-section of this and display it upside-down, it would look like Figure 2.
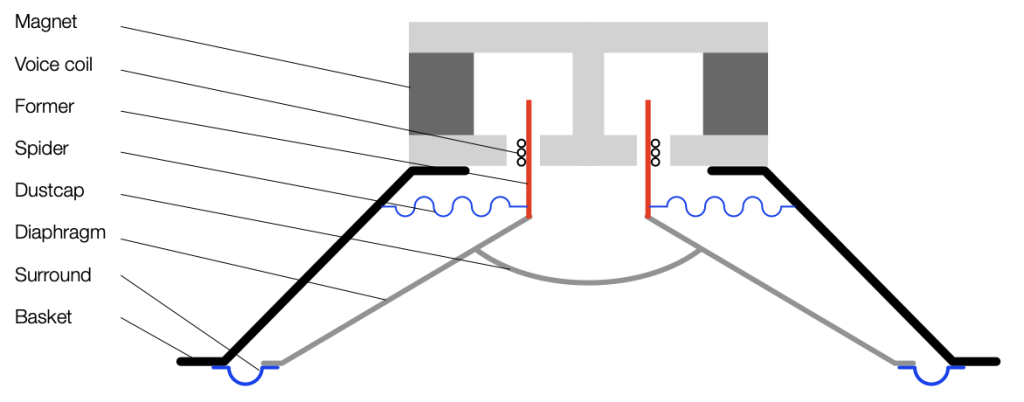
Typically, if we send a positive voltage/current signal to a driver (say, the attack of a kick drum to a woofer) then it moves “forwards” or “outwards” (from the cabinet, for example). It then returns to the rest position. If we send it a negative signal, then it moves “backwards” or “inwards”. This movement is shown in Figure 3.

Notice in Figure 3 that I left out all of the parts that don’t move: the basket, the magnet and the pole piece. That’s because those aren’t important for this discussion.
Also notice that I used only two colours: red for the moving parts that don’t move relative to each other (because they’re all glued together) and blue for the stretchy parts that act as a spring. These colours relate directly to the colours I used in Part 1, because they’re doing exactly the same thing. In other words, if you hold a woofer by the basket or magnet, and tap it, it will “bounce” up and down because it’s just a mass suspended by a spring. And, just like I talked about in Part 1, this means that it will oscillate at some frequency that’s determined by the relationship of the mass to the spring’s compliance (a fancy word for “springiness” or “stiffness” of a spring. The more compliant it is, the less stiff.) In other words, I’m trying to make it obvious that Figure 3, above is exactly the same as Figures 3 and 5 in Part 1.
However, it’s very rare to see a loudspeaker where the driver is suspended without an enclosure. Yes, there are some companies that do this, but that’s outside the limits of this discussion. So, what happens when we put a loudspeaker driver in a sealed cabinet? For the purposes of this discussion, all it means is that we add an extra spring attached to the moving parts.

I’ve shown the “spring” that the air provides as a blue coil attached to the back of the dust cap. Of course, this is not true; the air is pushing against all surfaces inside the loudspeaker. However, from the outside, if you were actually pushing on the front of the driver with your fingers, you would not be able to tell the difference.
This means that the spring that pushes or pulls the loudspeaker diaphragm back into position is some combination of the surround (typically made of rubber nowadays), the spider (which might be made of different things…) and the air in the sealed cabinet. Those three springs are in parallel, so if you make one REALLY stiff (or lower its compliance) then it becomes the important spring, and the other two make less of a difference.
So, if you make the cabinet too small, then you have less air inside it, and it becomes the predominant spring, making the surround and spider irrelevant. The bigger the cabinet, the more significant a role the surround and spider play in the oscillation of the system.
Sidebar: If you are planning on making a lot of loudspeakers on a production line, then you can use this to your advantage. Since there is some variation in the compliance of the surround and spider from driver-to-driver, then your loudspeakers will behave differently. However, if you make the cabinet small, then it becomes the most important spring in the system, and you get loudspeakers that are more like each other because their volumes are all the same.
Remember from part 1 that if you increase the stiffness of the spring, then the resonant frequency of the oscillation will increase. It will also ring for longer in time. In practical terms, if you put a woofer in a big sealed cabinet and tap it, it will sound like a short “thump”. But if the cabinet is too small, then it will sound like a higher-pitched and longer-ringing “bonnnnnnnggggg”.
So far, we’ve only been talking about physical things: masses and springs. In the next part, we’ll connect the loudspeaker driver to an amplifier and try to push and pull it with electrical signals.
I made a comment on a forum this week, commenting that, if you mix loudspeakers with closed cabinets with loudspeakers with ported cabinets (or slave drivers), the end result can be a reduction in total output: less sound from more loudspeakers. Of course, the question is “why?” and the short answer is “due to the phase mismatching of the loudspeakers”.
This is the long answer.
Before we begin, we have to get an intuitive understanding of what a ported loudspeaker is. (Note that I’ll keep saying “ported loudspeaker”, but the principle also applies to loudspeakers with slave drivers, as I’ll explain later.) Before we get to a ported loudspeaker, we need to talk about Helmholtz resonators.
Take a block that’s reasonably heavy and hang it using a spring so that it looks like this:
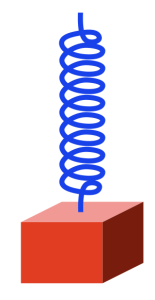
The spring is a little stretched because the weight of the block (which is the result of its mass and the Earth’s gravity) is pulling downwards. (We’ll ignore the fact that the spring is also holding up its own weight. Let’s keep this simple…) However, it doesn’t fall to the floor because the spring is pulling upwards.
Now pull downwards on the block, so it will look like the example on the right in the figure below.

The spring is stretched because we’re pulling down on the block. The spring is also pulling upwards more, since it’s pulling against the weight of the block PLUS the force that you’re adding in a downwards direction.
Now you let go of the block. What happens?
The spring is pulling “too hard” on the block, so the block starts rising back to where it started (we’ll call that the “resting position”). However, when it gets there, it has inertia (a body in motion tends to stay in motion… until it hits something big…) so it doesn’t stop. As a result, it moves upwards, higher than the resting position. This squeezes the spring until it gets to some point, at which time the block stops, and then starts going back downwards. When it returns to the resting position, it still has inertia, so it passes that point and goes too far down again. I’ve shown this as a series of positions from left to right in the figure below.
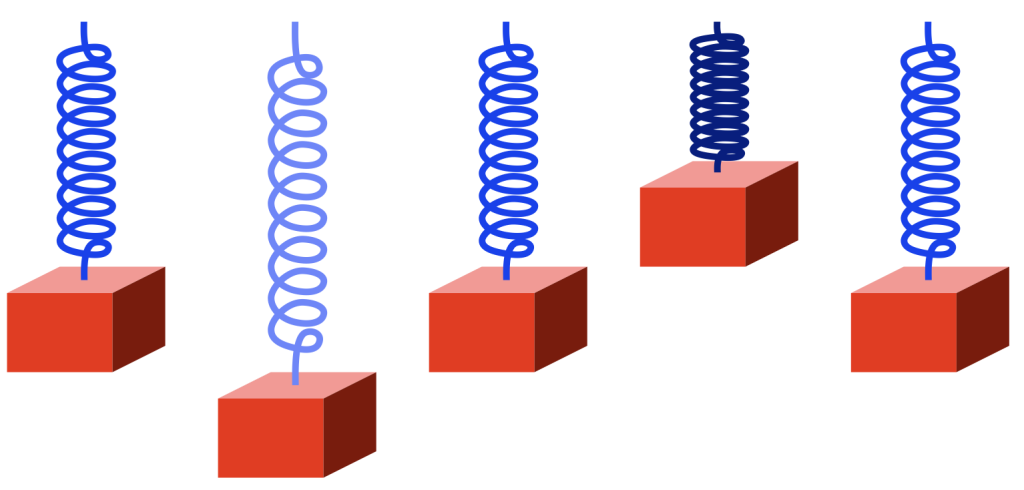
If there were no friction, no air around the block, and no friction within the metal molecules of the spring, then this would bounce up and down forever.
However, there is friction, so some of the movement (“kinetic energy”) is turned into heat and lost. So, each bounce gets smaller and smaller and the maximum velocity of the block (as it passes the resting position) gets lower and lower, until, eventually, it stops moving (at the resting position, where it started).
Notice that I changed the colour of the spring to show when it’s more stretched (lighter blue) and when it’s more compressed (darker blue).
If everything were behaving perfectly, then the RATE at which the bounce repeats wouldn’t change. Only its amplitude (or the excursion of the block, or the height of the bounce) would reduce over time. That bounce rate (let’s say 1 bounce per second, and by “bounce” I mean a full cycle of moment down, up, and back down to where it started again) is the frequency of the repetition (or oscillation).
If you make the weight lighter, then it will bounce faster (because the spring can pull the weight more “easily”). If you make the spring stiffer, then it will bounce faster (because the spring can pull the weight more “easily”). So, we can change the frequency of the oscillation by changing the weight of the block or the stiffness of the spring.
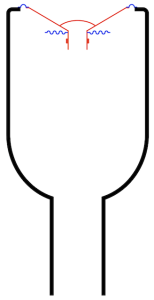
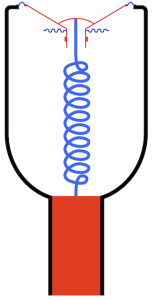
Now take a look at the same weight on a spring next to an up-side down wine bottle that (sadly) has been emptied of wine.

Notice that I’ve added some colours to the air inside the bottle. The air in the bottle itself is blue, just like the colour of the spring. This is because, if we pull air out of the bottle (downwards), the air inside it will pull back (upwards; just like the metal spring pulling back upwards on the block). I’ve made the small cylinder of air in the neck of the bottle red, just like the block. This is because that air has some mass, and it’s free to move upwards (into the bottle) and downwards (out of the bottle) just like the block.
If I were somehow able to pull the “plug” of air out of the neck of the bottle, the air inside would try to pull it back in. If I then “let go”, the plug would move inwards, go too far (because it also has inertia), squeezing (or compressing) the air inside the bottle, which would then push the plug back out. This is shown in the figure below.
At the level we’re dealing with, this behaviour is practically identical to the behaviour of the block on the spring. In other words, although the block and the plug are made of different materials, and although the metal spring and the air inside the bottle are different materials, Figures 3 and 5 show the same behaviour of the same kind of system.
How do you pull the plug of air out of the bottle? It’s probably easier to start by pushing it inwards instead, by blowing across the top.
When you do this, a little air leaks into the opening, pushing the plug inwards. The “spring” in the bottle then pushes the plug outwards, and your cycle has started. If you wanted to do the same thing with the block, you’d lift it and let go to start the oscillation.
However, you don’t need to blow across the bottle to make it oscillate. You can just tap it with the palm of your hand, for example. Or, if you put the bottle next to your ear and listen carefully, you’ll hear a note “singing along” with the sound in the room. This is because the air in the bottle resonates; it moves back and forth very easily at the frequency that’s determined by the mass of the air in the neck and the volume of air in of the bottle (the spring).
However, remember that friction can make the oscillation decay (or die away) faster, by turning the movement into heat.
There’s another way to get either the block or the wine bottle oscillating:
You can move the TOP of the spring (for example, if you pull it up, then the spring will pull the block upwards, and it’ll start bouncing). Or, you could tap the bottom of the wine bottle (which is on the top in my drawings).
This method of starting the oscillation will come in handy in part 2.
I thought that I was finished talking about (and even thinking about) the RCA Dynagroove Dynamic Styli Correlator as well as tracking and tracing distortion… and then I got an email about the last two postings pointing out that I didn’t mention two-channel stereo vinyl, and whether there was something to think about there.
My first reaction was: “There’s nothing interesting about that. It’s just two channels with the same problem, and since (at least in a hypothetical world) the two axes of movement of the needle are orthogonal, then it doesn’t matter. It’ll be the same problem in both channels. End of discussion.”
Then I took the dog out for a walk, and, as often happens when I’m walking the dog, I re-think thoughts and come home with the opposite opinion.
So, by the time I got home, I realised that there actually is something interesting about that after all.
Starting with Emil Berliner, record discs (original lacquer, then vinyl) have been cut so that the “mono” signal (when the two channels are identical) causes the needle to move laterally instead of vertically. This was originally (ostensibly) to isolate the needle’s movement from vibrations caused by footsteps (the reality is that it was probably a clever manoeuvring around Edison’s patent).
This meant that, when records started supporting two audio channels, a lateral movement was necessary to keep things backwards-compatible.
What does THIS mean? It means that, when the two channels have the same signal (say, on the lead vocal of a pop tune, for example) when the groove of the left wall goes up, the groove of the right wall goes down by the same amount. That causes the needle to move sideways, as shown below in Figure 1.

What are the implications of this on tracing distortion? Remember from the previous posting that the error in the movement of the needle is different on a positive slope (where the needle is moving upwards) than a negative slope (downwards). This can be seen in a one-channel representation in Figure 2.
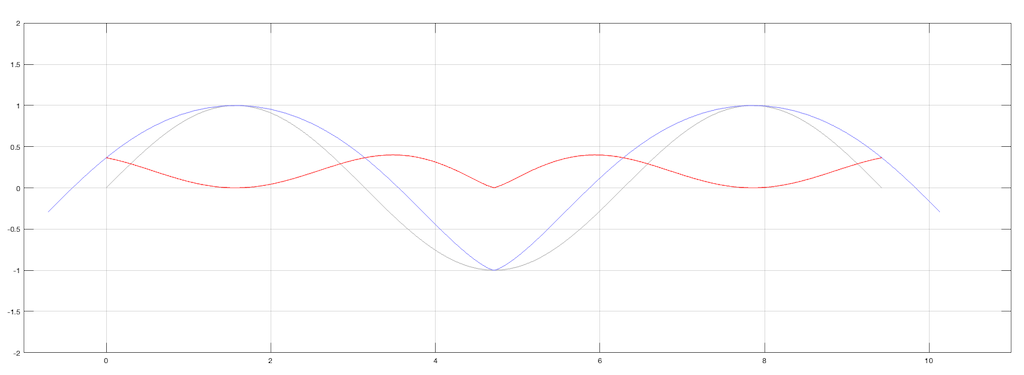
Since the two groove walls have an opposite polarity when the audio signals are the same, then the resulting movement of the two channels with the same magnitude of error will look like Figure 3.
Notice that, because the two groove walls are moving in opposite polarity (in other words, one is going up while the other is going down) this causes the two error signals to shift by 1/2 of a period.
However, Figure 3 doesn’t show the audio’s electrical signals. It shows the physical movement of the needle. In order to show the audio signals, we have to flip the polarity of one of the two channels (which, in a real pickup would be done electrically). That means that the audio signals will look like Figure 4.

Notice in Figure 4 that the original signals are identical (that’s why it looks like there’s only one sine wave) but their actual outputs are different because their error components are different.
But here’s the cool thing:
One way to think of the actual output signals is to consider each one as the sum of the original signal and the error signal. Since (for a mono signal like a lead vocal) their original signals are identical, then, if you sit in the right place with a properly configured pair of loudspeakers (or a decent pair of headphones) then you’ll hear that part of the signal as a phantom image in the middle. However, since the error signals are NOT correlated, they will not be localised in the middle with the voice. They’ll move to the sides. They’re not negatively correlated, so they won’t sound “phase-y” but they’re not correlated either, so they won’t be in the same place as the original signal.
So, although the distortion exists (albeit not NEARLY on the scale that I’ve drawn here…) it could be argued that the problem is attenuated by the fact that you’ll localise it in a different place than the signal.
Of course, if the signal is only in one channel (like Aretha Franklin’s backup singers in “Chain of Fools” for example) then this localisation difference will not help. Sorry.
When you look at the datasheet of an audio device, you may see a specification that states its “signal to noise ratio” or “SNR”. Or, you may see the “dynamic range” or “DNR” (or “DR”) lists as well, or instead.
These days, even in the world of “professional audio” (whatever that means), these two things are similar enough to be confused or at least confusing, but that’s because modern audio devices don’t behave like their ancestors. So, if we look back 30 years ago and earlier, then these two terms were obviously different, and therefore independently usable. So, in order to sort this out, let’s take a look at the difference in old audio gear and the new stuff.
Let’s start with two of basic concepts:
So, the goal of any recording or device that plays a recording is to try and make sure that the audio signal is loud enough relative to that noise that you don’t notice it, but not so loud that the limit is hit.
Now we have to look a little more closely at the details of this…
If we take the example of a piece of modern audio equipment (which probably means that it’s made of transistors doing the work in the analogue domain, and there’s lots of stuff going on in the digital domain) then you have a device that has some level of constant noise (called the “noise floor”) and maximum limit that is at a very specific level. If the level of your audio signal is just a weeee bit (say, 0.1 dB) lower than this limit, then everything is as it should be. But once you hit that limit, you hit it hard – like a brick wall. If you throw your fist at a brick wall and stop your hand 1 mm before hitting it, then you don’t hit it at all. If you don’t stop your hand, the wall will stop it for you.
In older gear, this “brick wall” didn’t exist in lots of gear. Let’s take the sample of analogue magnetic tape. It also has a noise floor, but the maximum limit is “softer”. As the signal gets louder and louder, it starts to reach a point where the top and bottom of the audio waveform get increasingly “squished” or “compressed” instead of chopping off the top and bottom.
I made a 997 Hz sine wave that starts at a very, very low level and increases to a very high level over a period of 10 seconds. Then, I put it through two simulated devices.
Device “A” is a simulation of a modern device (say, an analogue-to-digital converter). It clips the top and bottom of the signal when some level is exceeded.
Device “B” is a simulation of something like the signal that would be recorded to analogue magnetic tape and then played back. Notice that it slowly “eases in” to a clipped signal; but also notice that this starts happening before Device “A” hits its maximum. So, the signal is being changed before it “has to”.

Let’s zoom in on those two plots at two different times in the ramp in level.

Device “A” is the two plots on the top at around 8.2 seconds and about 9.5 seconds from the previous figure. Device “B” is the bottom two plots, zooming in on the same two moments in time (and therefore input levels).
Notice that when the signal is low enough, both devices have (roughly) the same behaviour. They both output a sine wave. However, when the signal is higher, one device just chops off the top and bottom of the sine wave whereas the other device merely changes its shape.
Now let’s think of this in terms of the signals’ levels in relationship to the levels of the noise floors of the devices and the distortion artefacts that are generated by the change in the signals when they get too loud.
If we measure the output level of a device when the signal level is very, very low, all we’ll see is the level of the inherent noise floor of the device itself. Then, as the signal level increases, it comes up above the noise floor, and the output level is the same as the level of the signal. Then, as the signal’s level gets too high, it will start to distort and we’ll see an increase in the level of the distortion artefacts.
If we plot this as a ratio of the signal’s level (which is increasing over time) to the combined level of the distortion and noise artefacts for the two devices, it will look like this:
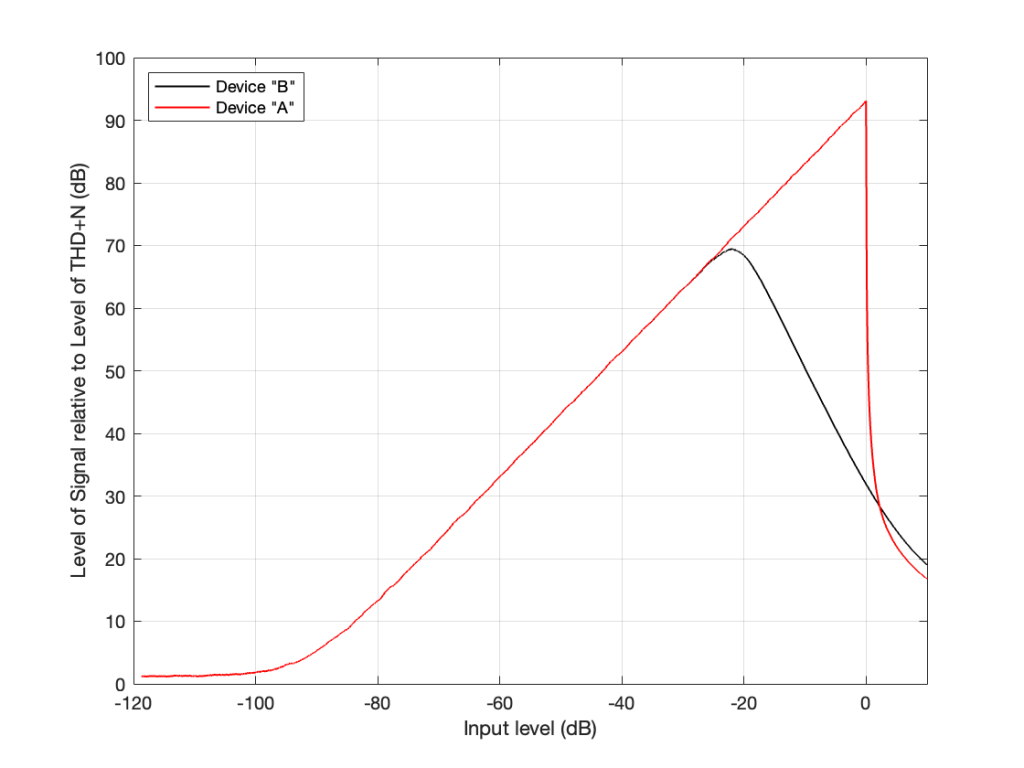
On the left side of this plot, the two lines (the black door Device “A” and the red for Device “B”) are horizontal. This is because we’re just seeing the noise floor of the devices. No matter how much lower in level the signals were, the output level would always be the same. (If this were a real, correct Signal-to-THD+N ratio, then it would actually show negative values, because the signal would be quieter than the noise. It would really only be 0 dB when the level of the noise was the same as the signal’s level.)
Then, moving to the right, the levels of the signals come above the noise floor, and we see the two lines increasing in level.
Then, just under a signal level of about -20 dB, we see that the level of the signal relative to the artefacts starts in Device “B” reaches a peak, and then starts heading downwards. This is because as the signal level gets higher and higher, the distortion artefacts increase in level even more.
However, Device “A” keeps increasing until it hits a level 0 dB, at which point a very small increase in level causes a very big jump in the amount of distortion, so the relative level of the signal drops dramatically (not because the signal gets quieter, but because the distortion artefacts get so loud so quickly).
Now let’s think about how best to use those two devices.
For Device “A” (in red) we want to keep the signal as loud as possible without distorting. So, we try to make sure that we stay as close to that 0 dB level on the X-axis as we can most of the time. (Remember that I’m talking about a technical quality of audio – not necessarily something that sounds good if you’re listening to music.) HOWEVER: we must make sure that we NEVER exceed that level.
However, for Device “B”, we want to keep the signal as close to that peak around -20 dB as much as possible – but if we go over that level, it’s no big deal. We can get away with levels above that – it’s just that the higher we go, the worse it might sound because the distortion is increasing.
Notice that the red line and the black line cross each other just above the 0 dB line on the X-axis. This is where the two devices will have the same level of distortion – but the distortion characteristics will be different, so they won’t necessarily sound the same. But let’s pretend that the the only measure of quality is that Y-axis – so they’re the same at about +2 dB on the X-axis.
Now the question is “What are the dynamic ranges of the two systems?” Another way to ask this question is “How much louder is the loudest signal relative to the quietest possible signal for the two devices?” The answer to this is “a little over 100 dB” for both of them, since the two lines have the same behaviour for low signals and they cross each other when the signal is about 100 dB above this (looking at the X-axis, this is the distance between where the two lines are horizontal on the left, and where they cross each other on the right). Of course, I’m over-simplifying, but for the purposes of this discussion, it’s good enough.
The second question is “What are the signal-to-noise ratios of the two systems?” Another way to ask THIS question is “How much louder is the average signal relative to the quietest possible signal for the two devices?” The answer to this question is two different numbers.
The problem is, these days, a lot of engineers aren’t old enough to remember the days when things behaved like Device “B”, so they interchange Signal to Noise and Dynamic Range all willy-nilly. Given the way we use audio devices today, that’s okay, except when it isn’t.
For example, if you’re trying to connect a turntable (which plays vinyl records that are mastered to behave more like Device “B”) to a digital audio system, then the makers of those two systems and the recordings you play might not agree on how loud things should be. However, in theory, that’s the problem of the manufacturers, not the customers. In reality, it becomes the problem of the customers when they switch from playing a record to playing a digital audio stream, since these two worlds treat levels differently, and there’s no right answer to the problem. As a result, you might need to adjust your volume when you switch sources.
Last week, I was doing a lecture about the basics of audio and I happened to mention one of the rules of thumb that we use in loudspeaker development:
If you have a single loudspeaker driver and you want to keep the same Sound Pressure Level (or output level) as you change the frequency, then if you go down one octave, you need to increase the excursion of the driver 4 times.
One of the people attending the presentation asked “why?” which is a really good question, and as I was answering it, I realised that it could be that many people don’t know this.
Let’s take this step-by-step and keep things simple. We’ll assume for this posting that a loudspeaker driver is a circular piston that moves in and out of a sealed cabinet. It is perfectly flat, and we’ll pretend that it really acts like a piston (so there’s no rubber or foam surround that’s stretching back and forth to make us argue about changes in the diameter of the circle). Also, we’ll assume that the face of the loudspeaker cabinet is infinite to get rid of diffraction. Finally, we’ll say that the space in front of the driver is infinite and has no reflective surfaces in it, so the waveform just radiates from the front of the driver outwards forever. Simple!
Then, we’ll push and pull the loudspeaker driver in and out using electrical current from a power amplifier that is connected to a sine wave generator. So, the driver moves in and out of the “box” with a sinusoidal motion. This can be graphed like this:
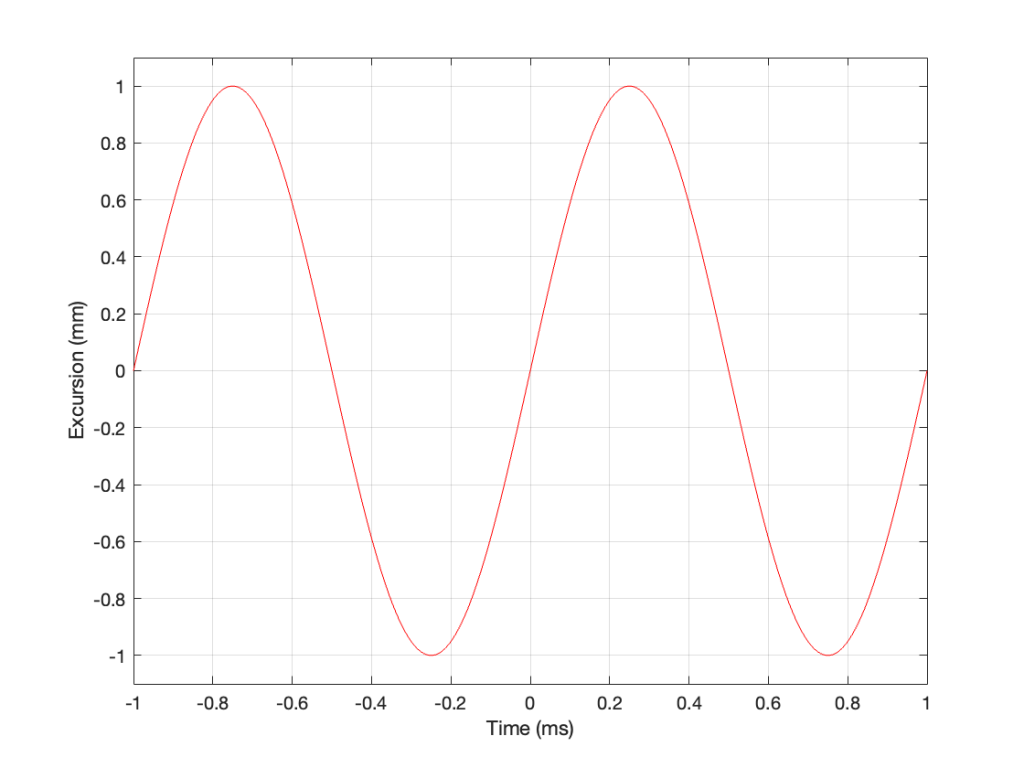
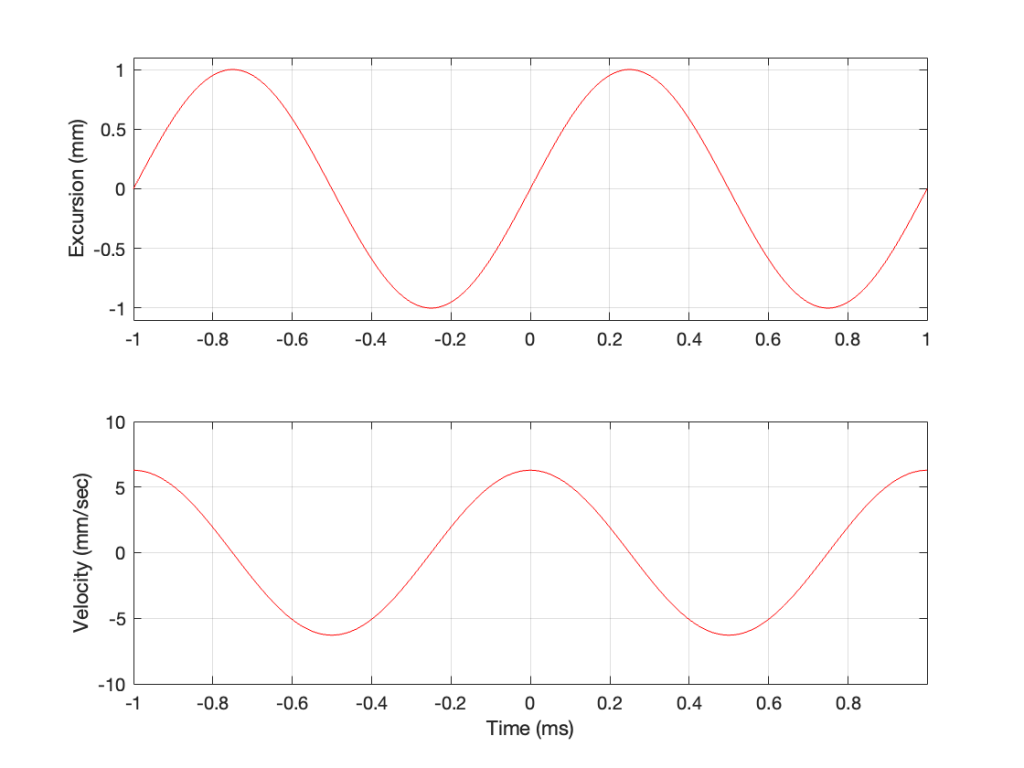
As you can see there, we have one cycle per millisecond, therefore 1000 cycles per second (or 1 kHz), and the driver has a peak excursion of 1 mm. It moves to a maximum of 1 mm out of the box, and 1 mm into the box.
Consider the wave at Time = 0. The driver is passing the 0 mm line, going as fast as it can moving outwards until it gets to 1 mm (at Time = 0.25 ms) by which time it has slowed down and stopped, and then starts moving back in towards the box.
So, the velocity of the driver is the slope of the line in Figure 1, as shown in Figure 2.
As the loudspeaker driver moves in and out of the box, it’s pushing and pulling the air molecules in front of it. Since we’ve over-simplified our system, we can think of the air molecules that are getting pushed and pulled as the cylinder of air that is outlined by the face of the moving piston. In other words, its a “can” of air with the same diameter as the loudspeaker driver, and the same height as the peak-to-peak excursion of the driver (in this case, 2 mm, since it moves 1 mm inwards and 1 mm outwards).
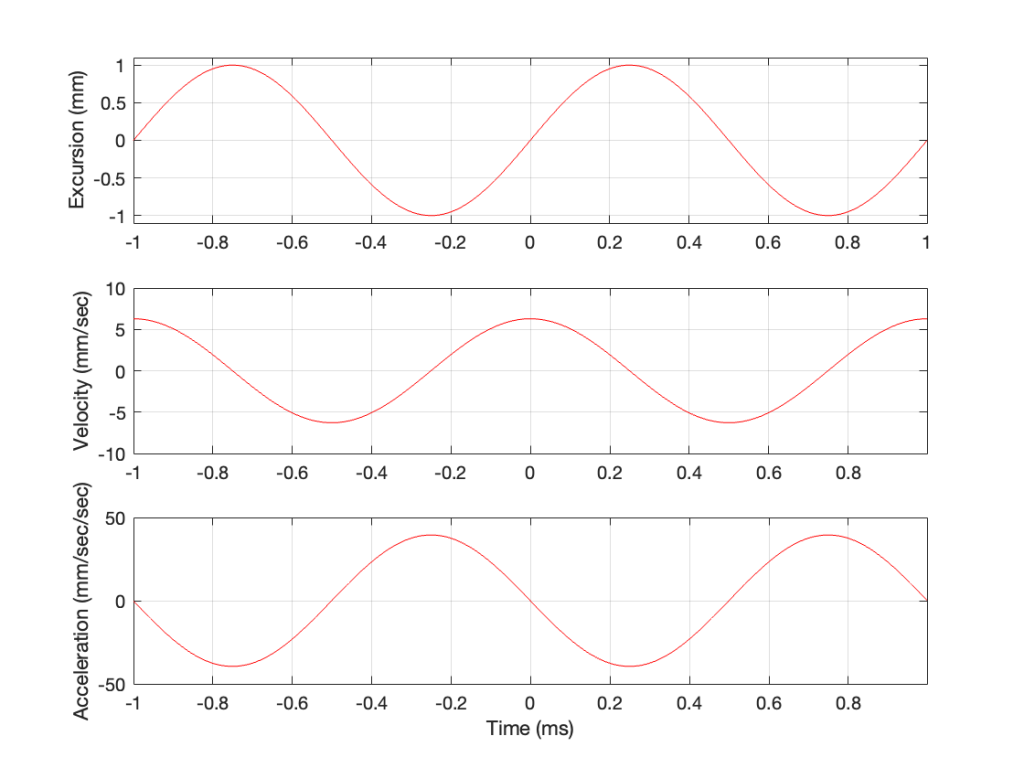
However, sound pressure (which is how loud sounds are) is a measurement of how much the air molecules are compressed and decompressed by the movement of the driver. This is proportional to the acceleration of the driver (neither the velocity nor the excursion, directly…). Luckily, however, we can calculate the driver’s acceleration from the velocity curve. If you look at the bottom plot in Figure 2, you can see that, leading up to Time = 0, the velocity has increased to a maximum (so the acceleration was positive). At Time = 0, the velocity is starting to drop (because the excursion is on its was up to where it will stop at maximum excursion at time = 0.25 ms).
In other words, the acceleration is the slope of the velocity curve, the line in the bottom plot in Figure 2. If we plot this, it looks like Figure 3.
Now we have something useful. Since the bottom plot in Figure 3 shows us the acceleration of the driver, then it can be used to compare to a different frequency. For example, if we get the same driver to play a signal that has half of the frequency, and the same excursion, what happens?
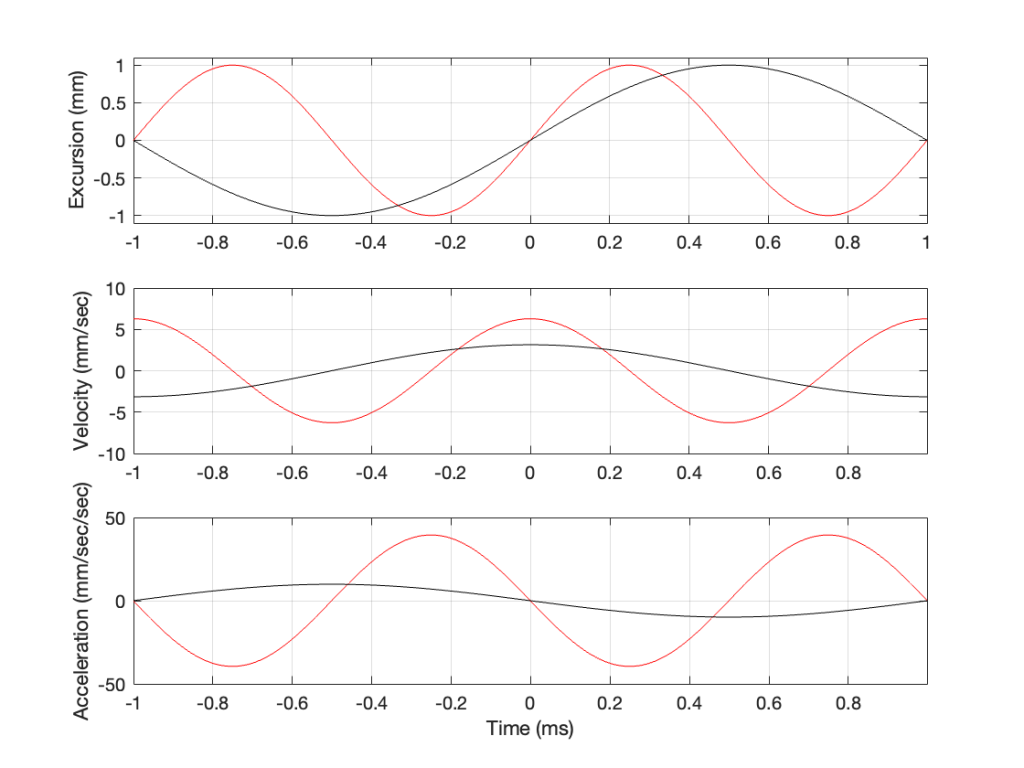
In Figure 4, two sine waves are shown: the black line is 1/2 of the frequency of the red line, but they both have the same excursion. If you take a look at where both lines cross the Time = 0 point, then you can see that the slopes are different: the red line is steeper than the black. This is why the peak of the red line in the velocity curve is higher, since this is the same thing. Since the maximum slope of the red line in the middle plot is higher than the maximum slope of the black line, then its acceleration must be higher, which is what we see in the bottom plot.
Since the sound pressure level is proportional to the acceleration of the driver, then we can see in the top and bottom plots in Figure 4 that, if we halve the frequency (go down one octave) but maintain the same excursion, then the acceleration drops to 25% of the previous amount, and therefore, so does the sound pressure level (20*log10(0.25) = -12 dB, which is another way to express the drop in level…)
This raises the question: “how much do we have to increase the excursion to maintain the acceleration (and therefore the sound pressure level)?” The answer is in the “25%” in the previous paragraph. Since maintaining the same excursion and multiplying the frequency by 0.5 resulted in multiplying the acceleration by 0.25, we’ll have to increase the excursion by 4 to maintain the same acceleration.
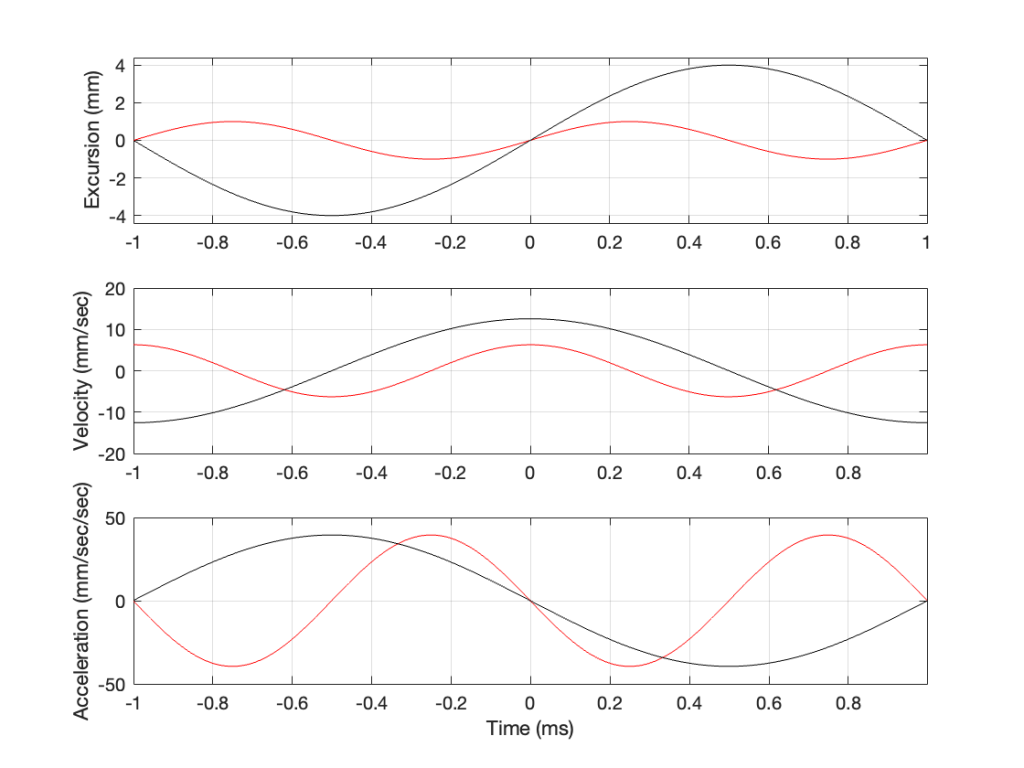
Looking at Figure 5: The black line is 1/2 the frequency of the red line. Their accelerations (the bottom plots) have the same peak values (which means that they produce the same sound pressure level). This, means that the slopes of their velocities are the same at their maxima, which, in turn, means that the peak velocity of the black line (the lower frequency) is higher. Since the peak velocity of the black line is higher (by a factor of 2) then the slope of the excursion plot is also twice as steep, which means that the peak of the excursion of the black line is 4x that of the red line. All of that is explained again in Figure 6.
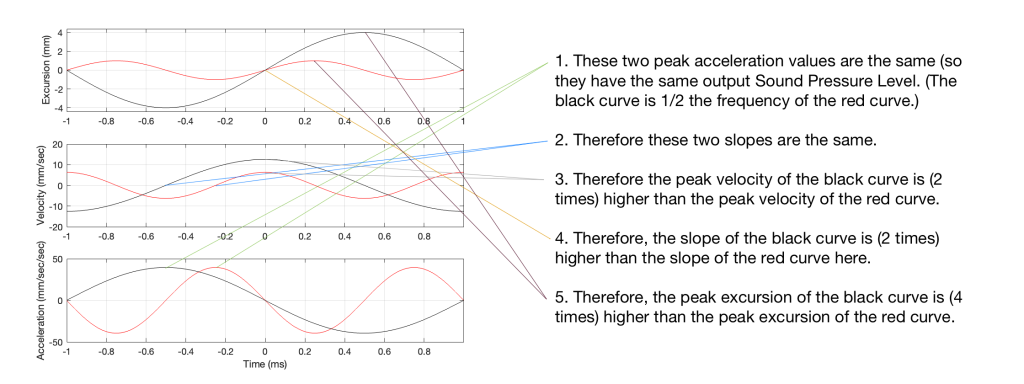
Therefore, assuming that we’re using the same loudspeaker driver, we have to increase the excursion by a factor of 4 when we drop the frequency by a factor of 2, in order to maintain a constant sound pressure level.
However, we can play a little trick… what we’re really doing here is increasing the volume of our “cylinder” of air by a factor of 4. Since we don’t change the size of the driver, we have to move it 4 times farther.
However, the volume of a cylinder is
π r2 * height
and we’re just playing with the “height” in that equation. A different way would be to use a different driver with a bigger surface area to play the lower frequency. For example, if we multiply the radius of the driver by 2, and we don’t change the excursion (the “height” of the cylinder) then the total volume increases by a factor of 4 (because the radius is squared in the equation, and 2*2 = 4).
Another way to think of this: if our loudspeaker driver was a square instead of a circle, we could either move it in and out 4 times farther OR we would make the width and the length of the square each twice as big to get the a cube with the same volume. That “r2” in the equation above is basically just the “width * length” of a circle…
This is why woofers are bigger than tweeters. In a hypothetical world, a tweeter can play the same low frequencies as a woofer – but it would have to move REALLY far in and out to do it.