Category: acoustics
B&O Tech: The Cube
#51 in a series of articles about the technology behind Bang & Olufsen loudspeakers

Sometimes, we have journalists visiting Bang & Olufsen in Struer to see our facilities. Of course, any visit to Struer means a visit to The Cube – our room where we do almost all of the measurements of the acoustical behaviour of our loudspeaker prototypes. Different people ask different questions about that room – but there are two that come up again and again:
- Why is the room so big?
- Why isn’t it an anechoic chamber?
Of course, the level of detail of the answer is different for different groups of people (technical journalists from audio magazines get a different level of answer than lifestyle journalists from interior design magazines). In this article, I’ll give an even more thorough answer than the one the geeks get. :-)
Introduction #1 – What do we want?
Our goal, when we measure a loudspeaker, is to find out something about its behaviour in the absence of a room. If we measured the loudspeaker in a “real” room, the measurement would be “infected” by the characteristics of the room itself. Since everyone’s room is different, we need to remove that part of the equation and try to measure how the loudspeaker would behave without any walls, ceiling or floor to disturb it.
So, this means (conceptually, at least) that we want to measure the loudspeaker when it’s floating in space.
Introduction #2 – What kind of measurements do we do?
Basically, the measurements that we perform on a loudspeaker can be boiled down into four types:
- on-axis frequency response
- off-axis frequency responses
- directivity
- power response
Luckily, if you’re just a wee bit clever (and we think that we are…), all four of these measurements can be done using the same basic underlying technique.
The very basic idea of doing any audio measurement is that you have some thing whose characteristics you’re trying to measure – the problem is that this thing is usually a link in a chain of things – but you’re only really interested in that one link. In our case, the things in the audio chain are electrical (like the DAC, microphone preamplifier, and ADC) and acoustical (like the measurement microphone and the room itself).
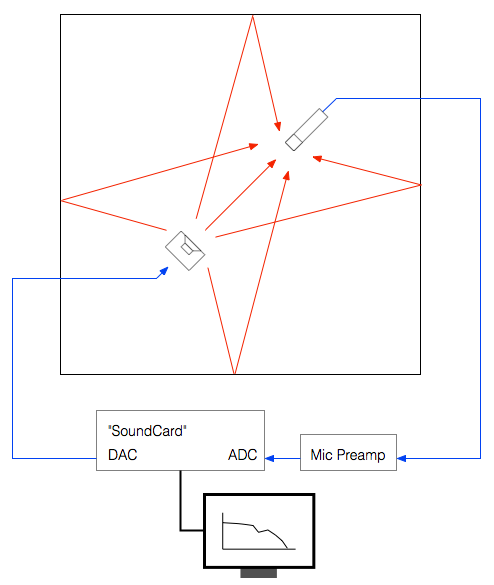
The computer sends a special signal (we’ll come back to that…) out of its “sound card” to the input of the loudspeaker. The sound comes out of the loudspeaker and comes into the microphone (however, so do all the reflections from the walls, ceiling and floor of the Cube). The output of the microphone gets amplified by a preamplifier and sent back into the computer. The computer then “looks at” the difference between the signal that it sent out and the signal that came back in. Since we already know the characteristics of the sound card, the microphone and the mic preamp, then the only thing remaining that caused the output and input signals to be different is the loudspeaker.
Introduction #3 – The signal
There are lots of different ways to measure an audio device. One particularly useful way is to analyse how it behaves when you send it a signal called an “impulse” – a click. The nice thing about a theoretically perfect click is that it contains all frequencies at the same amplitude and with a known phase relationship. If you send the impulse through a device that has an “imperfect” frequency response, then the click changes its shape. By doing some analysis using some 200-year old mathematical tricks (called “Fourier analysis“), we can convert the shape of the impulse into a plot of the magnitude and phase responses of the device.
So, we measure the way the device (in our case, a loudspeaker) responds to an impulse – in other words, its “impulse response”.
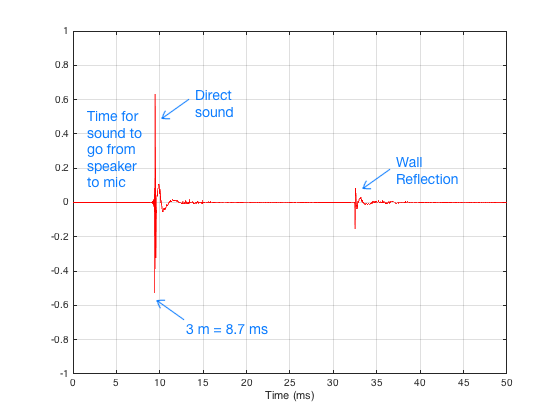
There are three things to initially notice in this figure.
- The first is the time before the first impulse comes in. This is the time it takes the sound to travel from the loudspeaker to the microphone. Since we normally make measurements at a distance of 3 m, this is about 8.7 ms.
- The second is the fact that the impulse doesn’t look perfect. That’s because it isn’t – the loudspeaker has made it different.
- The third is the presence of the wall reflection. (In real life, we see 6 of these – 4 walls, a ceiling and the floor – but this example is a simulation that I created, just to show the concept.)
In order to get a measurement of the loudspeaker in the absence of a room, we have to get rid of those reflections… In this case, all we have to do is to tell the computer to “stop listening” before that reflection arrives. The result is the impulse response of the loudspeaker in the absence of any reflections – which is exactly what we want.
- We make this measurement “on-axis” (usually directly in front of the loudspeaker, at some specific height which may or may not be the same height as the tweeter) to get a basic idea to begin with.
- We can then rotate the crane (the device hanging from the ceiling that the loudspeaker is resting on) with a precision of 1º. This allows us to make an off-axis measurement at any horizontal angle.
- In order to find the loudspeaker’s directivity (like Figure 5, 6, and 7 in this posting), we start by making a series of measurements (typically, every 5º for all 360º around the loudspeaker). We then tell the computer to compare the difference between each off-axis measurement and the on-axis measurement (because we’re only interested in how the sound changes with rotation – not its actual response at a given off-axis angle – we already got that in the previous measurement.
- Finally, we have to get the power response. This one is a little more tricky. The power response is the behaviour of the loudspeaker when measured in all directions simultaneously. Think of this as putting the loudspeaker in the centre of a sphere with a diameter of 3 m made of microphones. We send a signal out of the loudspeaker and measure the response at all points on the sphere, add them all together and see what the total is. This is an expensive way to do this measurement, since microphones cost a lot… An easier way is to use one microphone and rotate the loudspeaker (both horizontally and vertically) and do a LOT of off-axis measurements – not just rotating around the loudspeaker, but also going above and below it. We do each of these measurements individually, and then add the results to get a 3D sum of all responses in all directions. That total is the power response of the loudspeaker – a measurement of the total energy the loudspeaker radiates into the room.


The original questions…
Great. That’s a list of the basic measurements that come out of The Cube. However, I still have’t directly answered the original questions…
Let’s take the second question first: “Why isn’t The Cube an anechoic chamber?”
This raises the question: “What’s an anechoic chamber?” An anechoic chamber is a room whose walls are designed to be absorptive (typically to sound waves, although there are some chambers that are designed to absorb radio waves – these are for testing antennae instead of loudspeakers). If the walls are perfectly absorptive, then there are no reflections, and the loudspeaker behaves as if there are no walls.
So, this question has already been answered – albeit indirectly. We do an impulse response measurement of the loudspeaker, which is converted to magnitude and phase response measurements. As we saw in Figure 5, the reflections off the walls are easily visible in the impulse response. Since, after the impulse response measurement is done, we can “delete” the reflection (using a process called “windowing”) we end up with an impulse response that has no reflections. This is why we typically say that The Cube is “pseudo-anechoic” – the room is not anechoic, but we can modify the measurements after they’re done to be the same as if it were.
Now to the harder question to answer: “Why is the room so big?”
Let’s say that you have a device (for example, a loudspeaker), and it’s your job to measure its magnitude response. One typical way to do this is to measure its impulse response and to do a DFT (or FFT) on that to arrive at a magnitude response.
Let’s also say that you didn’t do your impulse response measurement in a REAL free field (a space where there are no reflections – the wave is free to keep going forever without hitting anything) – but, instead, that you did your measurement in a real space where there are some reflections. “No problem,” you say “I’ll just window out the reflections” (translation: “I’ll just cut the length of the impulse response so that I slice off the end before the first reflection shows up.”)
This is a common method of making a “pseudo-anechoic” measurement of a loudspeaker. You do the measurement in a space, and then slice off the end of the impulse response before you do an FFT to get a magnitude response.
Generally speaking, this procedure works fairly well… One thing that you have to worry about is a well-known relationship between the length of the impulse response (after you’ve sliced it) and the reliability of your measurement. The shorter the impulse response, the less you can trust the low-frequency result from your FFT. One reason for this is that, when you do an FFT, it uses a “slice” of time to convert the signal into a frequency response. In order to be able to measure a given frequency accurately, the FFT math needs at least one full cycle within the slice of time. Take a look at Figure 6, below.
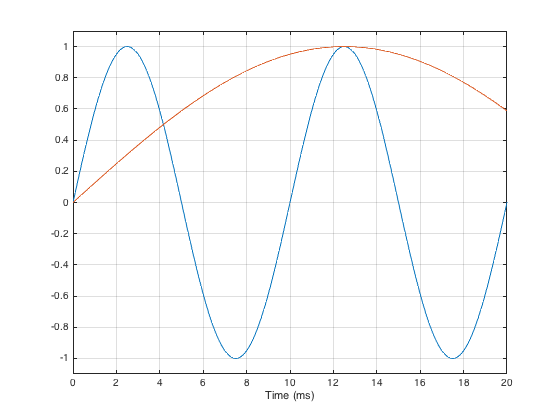
As you can see in that plot, if the slice of time that we’re looking at is 20 ms long, there is enough time to “see” two complete cycles of a 100 Hz sine tone (in blue). However, 20 ms is not long enough to see even one half of a cycle of a 20 Hz sine tone (in red).
However, there is something else to worry about – a less-well-known relationship between the level and extension of the low-frequency content of the device under test and the impulse response length. (Actually, these two issues are basically the same thing – we’re just playing with how low is “low”…)
Let’s start be inventing a loudspeaker that has a perfectly flat on-axis magnitude response but a low-frequency limitation with a roll-off at 10 Hz. I’ve simulated this very unrealistic loudspeaker by building a signal processing flow as shown in Figure 7.
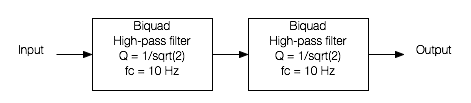
If we were to do an impulse response measurement of that system, it would look like the plot in Figure 8, below.

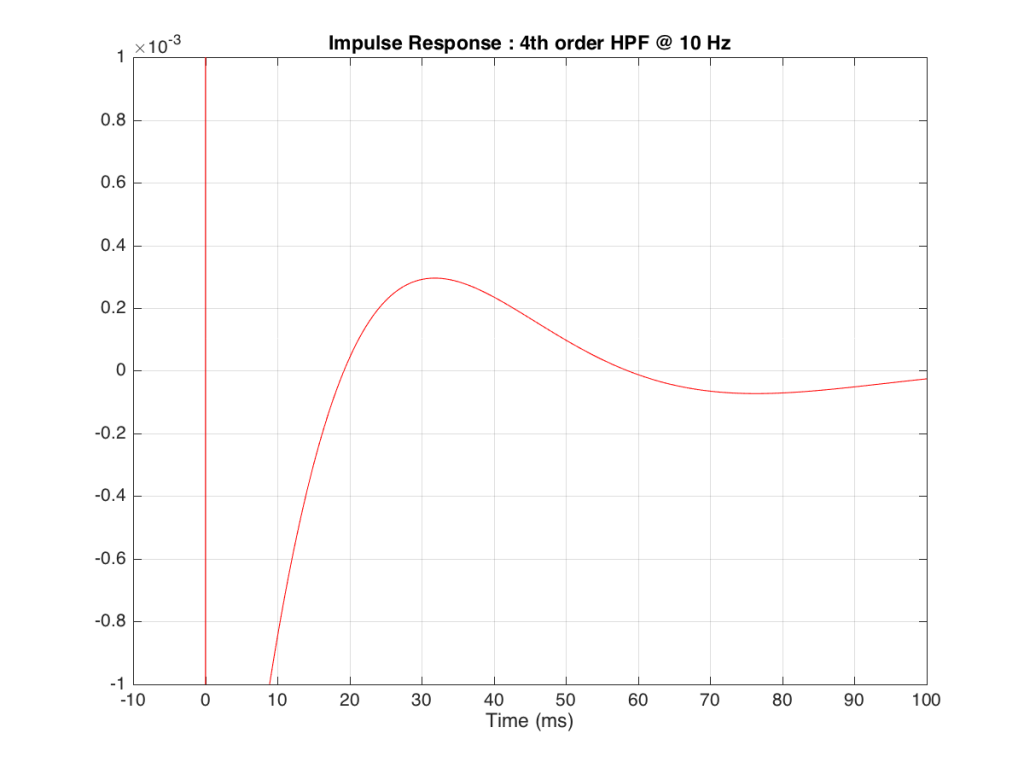
Figure 9, above shows a closeup of what happens just after the impulse. Notice that the signal drops below 0, then swings back up, then negative again. In fact, this keeps happening – the signal goes positive, negative, positive, negative – theoretically for an infinite amount of time – it never stops. (This is why the filters that I used to make this high pass are called “IIR” filters or “Infinite Impulse Response” filters.)
The problem is that this “ringing” in time (to infinity) is very small. However, it’s more easily visible if we plot it on a logarithmic scale, as shown below in Figure 10.
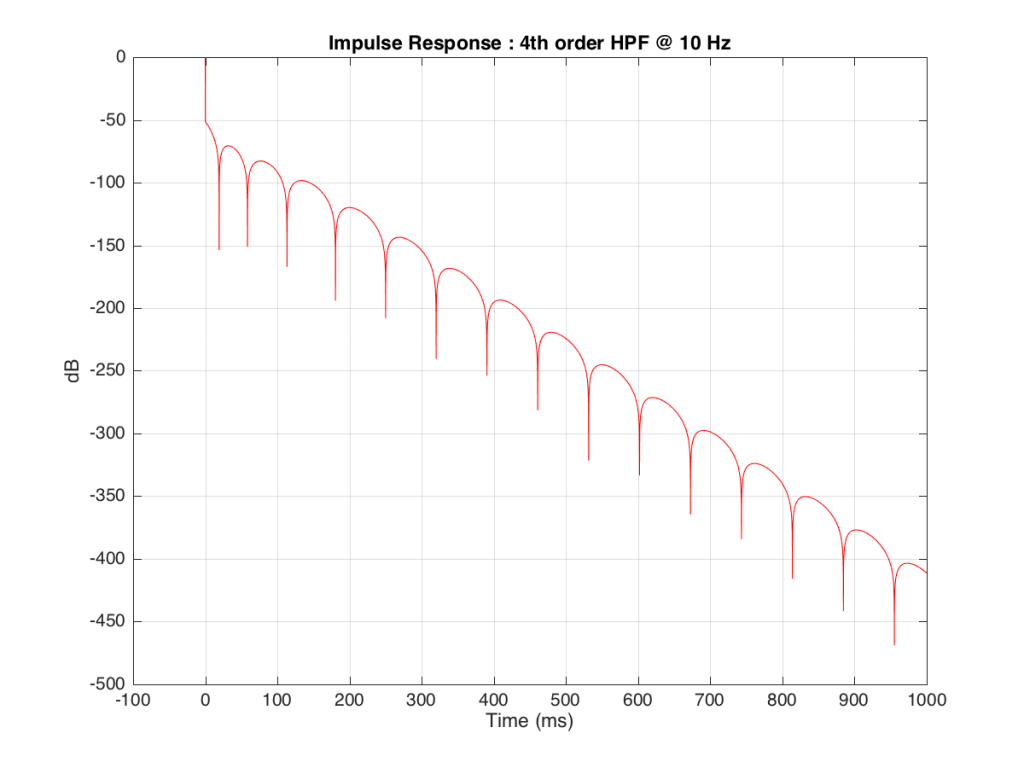
As you can see there, after 1 second (1000 ms) the oscillation caused by the filtering has dropped by about 400 dB relative to the initial impulse (that means it has a level of about 0.000 000 000 000 000 000 01 if the initial impulse has a value of 1). This is very small – but it exists. This means that, if we “cut off” the impulse to measure its frequency response, we’ll be cutting off some of the signal (the oscillation) and therefore getting some error in the conversion to frequency. The question then is: how much error is generated when we shorten the impulse length?
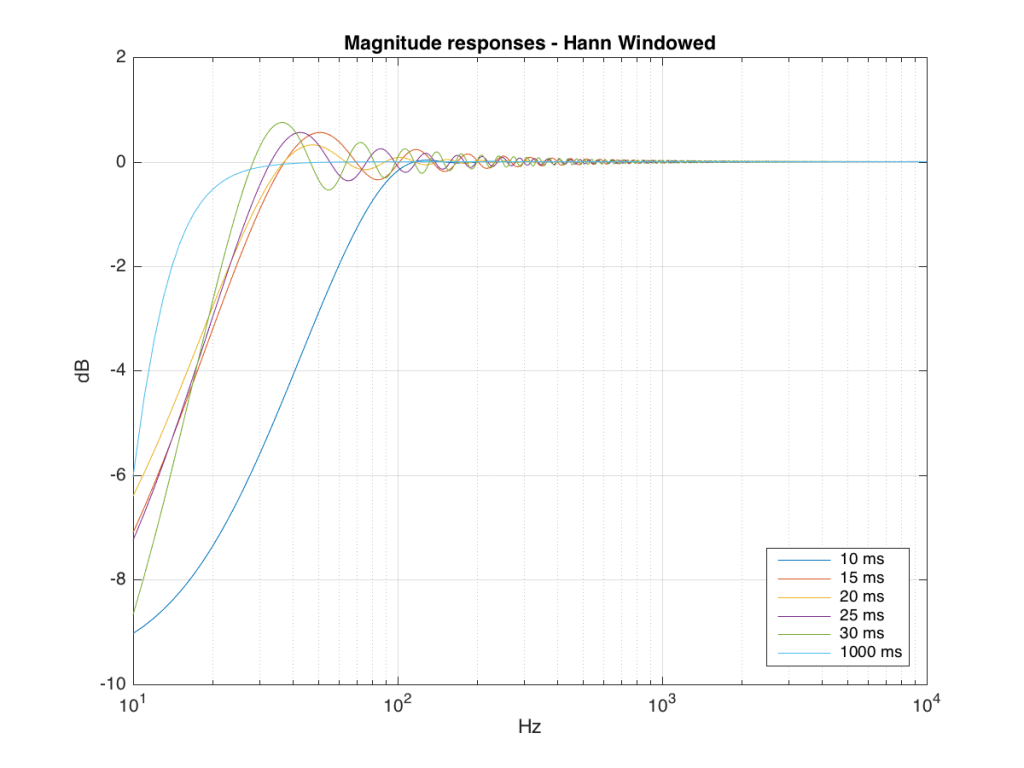
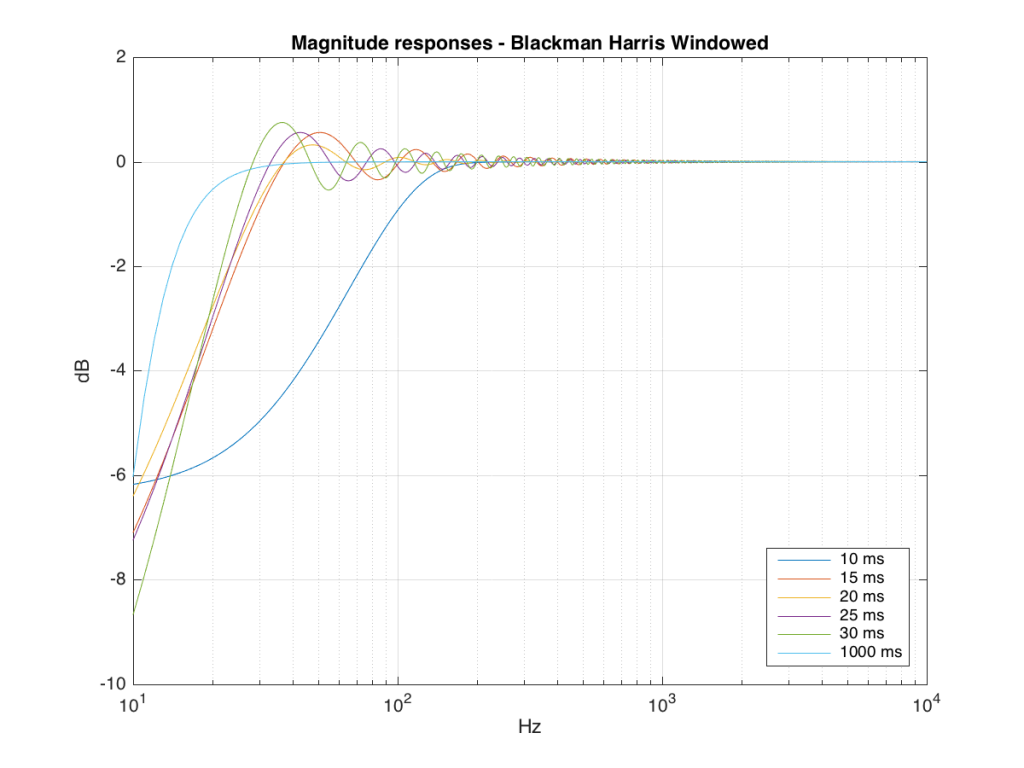
We won’t do an analysis of how to answer this question – I’ll just give some examples. Let’s take the total impulse response shown in Figure 6 and cut it to different lengths – 10, 15, 20, 25, 30 and 1000 ms. For each of those versions, I’ll take an FFT and look at the resulting magnitude response. These are shown below in Figure 11.
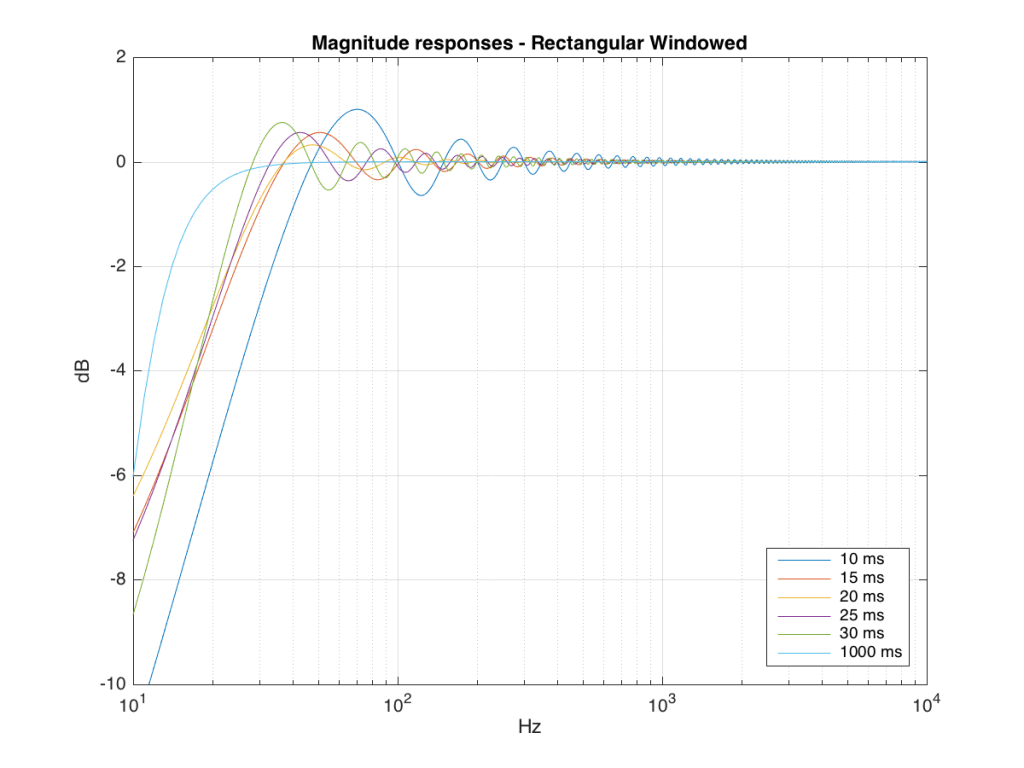
Figure 11: The magnitude responses resulting from taking an FFT of a shortened portion of a single impulse response plotted in Figure 8.
We’ll assume that the light blue curve in Figure 9 is the “reference” since, although it has some error due to the fact that the impulse response is “only” one second long, that error is very small. You can see in the dark blue curve that, by doing an FFT on only the first 10 ms of the total impulse response, we get a strange behaviour in the result. The first is that we’ve lost a lot in the low frequency region (notice that the dark blue curve is below the light blue curve at 10 Hz). We also see a strange bump at about 70 Hz – which is the beginning of a “ripple” in the magnitude response that goes all the way up into the high frequency region.
The amount of error that we get – and the specific details of how wrong it is – are dependent on the length of the portion of the impulse response that we use.
If we plot this as an error – how wrong is each of the curves relative to our reference, the result looks like Figure 12.
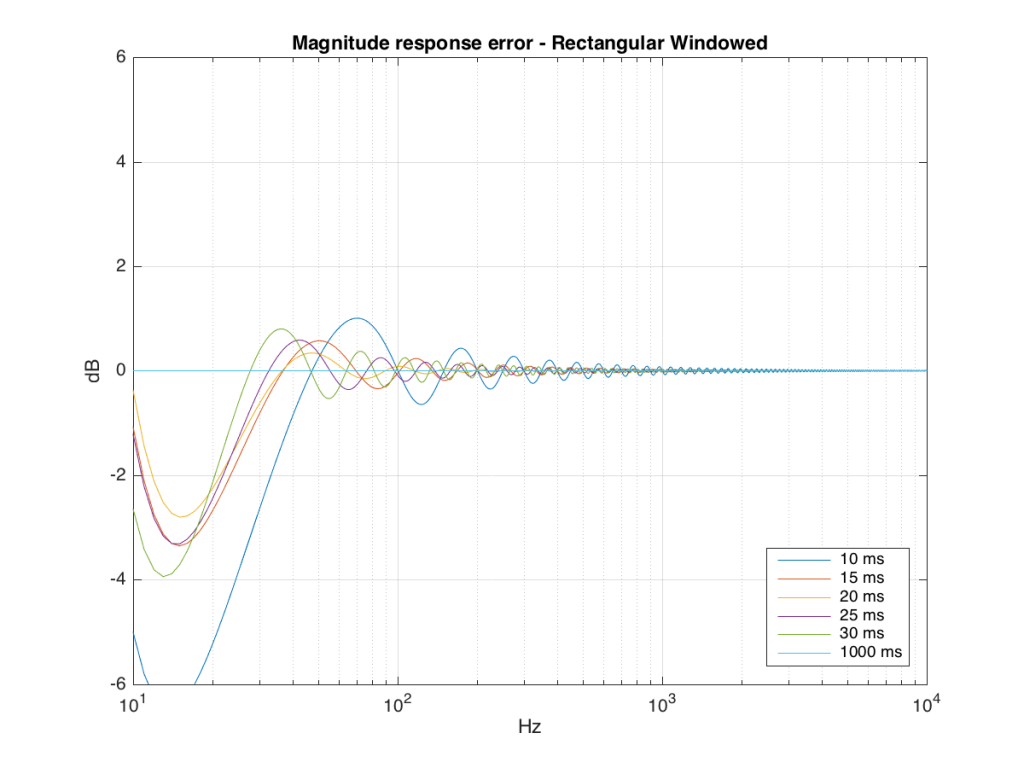
So what?
As you can see there, using a shorted impulse response produces an error in our measurement when the signal has a significant low frequency output. However, as we said above, we shorten the impulse response to delete the early reflections from the walls of The Cube in our measurement to make it “pseudo-anechoic”. This means, therefore, that we must have some error in our measurement. In fact, this is true – we do have some error in our measurement – but the error is smaller than it would have been if the room had been smaller. A bigger room means that we can have a longer impulse response which, in turn, means that we have a more accurate magnitude response measurement.
“So why not use an anechoic chamber and not mess around with this ‘pseudo-anechoic’ stuff?” I hear you cry… This is a good idea, in theory – however, in practice, the problem that we see above is caused by the fact that the loudspeaker has a low-frequency output. Making a room anechoic at a very low frequency (say, 10 Hz) would be very expensive AND it would have to be VERY big (because the absorptive wedges on the walls would have to be VERY deep – a good rule of thumb is that the wedges should be 1/4 of the wavelength of the lowest frequency you’re trying to absorb, and a 10 Hz wave has a wavelength of 34.4 m, so you’d need wedges about 8.6 m deep on all surfaces… This would therefore be a very big room…)
Appendix 1 – Tricks
Of course, there are some tricks that can be played to make the room seem bigger than it is. One trick that we use is to do our low-frequency measurements in the “near field” which is much closer than 3 m from the loudspeaker, as is shown in Figure 13 below. The advantage of doing this is that it makes the direct sound MUCH louder than the wall reflections (in addition to making the difference in their time of arrival at the microphone slightly longer) which reduces their impact on the measurement. The problem with doing near-field measurements is that you are very sensitive to distance – and you typically have to assume that the loudspeaker is radiating omnidirectional – but this is a fairly safe assumption in most cases.

Appendix 2 – Windowing
Those of you with some experience with FFT’s may have heard of something called a windowing function which is just a fact way to slice up the impulse response. Instead of either letting signal through or not, we can choose to “fade out” the impulse response more gradually. This changes the error that we’ll get, but we’ll still get an error, as can be seen below.
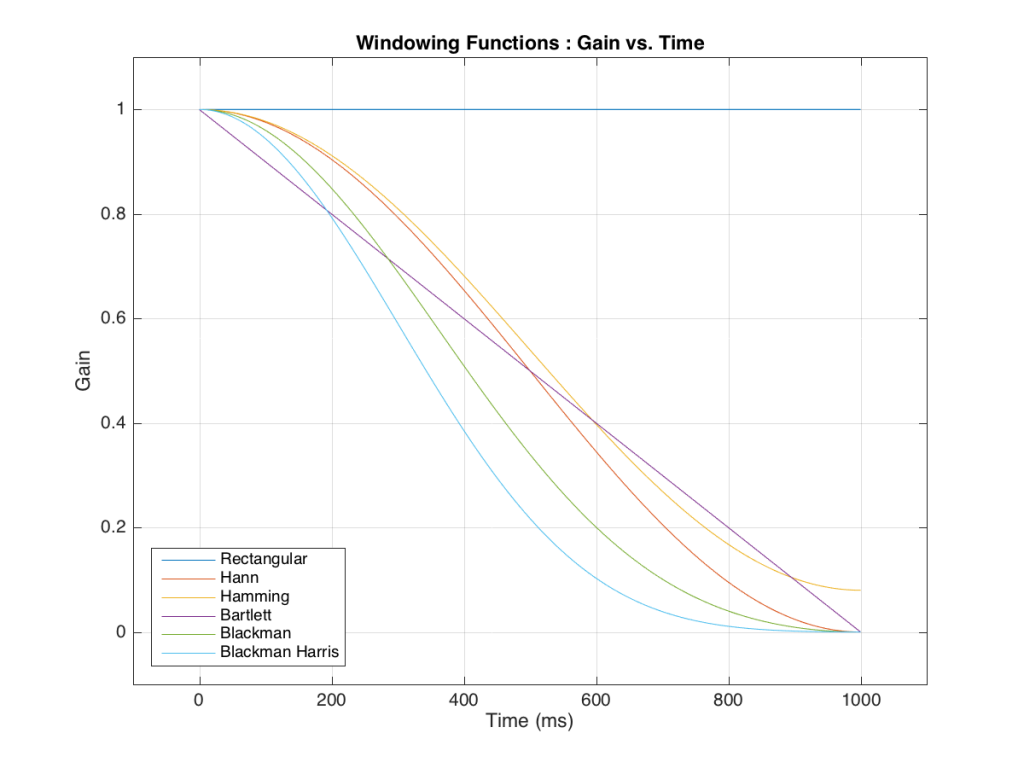
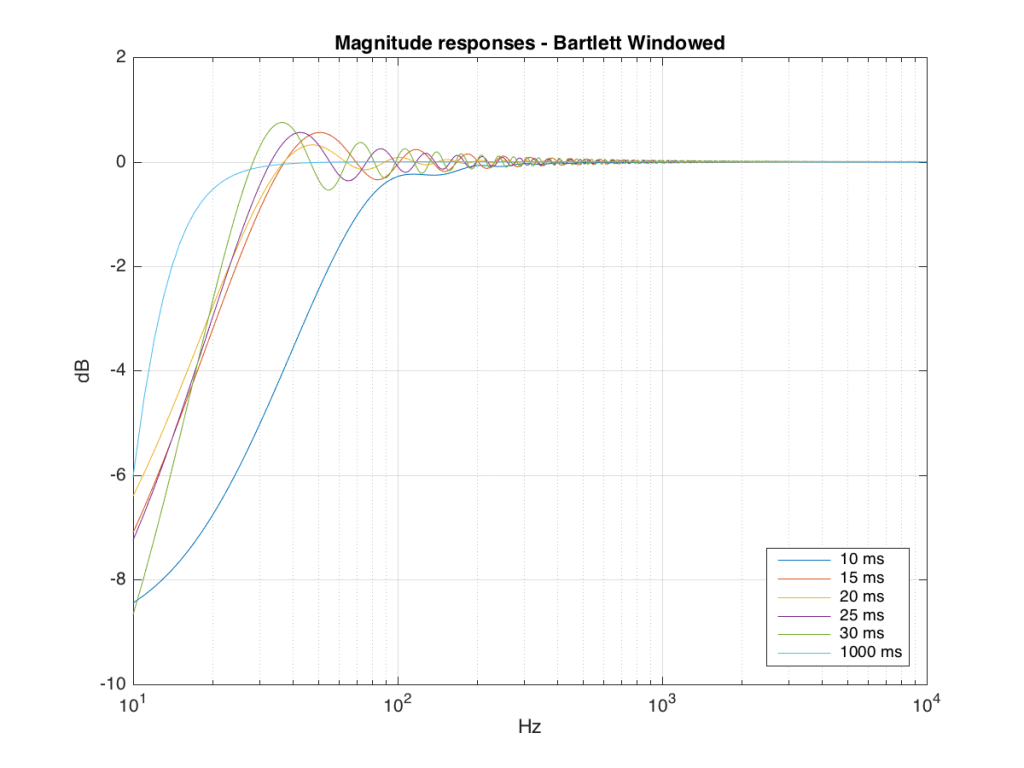
So, as you can see with all of those, the error is different for each windowing function and impulse response length – but there’s no “magic bullet” here that makes the problems go away. If you have a loudspeaker with low-frequency output, then you need a longer impulse response to see what it’s doing, even in the higher frequencies.
“The Power” to shake a building…
B&O Tech: Active Room Compensation – Some More Details, Part 2
#50 in a series of articles about the technology behind Bang & Olufsen loudspeakers
Before we begin, if you’re unfamiliar with the concept of a “room mode”, it might be useful to review three other postings:
But what if my room is Scandinavian?
and
Active Room Compensation – Some Details, Part 1
At the end of that last posting, I said:
“P.S. As I mentioned briefly in this posting, Active Room Compensation has one additional feature – multichannel processing. That will be explained later in Part 2.”
So, that’s the theme for this article – the multichannel aspect of Active Room Compensation.
A monophonic view
Let’s start by looking at Figure 1, below.
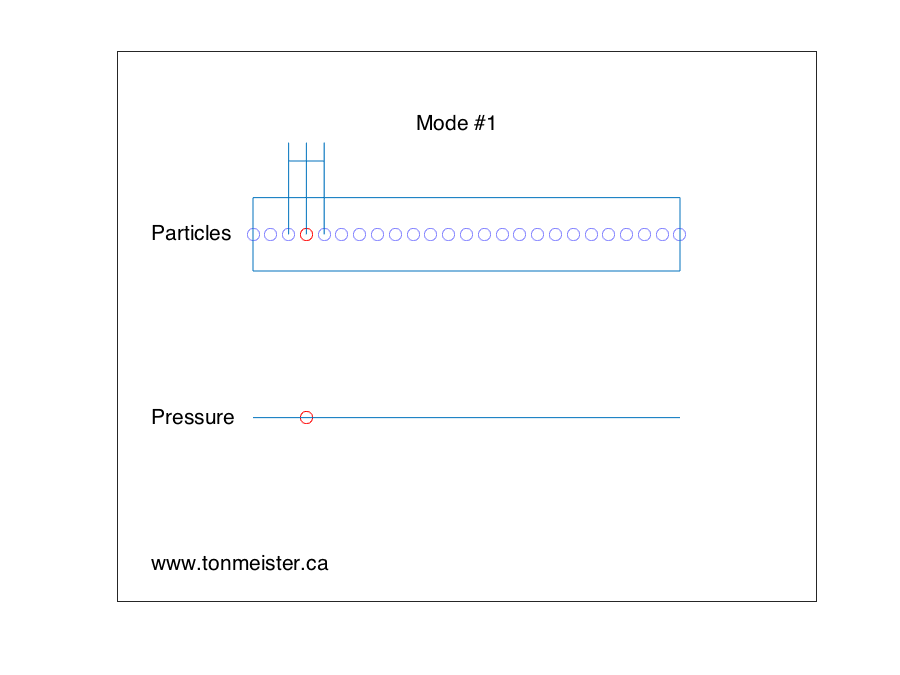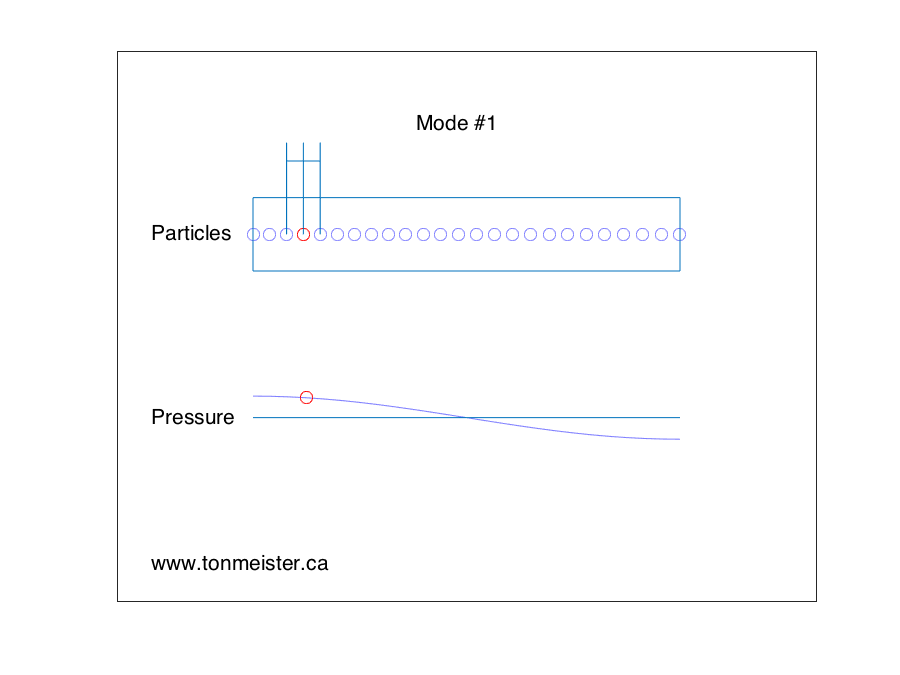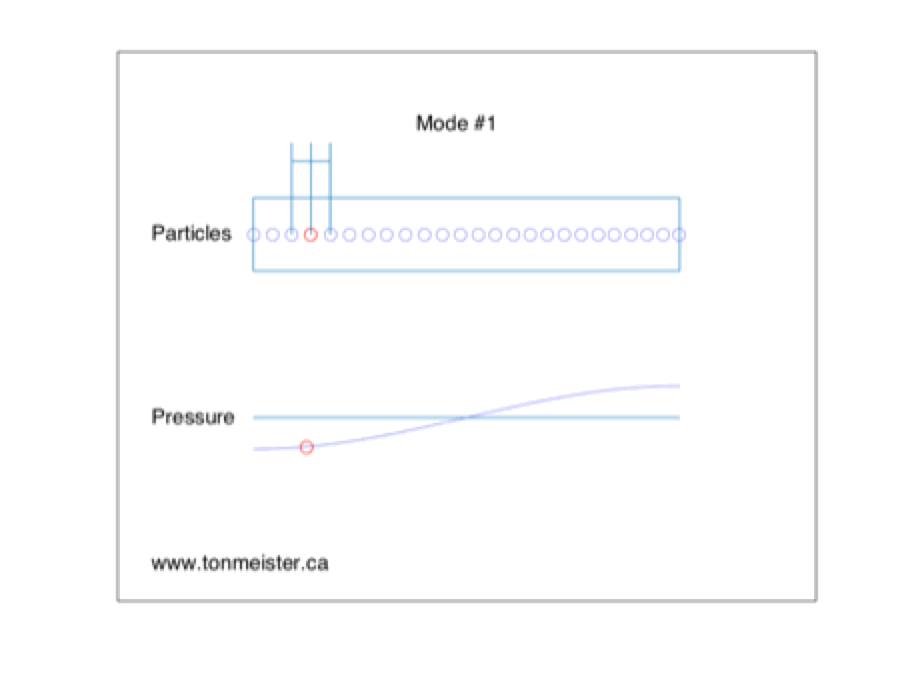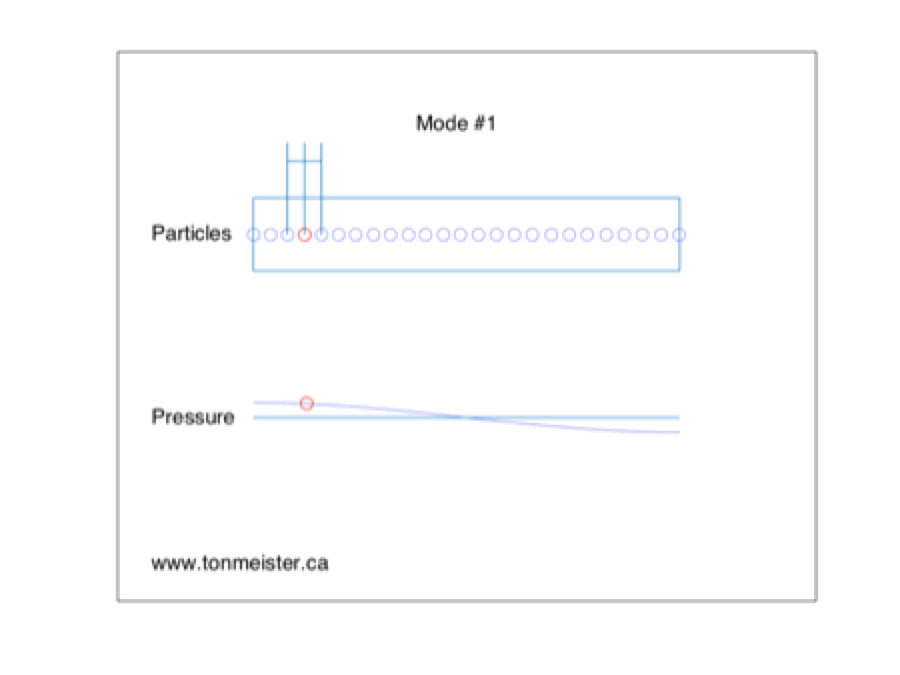
This is a basic representation of the fundamental room mode in one dimension of a room. If a loudspeaker is placed at the location of the red circle and it produces energy at the same frequency of the room mode, then the room will resonate, just like a closed pipe, as can be seen in the animation.
One important thing to notice in the figure above is that when the pressure on one side of the room goes positive, the opposite side goes negative. In other words, the two sides of the room are in opposite polarity. This information will come in handy later.
Now let’s look at the second harmonic – this is a resonance that has a frequency that is two times that of the fundamental mode. Its behaviour in one dimension of the room is shown below. Again, the loudspeaker is in the position of the red circle.
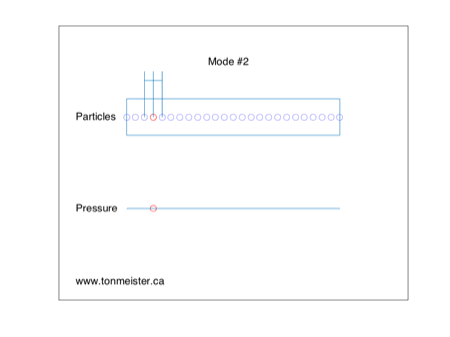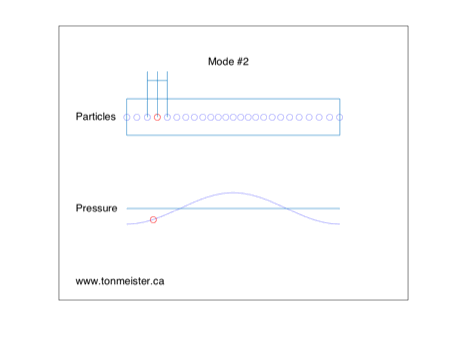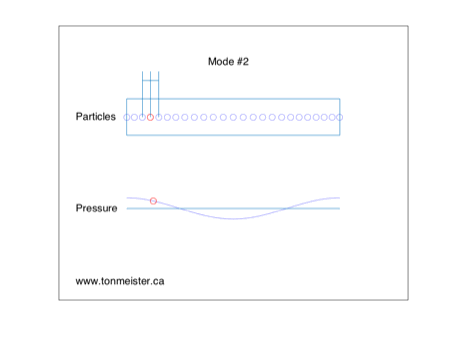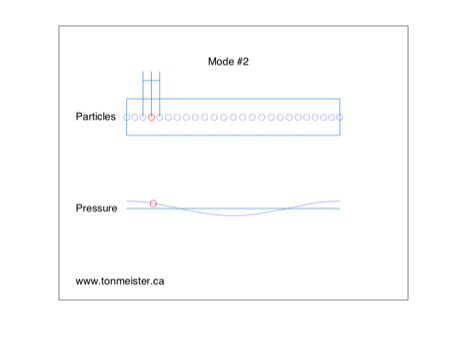
Now, you’ll notice, the two sides of the room have the same polarity – when one goes positive, so does the other. It’s the centre of the room that is in opposite polarity to the sides.
If you measure the natural response of a loudspeaker that is otherwise flat (let’s not split hairs over whether we’re talking about on-axis magnitude response or the power response – for the purposes of this discussion, it’s irrelevant) in a one-dimensional room like the one shown above, you’ll see that there is a natural peak in the response at each frequency where you have a room mode. The result will look something like Figure 3, below
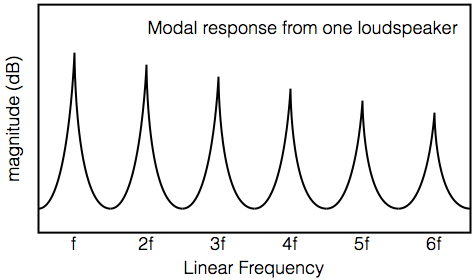
As you can see there, every mode is excited by the loudspeaker (we’re assuming that the loudspeaker is not sitting on a “node” and therefore not coupling to the room mode at all).
So, if you build a room compensation system that only takes one loudspeaker into account, then it will measure a response similar to the one in Figure 3, and it will create a compensation filter that looks something like the one shown in Figure 4.
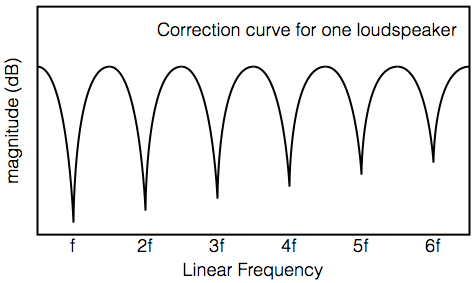
Assuming that you’re careful about your measurements, and you consider things like phase response in your creation of the filter, this system will work very well with just one small problem: most people don’t use only one loudspeaker – they use at least two.
So, how does this change things?
Now, in stereophonic sound*!
Let’s go back and consider our room modes again, this time with two loudspeakers.
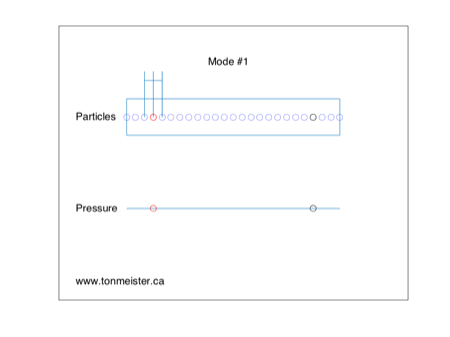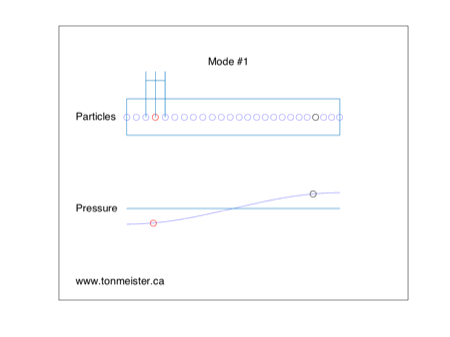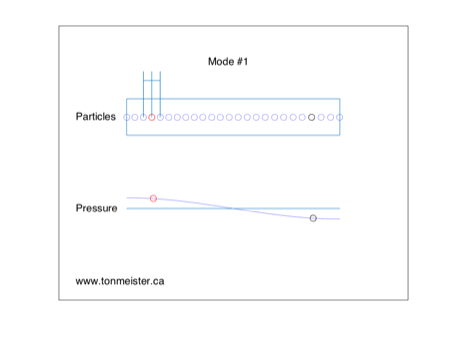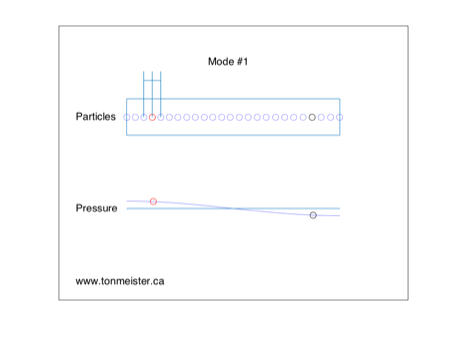
Figure 5, above, shows the same room as in Figure 1, but now I’ve plotted the locations of two loudspeakers, one on the left (atypically, in red) and one on the right (in black). Notice that these two points in the room, when the room mode is ringing, are opposite in polarity (or “out of phase” as many people say…). However, consider that, in most recordings, the bass (which is, in most cases, a good estimation of the frequency band of the fundamental room mode) is panned to the centre, and therefore is “in phase” in the two channels.
In other words, in almost all cases, the two loudspeakers are producing the same signal at the same level, in phase (and therefore with the same polarity). However, the room is ringing in opposite polarity at the two loudspeakers.
What’s the result of this conflict? It’s simple – the room mode is naturally cancelled by the signals in the loudspeakers. In other words, there is no need to apply room correction for a recording like this, with the loudspeakers in the locations that they’re shown in, for this room mode.
So, if you measure each loudspeaker individually, you’ll put a dip in their responses that should not be there to compensate for a room mode that is not ringing. You must consider both loudspeakers playing a correlated signal, and how that will interact with the room mode.
Now let’s look at the next harmonic, shown below in Figure 6.

Now you can see that the mode is ringing in the same phase at the two loudspeaker positions. So, if the bass (still a good guess…) is in phase in the two channels (also a good guess…) then this resonance will be twice as bad as it would be with only one loudspeaker. Again, we need to consider the behaviour of the room mode with a correlated signal in the two loudspeakers – but this time things are worse instead of non-existent.
So, this means that we have to re-consider our room compensation filter. Instead of measuring each loudspeaker independently and building a filter for each one and ignoring that people rarely listen in mono, we have to measure the two (or more) loudspeakers and analyse the way that different signals will interact with the room modes.
For example, in the simple case shown above, we might wind up with the two filters shown in Figure 7 and 8.
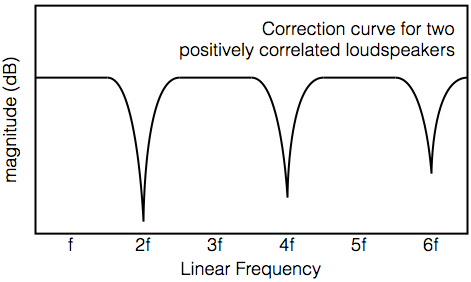
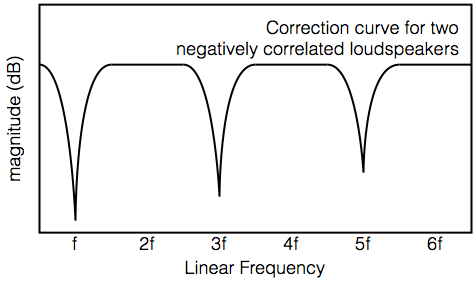
Now, you might be saying “I understand Figure 7 – lots of signals have the same polarity in the two loudspeakers (like the vocals, the bass, the kick drum – anything panned to the centre). But what signals are out-of-phase if I’ve connected by loudspeakers correctly?”
The answer to this comes mainly from classical recordings where it is normal to use microphones (usually omnidirectional) that are spaced apart. In this case, signals enter the two microphones are different times (depending on the angle to the sound source) – and a time difference results in a phase difference.
This processing is done in Beolab 90‘s Active Room Compensation to ensure that the loudspeakers are best optimised, not only to the room they’re in, but their locations within it, and its interaction with the recordings you’re playing. The end result is that each loudspeaker “knows” that the other one is in the room – each not only considers the other’s effect on the room’s response, but they “help each other” to control the room modes.
Of course, I’ve left out a lot of details in this description – for example, the actual responses of the correlated and negatively correlated signals will not really look like the ones I’ve shown here; most rooms contain more than one dimension; and I haven’t talked about boundary effects. In addition, everything I’ve said here is just an example using a very simplified view of the universe. The measurements of the loudspeakers at the microphone positions will result in very different responses than the ones shown here, which will, in turn, result in very different compensation filters.
*Most people don’t seem to know it, but “stereophonic sound” (or “stereo” if you’re into the whole brevity thing) means that you have two or more audio channels. Just thought I’d be explicit here – in case anyone was wondering.
BeoLab 90 reviews
Stereophile
“B&O has also succeeded in using all that technology to serve the music: the BeoLab 90’s sound quality equaled the general performance of any other speaker I’ve heard, and exceeded them in the resolution and stability of the sound-stages the pair of them presented.” (Kal Rubinson)
“For now, I exhort every caring music listener to listen to the BeoLab 90 and hear what is now possible. It’s that good. (KR)
“To say how impressed with how the BeoLab 90 measured in its Narrow mode would be an understatement. This loudspeaker demonstrates just how much can be achieved with intelligent use of DSP to optimise its acoustic performance. As Kal Rubinson summed up, it is a tour de force. Wow! (John Atkinson)
Lyd og Bilde Norway
“Lyden av BeoLab 90 er vanskelig å forklare, den må egentlig bare oppleves. Personlig har jeg aldri hørt en mer livaktig musikkgjengivelse, og flere som har vært på besøk reagerte med å klype seg i armen eller felle en tåre når de hørte et opptak de kjente, eller rettere sagt trodde de kjente!”
“The sound of the BeoLab 90 is hard to explain, it must really be experienced. Personally I have never heard a more lifelike music reproduction, and several who have been visiting reacted by pinching their own arm or shedding a tear when they heard a recording they knew, or rather thought they knew!”
After Munich High End 2016
From fineartofliving.de: “Fazit: Bang & Olufsen BeoLab 90 – Die Zukunft des Klangs? Die Antwort darauf: Nach unserer Meinung zurzeit eine, wenn nicht sogar die beste Möglichkeit für optimales Klangerlebnis im High End-Bereich. Mit einer Einschränkung: Selbst angesichts des nicht minder beachtlichen Preises kann es aufgrund der hohen Nachfrage zu Lieferengpässen kommen…..
From www.hificlube.net: High End 2016 – Munich – Best Sound: Runner-up – “My colleague Martin Colloms wrote a long feature article about the Beolab 90 for Hificritic. Still I wasn’t ready for what I heard. An immersive holographic sound even when I was sitting no more than 5 feet away from the loudspeakers. Excellent focus, amazing localization of musicians and singers in the huge and deep soundstage. Maybe a hint of upper mid emphasis. To say that I am amazed is an understatement. It gets an A verging on the A+…”
Press reviews from CES 2016
soundstagehifi.com: “…this demonstration was, by far, the best I heard – and the BeoLab 90 was my favorite product – at CES 2016.”
stereophile.com: “The sound was incredibly dynamic but relaxed. This was the best bass I heard at the show, and the most startlingly different soundstaging and midrange I experienced during CES 2016.
“The question I’ve been asked at every CES more often than any other is “Which sound system impressed you the most?” It’s a question that’s often difficult to answer. Typically, I’ve been impressed by several systems, often for different reasons, and it’s hard to say which was “the best.” That is, except at CES 2016. This time, I had no trouble answering this question: the BeoLab 90. The sound was utterly natural, effortless, with outstanding soundstage and imaging. I also couldn’t help but be impressed by the technology represented by this speaker system: 18 drivers of the highest quality, 18 amplifiers, full DSP control, cast aluminum enclosure. Given the components and the extensive research that went into the design of the speaker, $75,000 for the pair does not seem excessive.”
digitaltrends.com: “When we sat down for a short audition, we were gobsmacked by what we were hearing. Though we were in the very back of the room with enough people blocking our sight of the speakers that we could barely see the system, we heard a perfectly balanced presentation with the vocals seemingly coming from directly in front of us, just 2 feet away (someone’s head was in that spot).

audio-head.com: “From common audiophile test tracks to a sweet spot rotation, whoever was leading the charge at the company certainly seemed vastly familiar with the hobby’s eccentric standards. The sound of the BEOLAB 90 followed in suit, the quick listening session yielded surprisingly tight image and responsive dynamic range. The bass was big, properly proportioned and beautiful in a way that reminded me of other high end rigs that play in this price range. Overall, it felt like a very impressive presentation that didn’t disappoint, checking off boxes left and right for both the audiophile and the luxury lifestyle listener.”

AVSforum.com: “These speakers have real guts, and yet possess more finesse than passive speakers I’ve heard that cost even more. In the rarefied price point that they occupy, Bang and Olufsen’s flagship speakers actually strike me as a bargain, as outrageous as that may sound when discussing $80,000 speakers. But, that’s exactly how good they are. Respect.”
soundstageglobal.com: “what I heard from the pair at CES 2016 absolutely blew me away — the way the pair imaged, coupled with the fullness, richness, and presence exhibited, had me talking about them for the rest of the day. Now I feel a little foolish for at first thinking they were a stupid design. Don’t make the same mistake — hear a pair of 90s if you can.”
bloomberg.com: “We got a brief demo and the sound is incredible.”
wired.com: “The soundstage is breathtaking, the low end is positively massive. Possibly the best speakers I’ve ever heard. Possibly the very speakers Crom has in his throne room in Valhalla.”
highdefdigest.com: “Having two of these exquisite pieces focused on me made for a smooth, powerful sound that will likely standout in my memory for the rest of my life. For those who can indulge, I strongly advise doing so.”
From the early press events
“So how did the BeoLab 90 make us feel? When we closed our eyes in Bang & Olufsen’s special listening room, the pair of master reference speakers (#2 and #3 ever made)—along with the room—seemed to vanish the instant a song played. We weren’t listening to sound emanating from two specific points; instead, the Weeknd was singing his heart out right in front of us. Benny Goodman’s band performed an intimate set, and you could picture where each musician was sitting. The BeoLab 90’s ability to create such a lifelike three-dimensional sound stage is unparalleled when you’re sitting in the sweet spot. It certainly brings up the question of whether a speaker can be “too” good for the music—some now-classic albums weren’t necessarily well-recorded and mastered (think of when the Rolling Stones turned the basement of a rented French mansion into a makeshift studio slash drug den). But when all the variables align perfectly, the music engulfs listeners entirely and hits the guts. The result of such incredible technology and engineering happens to be a very visceral human experience.”
“Die Abbildung war phänomenal, jedes Instrument der gewählten Musik nahm ganz selbstverständlich den für sich bestimmten Platz im Raum ein, jedes Element war von Anfang bis Ende verfolg- und erlebbar. Aber nicht nur die Ortung verblüffte, auch die Detailgenauigkeit, mit der selbst kleinste Feinheiten bis zum erkälteten Backgroundsänger aufgedeckt wurde, sucht ihresgleichen.”
– modernhifi.de
“Vi kan bevidne, at effekten er besnærende. Højttalerne spiller sammen med lytterummet på en måde, vi ikke har oplevet før. Personligt har jeg aldrig hørt et mere holografisk realistisk lydbillede, hverken i eller uden for sweet spot. BeoLab 90 er også en fuldblods, fullrange-højttaler, der ikke overlader noget til tilfældighederne.”
– lydogbillede.dk
“I found that the size of the soundstage was consistently proportional to the size of the ensemble and the recording. I found that the bass was very well extended, taut, and satisfying. Most of all, I was impressed by the prototypes’ reproduction of detail throughout the audio band, and the uniformity of that quality across the soundstage.”
– Kalman Rubinson, Stereophile magazine (print version, October, 2015)
“Wohl noch nie haben Lautsprecher die musikali schen Akteure so scharf ins Wohnzimmer projiziert. Ganz gleich, ob grosse Orchester oder kleine Jazz-Formationen – jedes ein zelne Instrument hat seinen exakten Platz im virtuellen Raum, der auch seine Tiefen dimension verblüffend genau zu erkennen gibt: Der Hörer kann zum Beispiel fast in Zentimetern abzählen, wie weit das Schlag zeug hinter dem Kontrabass placiert ist. Dass der Beolab 90 auch für schwärzeste BassTiefe, überbordende Dynamik und feinen, luftigen Obertonglanz steht, müssen TestHörer der Vollständigkeit halber natür lich ebenfalls zu Protokoll geben, aber das eigentlich Spektakuläre des Lautsprechers ist tatsächlich seine überragende räumliche Abbildung.”
– NZZ am Sonntag 18. Oktober 2015
For more comments and reviews:
How Bang & Olufsen’s BeoLab 90 Became a Reality: www.coolhunting.com
Skønheden eller udhyret? Bag om B&O BeoLab 90: www.recordere.dk
BeoLab 90: B&O laver banebrydende højttaler: www.lydogbillede.dk
Beolab 90 is Bang & Olufsen’s striking 90th anniversary speaker: www.whathifi.com
Der Traum vom Raum: Frankfurter Allgemeine
Bang & Olufsen BeoLab 90: Erster Hörtest: www.modernhifi.de
Outside the mainstream press…
diyaudio.com: “The Beolab 90 is a BEAST; I’m surprised Bang & Olufsen wasn’t kicked out of CES. I never even got close to the SPL limits of my Summas, but if the Beolab 90 had a limit, I couldn’t tell what it was. B&O cranked it up for a couple of tracks, and you could FEEL the bass. … The sound is clean and dynamic. The soundstage is whatever you give it; give it a good recording and the soundstage is pinpoint and huge, give it a crummy recording and it’s crummy. … If you couldn’t tell yet, this is the best speaker I’ve ever heard, bar none. In fact, I feel a little silly lumping it in with other loudspeakers.”
beoworld.org: I have heard a lot of powerful speakers, veeeery expensive speakers, crazy speakers and well, very much different setups. But the Beolab90 blew my mind! … The power in them, the presence of all the tones, the clarity of the sound, the smoothness, the details…. I could go on for ever. It was like I had smooth whipped butter made out of diamonds inside my ears. I will probably never again, or at least for sure not in a long time hear a speaker like this again. I will surely hear the BL90 again, but I doubt something else will beat this. It could very well be the best speaker ever made. Simple as that. Mind you, that they had only the basic software in them, so they are just getting better.”
Loudspeaker driver excursion vs. voltage
This shows the relationship between the voltage applied to the terminals of a loudspeaker drivers (shown on the oscilloscope) and the excursion of the driver.
The frequency of the sine wave driving the system ranges from 1 Hz to 6 Hz, so we stay below the resonance frequency of the driver.
The jump in level as the frequency is increased is caused by the low frequency roll-off of the DAC that I’m using to send the signal to the amplifier. Its manufacturer wasn’t expecting anyone to use it at 1 Hz…
Loudspeaker Diaphragm Movement
In the last posting I made, I did the typical over-simplification and implied that the movement of a loudspeaker diaphragm is “pistonic” (meaning that the whole diaphragm moves as one solid, stiff structure).
In real life, this is not true. I’ll write more about this in a future posting, but for now, I made an animation to show a couple of examples of an exaggerated real life… There’ll be an explanation of this later.
B&O Tech: Why select one driver over another? (Part 1)
#49 in a series of articles about the technology behind Bang & Olufsen loudspeakers
Once-upon-a-time, I wrote an article in this series about how a loudspeaker driver is made and (to some extent) how it works. Just recently, a reader asked a question related not only to this topic, but specifically to the BeoLab 90. Teddy wrote:
I am very curious as to why a driver like a Scanspeak Illuminator can reproduce so much more detail of the original signal when the fundamental design principles are just like less expensive drivers. I guess my question is how is a driver with superior detail retrieval designed and constructed? Also, what other benefits do you see when working with high end drivers?
I’m not sure that I can answer this question directly – but, in thinking about an answer, I realised that it might be interesting to talk about one reason why one loudspeaker driver is chosen over another in a given application or project.
A quick background sidebar: a moving coil dynamic loudspeaker driver is a device that converts an electrical signal into mechanical movement. A voltage is applied to the terminals which causes current to flow through the voice coil (which is wrapped around a tube called a “former” that is attached to the “diaphragm” or “cone” – see Figures 1, 2, 3, and 4, below). That current generates a magnetic field around the wire – and since the coil is sitting in the magnetic field of a permanent magnetic, it wants to move. Depending on the direction of the current, the voice coil will either push outwards or pull inwards resulting in some excursion of the voice coil, former and diaphragm (those parts are all glued together). The whole thing doesn’t fly off because it’s held back by the loudspeaker’s “suspension”. The suspension is comprised of two things – the “surround” (usually a rubber ring that connects the edge of the diaphragm to the top of the basket – the metal frame that supports the whole assembly) and the “spider” (a ring of stretchy fabric that connects the former to the basket). The reason there are two components to the suspension is to ensure that, when the diaphragm moves in and out, it doesn’t rock from side to side. If you want a more complete version of this story, read this article.



When building any loudspeaker, you have to make some decisions about which driver to use. Lots of factors come into this decision – frequency range, maximum sound pressure level (vs. frequency), directivity (vs. frequency), size, sensitivity, cost, and many more things are weighed in order to make the most appropriate choice for the product. (If you’re making a passive loudspeaker, then the frequency response of the driver is important – but if you’re making an active loudspeaker, particularly one that is DSP-based, this is less of a concern, since it can be fixed (more or less…) in the processing.) One of the more significant issues in this list that an acoustical engineer worries about is the nonlinear distortion characteristics of the driver. (This is a big concern with a DSP-based active loudspeaker because non-linear distortion cannot be fixed in the processing.) If the movement of the driver’s diaphragm isn’t the same shape as the electrical signal that you put into it (for example, if you apply a nice smooth electrical sine wave at the speaker terminals, but the diaphragm moves in a jerky square wave fashion, then the output of the speaker isn’t the same as the input) then the signal has been distorted. There are different types of distortion, so we have to be a little more specific.
Linear distortion is what you have when the change to the signal can be “undone”. For example, if you add bass to a signal, then you’ve distorted it (the output of the bass boost is not the same as the input – but that’s the point). However, if you remove bass from the result, you can (in theory) get back what you started with.
Non-linear distortion is what you have when the change to the signal cannot be undone. If you put in a sine wave and the system clips (“chops off”) the top of it, there’s no way of regaining the nice smooth wave that you started with, because there’s no way of knowing what was there before the signal was chopped off.
Non-linear distortion can be generally broken into two general headings: harmonic distortion (sometimes abbreviated THD for Total Harmonic Distortion) and intermodulation distortion (or IMD). Harmonic distortion happens when you put in a signal with one frequency (say, a sinusoidal wave at 1 kHz) and you get out energy at other frequencies (that are multiples of the frequency of the input signal) as well (say, 2kHz, 3 kHz, 4 kHz, and so on…). Intermodulation distortion occurs when you put in more than one frequency (say, 900 Hz and 1000 Hz simultaneously) and you get out other frequencies that are usually mathematically related to the input (typically the sum and difference of multiples of the input frequencies – so, in our example, 1900 Hz (900+1000), 100 Hz (or 1000-900), 2900 Hz (2*1000+900), 1100 Hz (2*1000-900) and lots more…)
Another sidebar: These differences in distortion means that when you say “the signal sounds distorted” – the statement is about as useful as saying “the signal sounds different”. This is even true if you measure the distortion of a system and specify it with a number. See this posting and this posting for a more thorough discussion of this problem…
Back to our loudspeaker: in an ideal world, a loudspeaker driver’s movement would be an exact “replica” (more like an analogy) of the input signal. Sadly, this is never true. Never.
So, we start by accepting the knowledge that a loudspeaker driver is imperfect – and therefore it will impose some harmonic distortion and some intermodulation distortion on the signal. The next question is “why?” and “how can we minimise it?”
In order to talk about that, let’s take a driver and cut it in half. This is shown in Figure 4.
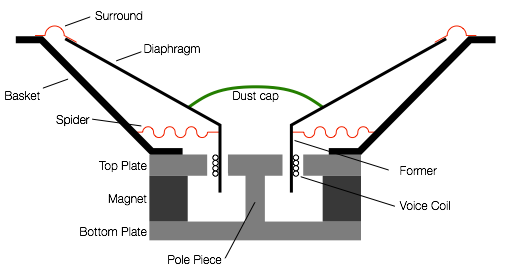
There are some moving parts of the loudspeaker driver. These are the diaphragm and dust cap, the former and the voice coil. these are all glued together and move as one part (hopefully…). When they move, the suspension (the surround and the spider) are stretched in one direction or the other. This can be seen in Figure 5.
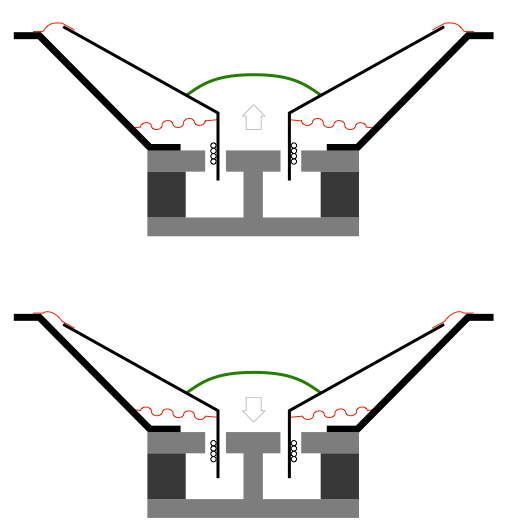
Now, let’s pretend that the movement of the diaphragm (and the dust cap, former, and voice coil) is caused by you (instead of being moved by the voice coil) – you’re the one pushing and pulling the moving parts. When the diaphragm is at the rest position, it’s easy to move. However, as you push it further and further out, it becomes harder and harder to move, since the suspension is stretching more and more. (This is just like an elastic band – stretching it a little bit is easy, stretching it a lot is hard.) If you’re pulling the driver inwards, then it’s the same – the father you get from the rest position (the greater the excursion) the harder it is to move.
This behaviour is called the stiffness of the suspension (although it is also called the compliance – which is how not-stiff it is…). We can measure the suspension stiffness and plot it on a graph, relative to how far away the diaphragm is from the rest position (the excursion). An example of this is shown in Figure 6. (Note that Figure 6 is not the actual measurement of a real driver – I just drew a graph to illustrate the concept.)
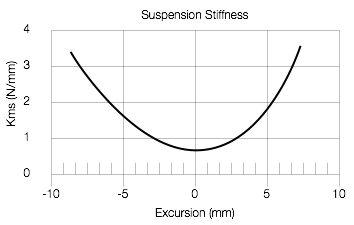
There are two things to notice in the graph in Figure 6. The first is that, as the excursion of the diaphragm moves away from the rest position (either inwards or outwards) the suspension gets stiffer (or harder to move). This means that you need less force to move the diaphragm from 0 mm to 1 mm than you do from 5 mm to 6 mm. the second thing is to notice that the curve is not symmetrical. For example, when the diaphragm has moved outwards by 5 mm, the suspension is stiffer than it is if you move it inwards by 5 mm.
Both of these things will be important later.
Now let’s consider what’s really doing the pushing and pulling. As I described above, when we apply a voltage to the terminals of the voice coil, a current runs through it and it turns into an electromagnet with a magnetic field around it. If the current goes in one direction, one side of the coil is north and the other is south. If we reverse the current direction, we flip the polarity of the electromagnet. The voice coil is already sitting inside the magnetic field of a permanent magnet, so when it gets its own magnetic field it will try to move in one direction or the other, depending on which end is north and which is south (which are dependent on the direction of the current which is dependent on which loudspeaker terminal has the positive voltage and which has the negative.)
The bigger the difference in voltage we apply at the terminals, the greater the current through the voice coil, and the stronger the electromagnet. This means that we will be applying more force to move the voice coil (and the former, the diaphragm, and the dust cap) outwards or inwards.
However, there’s a problem in that last statement. We only have the force to move the voice coil if there’s a magnetic field (from the permanent magnet) to push against. If there were no permanent magnet, there would not be anything for the electromagnet (the voice coil) to push against, so it wouldn’t move.
But look again – closely – at Figures 5 and 6. When the voice coil is at rest, it’s sitting in the “gap” which is where the magnetic field is strongest. However, as it moves inwards or outwards, it also moves out of the gap, and therefore out of the magnetic field. This is illustrated below in the three drawings in Figure 7.

Look at the three drawings in Figure 7 which show that, as the coil moves inwards or outwards, part of the coil moves out of the magnetic field (green arrows), so there’s nothing for it to push against. This means that the bigger the excursion of the diaphragm, the less force with which you have to push (or pull) it. This force factor (abbreviated Bl – but we won’t talk about why…) is a product of the strength of the magnetic field, the length of wire in the coil. That value is multiplied by the amount of current flowing through the coil to find the force delivered by the system. However, as we can see above, is also dependent on the position of the voice coil relative to the gap. that change in force factor can be measured for the driver as a function of its excursion. An example of this is shown in Figure 8, below. (Note that Figure 8 is not the actual measurement of a real driver – I just drew a graph to illustrate the concept.)
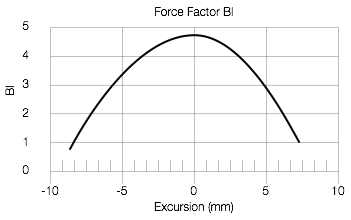
Now, hopefully, you will be asking yourself a very important question. If you look at Figure 6, you can see that, as the excursion of the driver increases, the harder it is to move, so we should have more force factor available to move it. However, Figure 8 shows us that as the excursion of the driver increases we lose force factor… This is something like losing horsepower in your car’s engine every time you go up a hill…
Sadly, although the graphs I drew in Figures 6 and 8 are just invented curves that I drew, they’re not unusual to see… What’s the effect? Basically, it means that you don’t have the ability to push the driver as far out (or in) as you would like, so the peaks (and troughs) in your waveform will be flattened. If either the stiffness or the force factor curves (or both) are asymmetrical, then the flattening will be different on the outwards excursion than the inwards (in other words, the peaks will be squashed differently than the troughs). The total result is that the driver distorts the signals – and you’ll get both harmonic distortion and intermodulation distortion. The less flat the stiffness and/or force factor curves, the more distortion you’ll get. In addition, if you lose force factor with excursion, then when you have an impulsive sound (like a kick drum, for example), you can start moving the diaphragm outwards (because you have force factor at the rest position to do the throwing) but you don’t have the force factor to control its return – so you throw the speaker out, and hope that it comes back instead of pulling it back… This is another form of distortion – but it’s a time-based distortion that might look like “ringing” for example.
But what is it that you want?
In a perfect world, the stiffness of the suspension would be the same, regardless of the excursion of the driver – in other words, it would be a horizontal line instead of the curve in Figure 6. Also, in a perfect world, you would not lose force factor with excursion. In other words, you could always have the same amount of control over the driver, regardless of how far in or out it is.
In order to flatten the stiffness, we have to look at the behaviour of the surround and the spider (if we’re ignoring the effect of the air behind the driver in the loudspeaker enclosure, which, in a real world, cannot be ignored… but let’s stay out of the real world for the purposes of this discussion). One simple method of flattening the stiffness vs. excursion is to make the driver suspension to allow for a much bigger excursion than you expect, for example. If we look at the measured stiffness of the Scan-Speak Illuminator 12MU/4731T00 (the midrange driver in the BeoLab 90), it looks like the graph in Figure 9. (I traced this using the plot in this article.)

There are two things to notice about this stiffness curve. The first is how flat it is around the rest position. The second is that it’s very symmetrical, particularly around the rest position. (This is the reason the mirror image of the stiffness curve is plotted (in grey) – so that you can see the symmetry of the curve.) So, one reason we chose the Scanspeak Illuminator midrange for the Beolab 90 was for this stiffness curve. The “so what?” of this is that the distortion of the driver is lower than with a typical driver.
Next, we look at the force factor or Bl curve. The Illuminator midrange has an unusually flat Bl curve, as can be seen in Figure 10 (also copied from the pdf file lined above). Looking at Figures 9 and 10 together, you can see that, if you stay within an excursion of ± 5 mm or so, both the stiffness and the Bl curves are flat – so the distortion imposed on the audio signal by the driver is very low. Of course, we push the driver further than 5 mm, but even then, the two curves show us that the driver “behaves” better than most…

How is such a flat Bl curve achieved? Take a look at Figure 11, below.
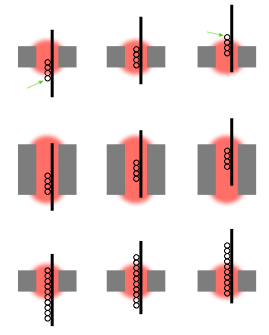
The top three drawings in Figure 11 show the same situation as was shown in Figure 7. As you can see there, as the voice coil moves, it moves out of the magnetic field and we lose force. However, look at the middle three drawings. In this case, the magnetic field (in red) is much bigger than the coil. So, even though the coil moves inwards and outwards, none of it leaves the magnetic field. This is called an “underhung” design – and the result is a flattened Bl curve. We don’t lose force factor because the coil is always in the gap and therefore doesn’t see a change in the magnetic field.
Another way to achieve the same effect is to make the voice coil much bigger than the magnetic field – an “overhung” design. So, the same amount of it is always in the gap.
There are advantages and disadvantages to each of these options. In an underhung design, you have a big magnet, and therefore the driver is heavy – so it’s not typically seen in automotive loudspeakers. The overhung design has a heavy voice coil which is harder to move, so you don’t usually see it in drivers for higher-frequency applications… However, if your ONLY concern is the Bl curve, either design will improve your performance.
The Scanspeak Illuminator uses the underhung design, which is is not hard to figure out just by looking at the photos of it in Figures 12 and 13.


Wrapping up
The stiffness and Bl curves of the Illuminator midrange and the resulting low distortion are just one aspect of the driver that contributed to its choice for the Beolab 90. As I said at the start of the article, there are many, many factors that have to be considered when choosing a driver for a loudspeaker. It is also important to remember that a driver that is a good choice for one loudspeaker does not necessarily mean that it’s a good choice for another loudspeaker. A gearbox that’s perfect for a racing motorcycle is not necessarily going to work well on an 18-wheeler truck. A racing bicycle can go fast partly due to its tires – however, if you put the same tires on a Ferrari, you won’t get very far… Every individual component of any loudspeaker has to be chosen with all of the other components in mind to build an optimal system.
B&O Tech: Intuitive Directivity Plots v.2
#48 in a series of articles about the technology behind Bang & Olufsen loudspeakers
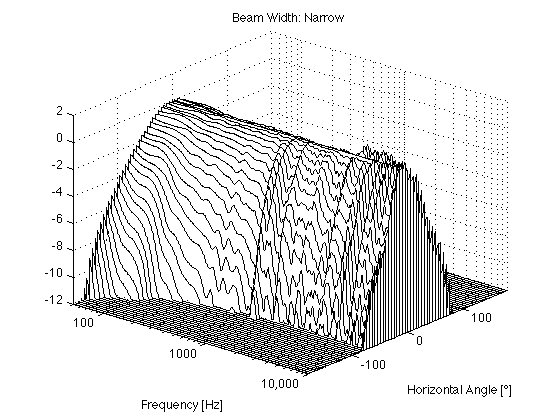
In a past article, I tried to come up with an intuitive way of representing the beam width (or “directivity” – if you’re a geek) of the BeoLab 90. I realised after posting, that there is another way to do this which is used in loudspeaker reviews in some magazines (mostly because it’s the way directivity is plotted by MLSSA). So, I’ve taken the same data as before, and re-plotted it using a “waterfall” function in Matlab. It’s just a different way of looking at the same information – but it might be helpful.
If you’re curious about the details regarding the data itself, this is described here.


B&O Tech: Intuitive Directivity Plots
#46 in a series of articles about the technology behind Bang & Olufsen loudspeakers
I’ve been writing and presenting a lot of information over the past couple of months about the general topic of loudspeaker directivity or “Beam Width” as we call it in the BeoLab 90. One thing that I’ve noticed is that, every time I have to do this in person, I have to explain how to read our directivity plots. This has made me realise that these are not necessarily intuitive to someone that doesn’t look at these kinds of plots (or topographic maps) every day. So, I’ve been working on finding different ways to show the same data. This posting is a first attempt – there will probably be others in the future…
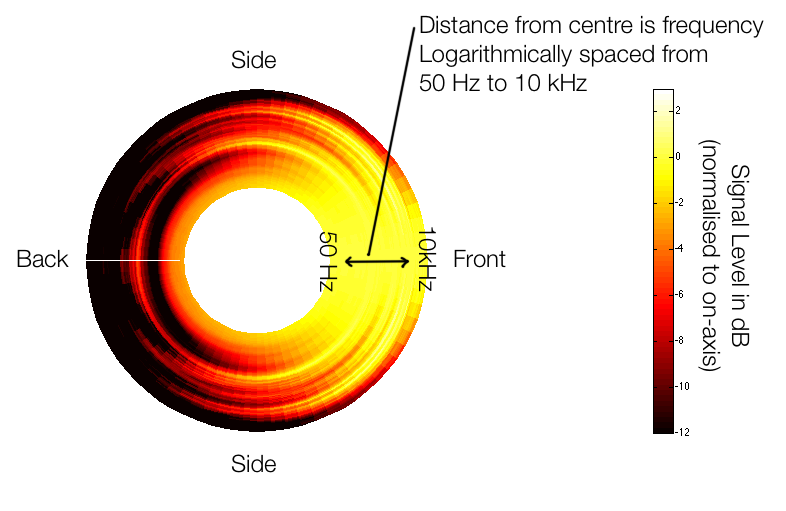
Figure 1, above, shows the idea. We have a loudspeaker, pointing to the right of the screen (towards the word “front”). We measure the magnitude response (more commonly called the “frequency response”) of the loudspeaker on-axis, directly in front of it. Then we rotate the angle of the listening position around the loudspeaker, towards the side. As we do, we measure how much the level changes (usually it gets quieter, but sometimes, at some frequencies and some angles, it gets louder) as a function of angle and frequency. As the angle to the listening position increases, some frequencies will get quiet very quickly, some will not get quiet at all – even when we reach the back of the loudspeaker.
The plot above shows one way to look at this. The inner rings are the low frequencies (in the case of the plots on this webpage, the inner-most ring is 50 Hz) and the further outwards you go, the higher in frequency. The distance between the rings is logarithmic (in other words, by octave) so it makes more sense musically.
If you’re used to looking at the contour plots that I typically show on this site, then take a look at Figure 2 which shows exactly the same data. In this case, it’s plotted as a contour plot (like a topographic map) showing the -3 dB, -6 dB, -9 dB, and -12 dB contours relative to the on-axis response.
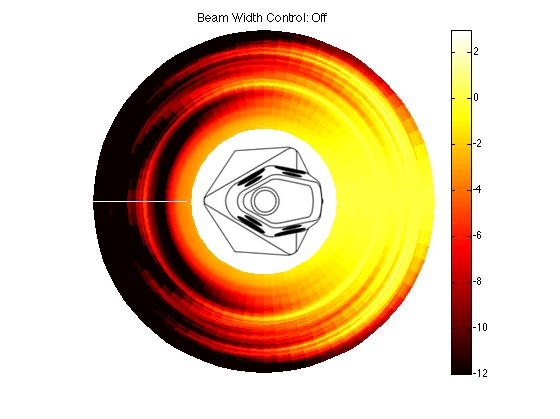
BeoLab 90: Beam Width Control: Off
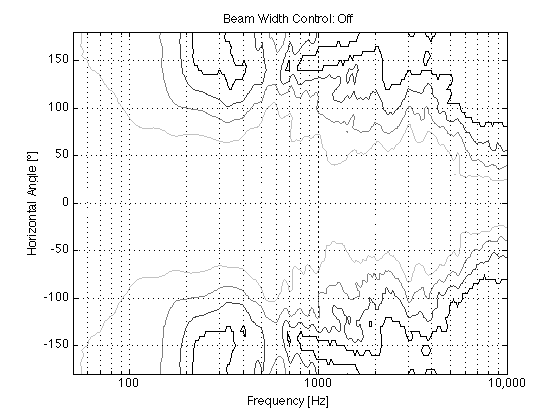
Figures 2 and 3 show the directivity of the BeoLab 90 if you were to disable the Beam Width Control function entirely and just use the front woofer, midrange and tweeter by themselves (and therefore turn off the 15 other loudspeaker drivers in the system. It’s important to note that this is not possible in a production model loudspeaker – we did it as part of the initial measurements of the loudspeaker during the development process.
BeoLab 90: Narrow Beam
As I’ve discussed in other postings, our goal with BeoLab 90’s directivity was two-fold: The first was to have a constant directivity – meaning that it should be the same at all frequencies. The second was that the directivity should be narrow in order to reduce the influence of sidewall reflections. Of course, it should not be too narrow – you don’t want a loudspeaker that you can hear in your left ear, but not your right or “headphones at a distance” as I read on one website.
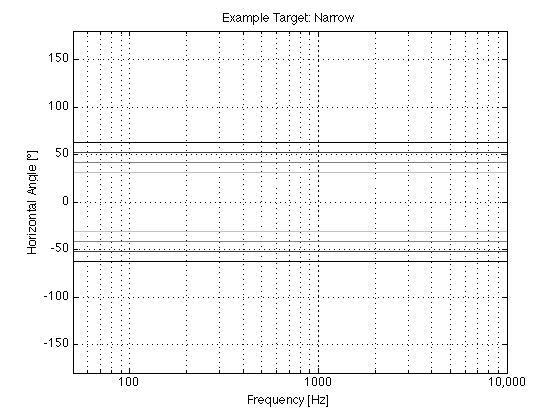
So, we played around with different target directivity functions during the development process, trying to find a beam width that was not too wide and not too narrow. Figures 4 and 5 aren’t drawings of the actual target for BeoLab 90 – but they’re illustrative of the concept.

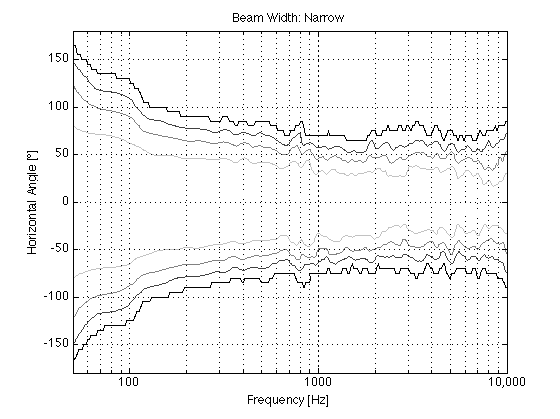
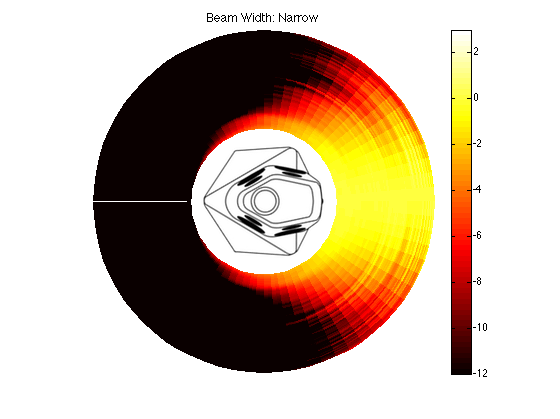
The actual directivity of the narrow beam width in BeoLab 90 is plotted in Figures 6 and 7.
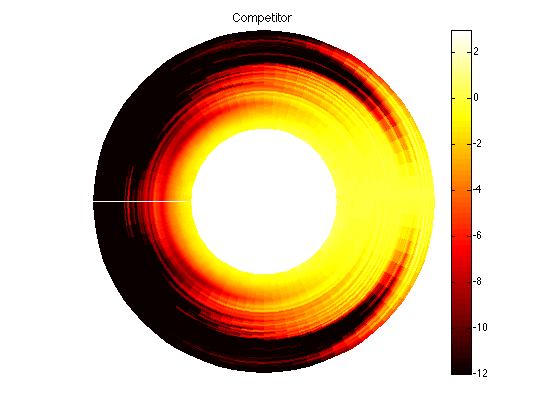
It might also be interesting to compare this to one of BeoLab 90’s competitors from another manufacturer, shown in Figure 8.
BeoLab 90: Wide Beam
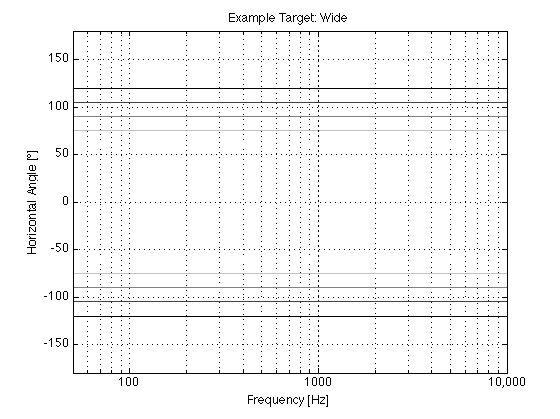
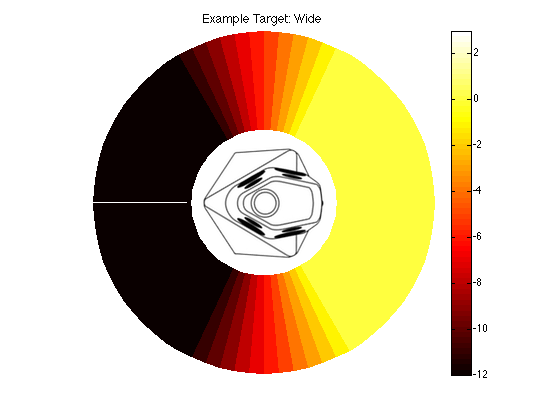
Again, we can look at a candidate for a target (but not the target) for the wide beam mode. This is shown in Figures 8 and 9.
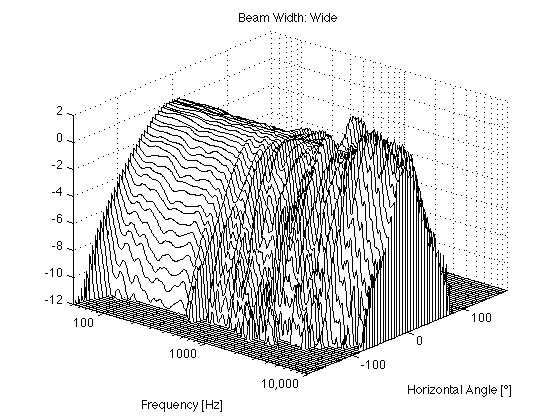
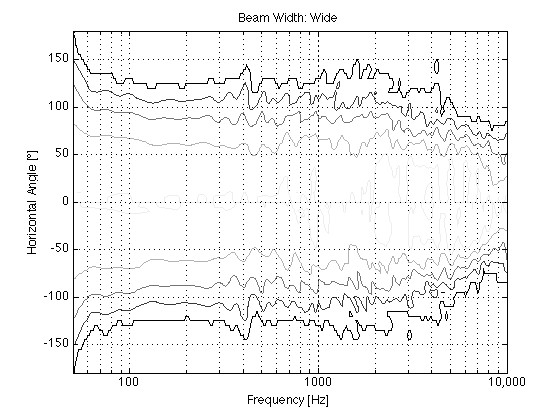
The actual directivity of the wide beam is shown in Figures 10 and 11.
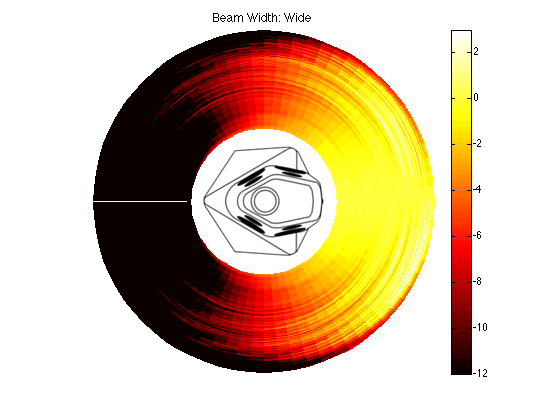
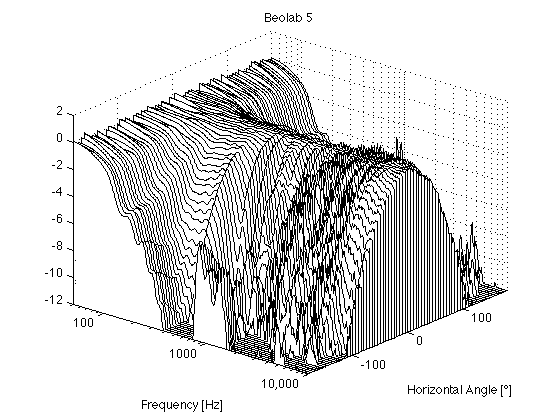
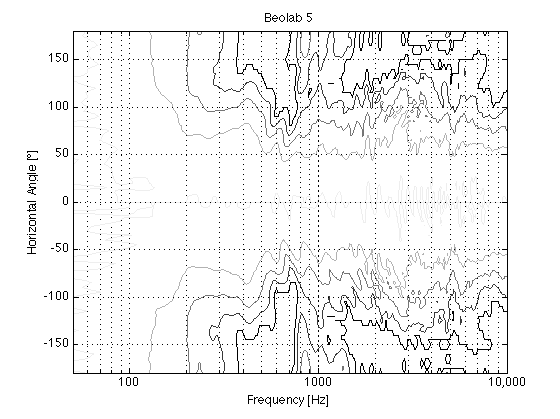
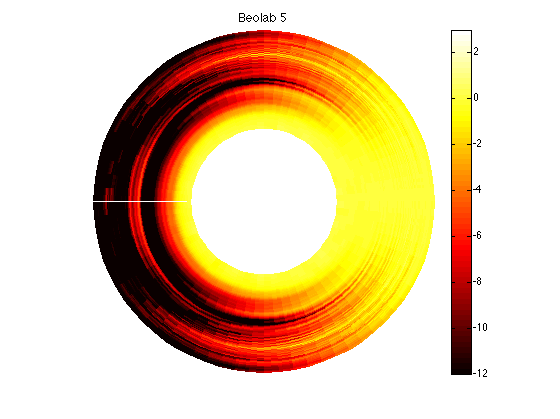
In addition, it might be interesting to compare those plots to the BeoLab 5 directivity, which had similar targets of a constant and wide directivity.
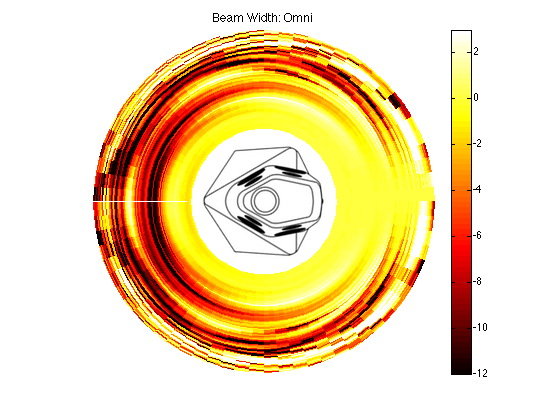
BeoLab 90: Omni Beam
The directivity of BeoLab 90’s Omni mode is shown below in Figures 15 and 16. The lobing caused by the distances between the tweeters is visible in the contour plot, however, as you can see in Figure 16, there is certainly energy being directed in all directions across the entire frequency spectrum. However, the high-frequency lobing, in addition to the beaming in the lower midrange area would indicate that this mode is not appropriate for critical listening…

Some details
The plots above were done in the horizontal plane with a smoothing of 1/12 octave (by semitone).
The measurements on the loudspeakers were done in 73 increments of 5º from -180º to 180º (in other words, we’re actually measuring both sides of the loudspeaker – we don’t just measure one side and assume the directivity is symmetrical.






