Inspired by a conversation with Jamie Angus following my last posting, I did some digging into the probability density functions (PDF’s) of a bunch of test tracks that I use for tuning and testing loudspeakers.

The plots below are the results of this analysis.

Some explanations, to start…

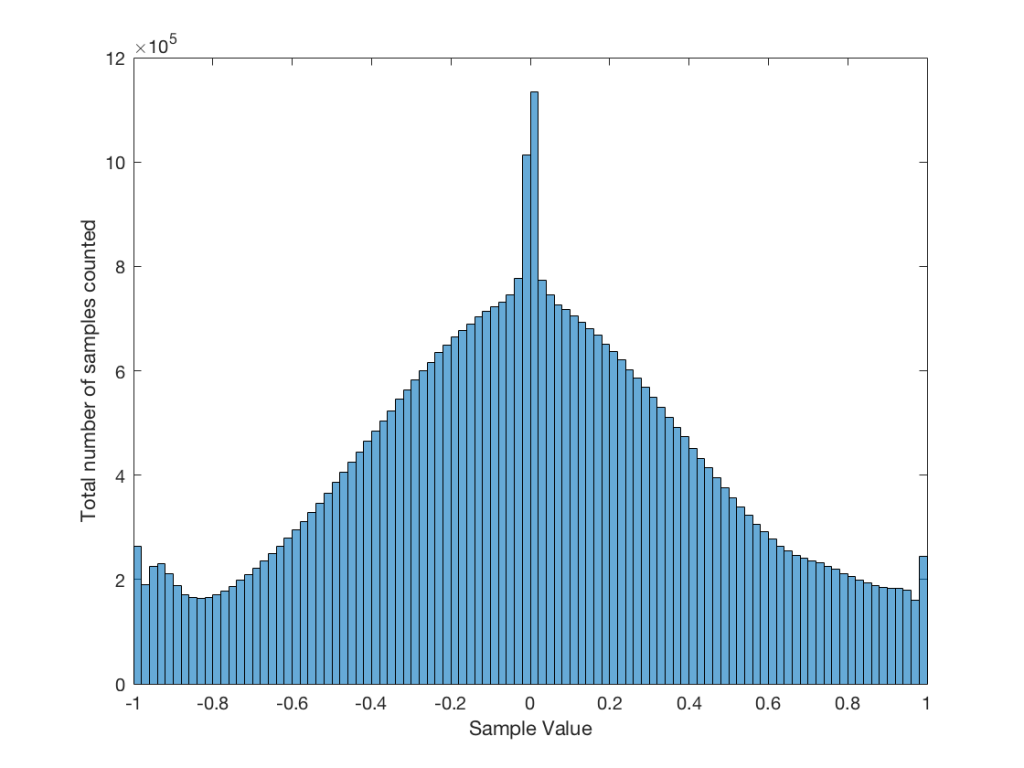
A PDF of an audio signal is a measurement of the probability that a given level (or sample value) will happen in a given period of time. In the case of the plots below, I just counted each time every sample value the 16-bit range of possibilities (from -32768 to 32767, if you think in binary – from -1 to +1-2^-15 in steps of 2^-15 if you prefer to think in floating point decimal) occurred in an entire track (usually the full tune). That’s plotted below as the gray “curve” in a linear world.

I converted the linear levels to “instantaneous” (sample-by-sample) dB values (since they’re instantaneous, they’re not in dB FS – but let’s not get into that discussion), but kept the positive and negative polarities of the linear values separate. Those are plotted as the red (negative values, expressed in dB) and black (positive values, expressed in dB). I cheated a little here, since a linear value of “0” isn’t really -96 dB – it’s -infinity dB… but, except for that one value, everything else is plotted correctly.

When I did these analyses, I noticed lots of sample values in lots of tracks that had no probability of ever occurring. Sometimes, this is just because the track is mastered low in level – so the “upper” sample values are not used. Sometimes, there are “dead values” well inside the range. This likely points to an error in the converter and/or digital mixing and/or mastering equipment.

Finally, I made a plot of the number of “dead” sample values per 128 sample values in 512 blocks (65536/128 = 512). That’s the red line above the gray one.

Some other things are noticeable in the plots, but we’ll take those as they come, below…

Note that I will not reveal the names of the tracks I used, since it’s not my purpose here to make anyone look bad. It’s to look at the differences between different recordings, types, and even equipment… Don’t ask which recordings I used.

This plot of an orchestral recording (“orchestral8”) looks fairly normal. As Jamie pointed out in the last posting, the distribution looks to be Laplacian. There is a big spike at the “0” mark – due to the silence at the beginning and end of the track. As can be seen, the track peaks around a linear value of about +/- 0.2 or about -14 dB below full scale. So, the sample values above 0.2 (or below -0.2) are unused. This can be seen in the blue lines (comprised of a blue dot at each sample value) in the top plot, and the red line at 128 (the number of “dead values” per 128 possible values) in the bottom plot.

The “solo inst3” is very similar in behaviour, even though it’s a completely different recording. This one is of a solo stringed instrument in a fairly reverberant space. Notice that its basic characteristics are very similar to those shown in “orchestra8”.

The “voice3” recording is also similar. It’s a little interesting in all three of these recordings to note the transition between levels where there are no dead sample values (around the “0” line) and levels where there are nothing but dead values. In this area (in the “voice3” recording, for example, around +/- 0.3, there are sample values that are used – but others that are skipped. This is because the track has a reasonably large crest factor (the ratio between the peak and the RMS of the track) – in other words, it has noticeable peaks. When the levels peak positively or negatively, there will be some values skipped along the way…

Although these are very different recordings of different instruments in different spaces on different labels – they all appear to have some characteristics in common.

They very likely had little or no compression applied
They don’t use the entire dynamic range available. This is not necessarily a bad thing, since it could be that each of those tracks was part of a larger collection, and its level made sense in the context of the entire album.

Now let’s look at another acoustic recording that was done with four microphones, and no compression – but possibly some small processing done in the mastering.

Obviously the “orchestra6” recording has something strange going on. It almost looks as though something in the recording chain “favoured” every second sample value – hence the zig-zag pattern in the probability density function. Note that this was not a small thing – the difference in how much the sample values are “preferred” is by a factor of 10.

What could cause this? This is difficult to say by just looking at this plot, since we have to remember that these values are complied using the entire track. So, for example, three possibilities that come immediately to mind are:

for some strange reason, the analogue-to-digital converter, or one of the DSP blocks in the mastering console “liked” every second sample value 10 times more than the others
for some other strange reason, the original ADC only used every second sample value – and one 10th of the track was edited together (or “spliced”) from a different take that needed extra gain.
something else

To be honest, I think that the first or third of these is more likely than the second – but either way, it certainly looks weird…

This track of another solo instrument (hence “solo inst1”) is a little different – but not terribly so. There is a little flatter behaviour in the upper plot, which corresponds to a more convex “umbrella” shape in the lower one – but generally, this is nothing serious to raise any eyebrows in my opinion… It probably indicates some minor compression.

Let’s look at some other tracks with compression…

“testtracks4” and “pop21” both have indications of compression in the flat response of the top plots and the convex shape of the lower ones. The “pop21” track has the added indication of clipping – the spikes on the sides of the plots. This indicates that we have an unusual number of samples with values of either -1 or +1. Note, however, that we do not move smoothly into that clipping – it was what we call “hard clipping”, since the values just before the +/- 1 values show no indication of a smooth transition to the spike.

The “bass20” track is interesting, not only because of the compression, but the apparent lack of silence (notice there is no spike around the “0” line). This is because this track is from a live album that is intended for gapless playback – and I just grabbed the track. So, it starts and stops with a hard transition to and from audience sound – there is no fade in or fade out.

The “bass2” track also has the spikes on the ends, showing the clipping – but, as you can see, the plots (particularly the linear plot on the bottom) starts to slope upwards just before the spike – indicating some kind of soft clipping or a peak limiting function was used to shape the envelope.

The “bass15” track is interesting, since it has the characteristic spikes on the sides that look a little like clipping (especially if you only look at the upper plot) but, as can be seen in the bottom plot, these are not at values of -1 or +1. So, this would indicate either that something else in the recording chain clipped – and then was smoothed out and reduced in level a little later in the process – or we’re looking at some kind of interesting soft-clipping processor that keeps a little “bump” in the envelope of the signal above the “clipping” area.

Now let’s look at some really strange ones…

I have no explanation for the plot in “testtracks6”. I can’t understand what would cause that bump only in the negative portion of the signal around -70 dB FS. My guess is that this is some sort of weird watermark that is inserted – but this is really stretching my imagination… Of course, if could just be that something in the processing chain is just broken… Anyone reading this have any good ideas? Seems to me that I should do a little more digging into this track to see what’s going on around those sample values…

The “pop11” track is an example of a recording that was probably done on early digital recording gear – or an early digital mastering console. As can be seen in both plots, there are missing sample values across the entire range of possible values.

One possible explanation of this is that this is a digital recording that had gain applied to it using a processor that did not use dither. This would cause the signal to not use every second sample value (or every third or fourth – depending on the gain applied). It’s also possible that it was processed or recorded using a device that had a “stuck bit”. I’ll do some simulations to show what that would look like and publish the plots in a future posting.

Note that the small “spikes” of peak limiting (looking a little like clipping on a small scale) are visible in the bottom plot – but they’re very small…

Some more recordings with strangely dead sample values are shown below. Note that some of these are very recent recordings – so the “early digital gear” excuse doesn’t hold up for all of them…

So, something is obviously broken in all four of these examples… Please don’t ask me how to explain them. The only thing I can do is to suspect that at least one piece of gear and/or software that was used in the late stages of the process was really broken… I just hope that, whatever gear/software it was, it didn’t cost a lot of money….

An interesting pair of examples are shown below…

The “jazz1” and “jazz2” recordings both come from the same album released by a small jazz ensemble. Notice that, although they are different tracks, they have similar PDF’s, seen in the “spikes” through the upper plots. It seems that there is something weird going on in the mastering console (or software) in this case – or perhaps the final mixing console…

The “speech4” track has obvious “favouring” of alternate sample values – but this was a track that was recorded on a very early DAT machine about 35 years ago… To be honest, knowing what I know about using an identical model DAT recorded, I’m surprised this looks as good as it does…

I’ll just put in a bunch more plots without comment – just to let you see some of the variety that shows up with this kind of analysis.

Post-script

This posting has a Part 2 that you’ll find here, and a Part 3 that you’ll find here.

Noise, Averages, and Incorrect Assumptions, Part 1

Let’s talk about the subject of noise. To begin with, we have to agree on a definition, which might become the biggest part of the problem. For normal people, going about their daily lives, “noise” is a word that usually means “unwanted sound”, as the Grinch explained, just before hitching up his dog to a sleigh:

However, “noise” means something else to an audio professional, who is consequently not “normal” and does not have a life – daily or otherwise.

When an audio professional says “noise”, they mean something very specific – “noise” is an audio signal that is random. For example, if the noise signal is digital, there would be no way to predict the value of the next sample – even if you know everything about all previous samples.

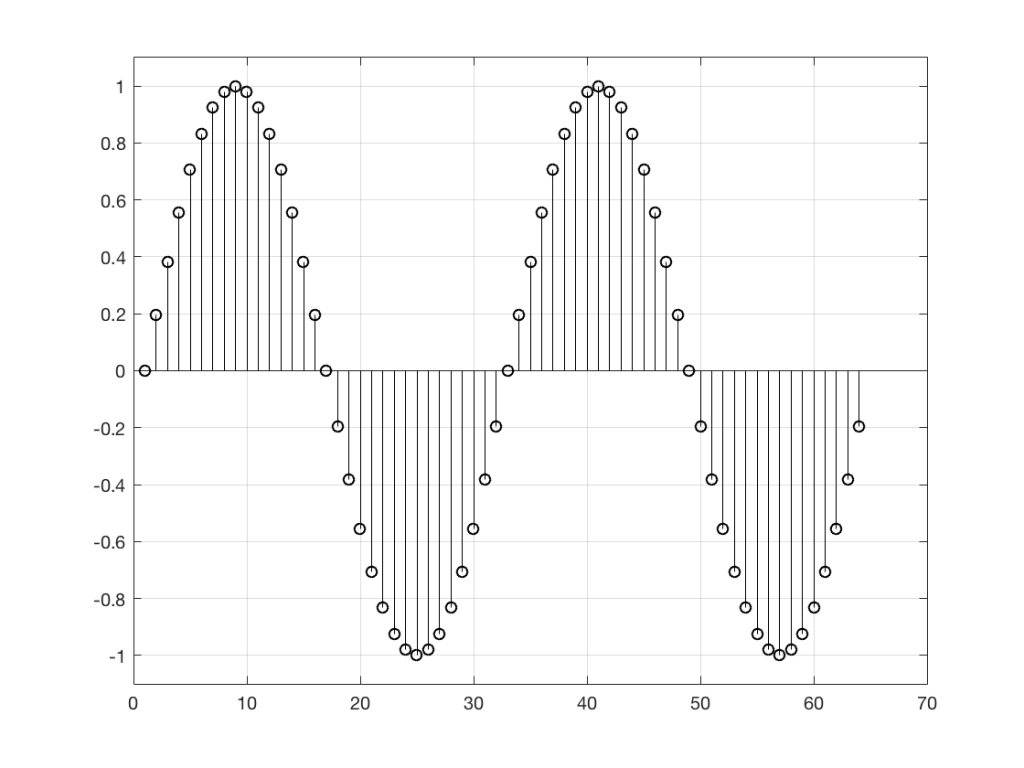
Figure 1: It would be fairly easy to guess the value of the next sample in the signal (#65), based on looking at what has happened before. This is because the signal is, as far as we can see here, periodic – meaning that it repeats itself – meaning that it repeats itself…

Figure 2: It’s impossible to predict the next value in the sequence, because there is no pattern in the previous samples. Each value is a random number between -1 and 1, and the next random number is, in no way, related to the ones before it.

So, “noise”, according to the professionals, is a signal made of a random sequence. However, we can be a little more specific than this. For example, in order to make the noise plotted in Figure 2, above, I asked Matlab to generate 64 random numbers between -1 and 1 using the code

rand(1,64)*2-1

So, although this will generate random numbers for me (we’ll assume for the purposes of this discussion that Matlab is able to generate truly random numbers… actually they’re “pseudorandom” – but let’s pretend for today…), there are some restrictions on those values. No matter how many random values I ask for using this code, I will never get a value greater than 1 or less than -1.

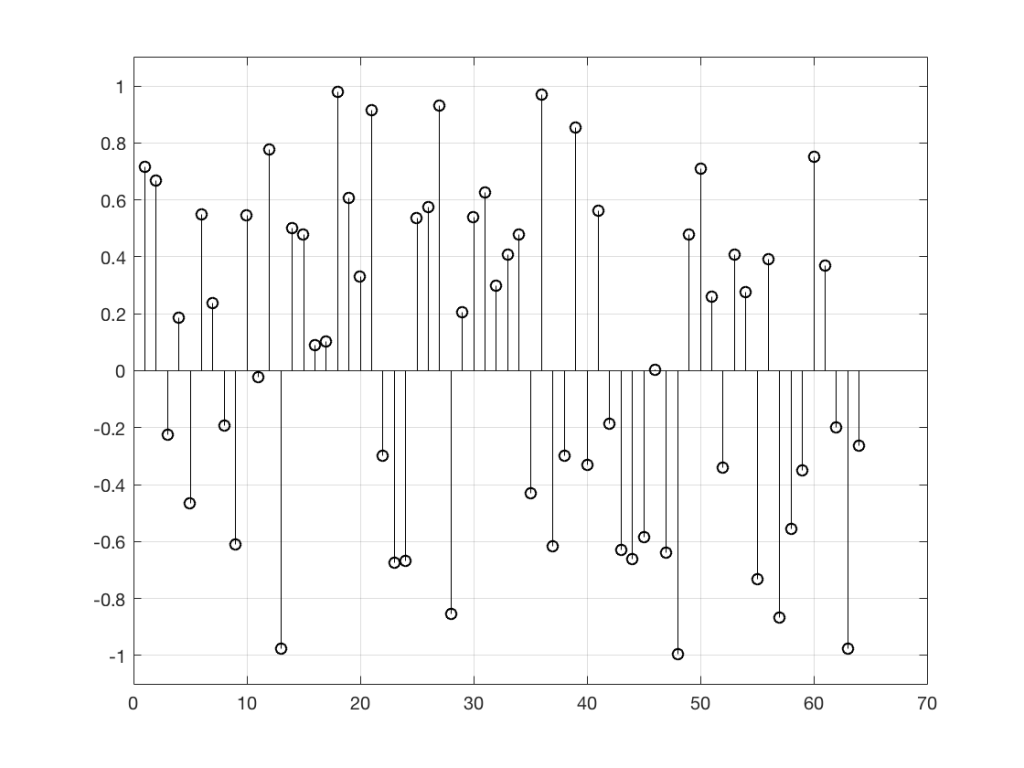
However, if I used a slightly different Matlab function – “randn” instead of “rand”, using the following code

randn(1,64)

I would get 64 random numbers, but they are not restricted as my previous bunch were, as you can seen in Figure 2a, below.

Again, it’s impossible to guess what the next value will be, but now you can see that it might be greater than 1 or less than -1 – but it will more likely to be closer to 0 than to be a “big” number.

So, Figures 2 and 2a show two different types of noise. Both are random numbers, but the distribution of the numbers in those two sequences are different.

To be more specific:

Let’s use the “rand(1,1000000)*2-1” function to make a sequence of 1,000,000 samples. We know that this will produce values ranging from -1 to 1. So, we’ll divide this range into 100 steps (-1.00 to -0.98, -0.98 to -0.96, -0.96 to -0.94, … and so on up to 0.98 to 1.00 – I know, I know, there’s some overlap here, but I didn’t want to use a bunch of less than or equal to symbols… The concept is the important point here… Back off!). For each of those divisions, we’ll count how many of the 1,000,000 samples fall inside that smaller range, and we’ll plot it. This is shown in Figure 3a.

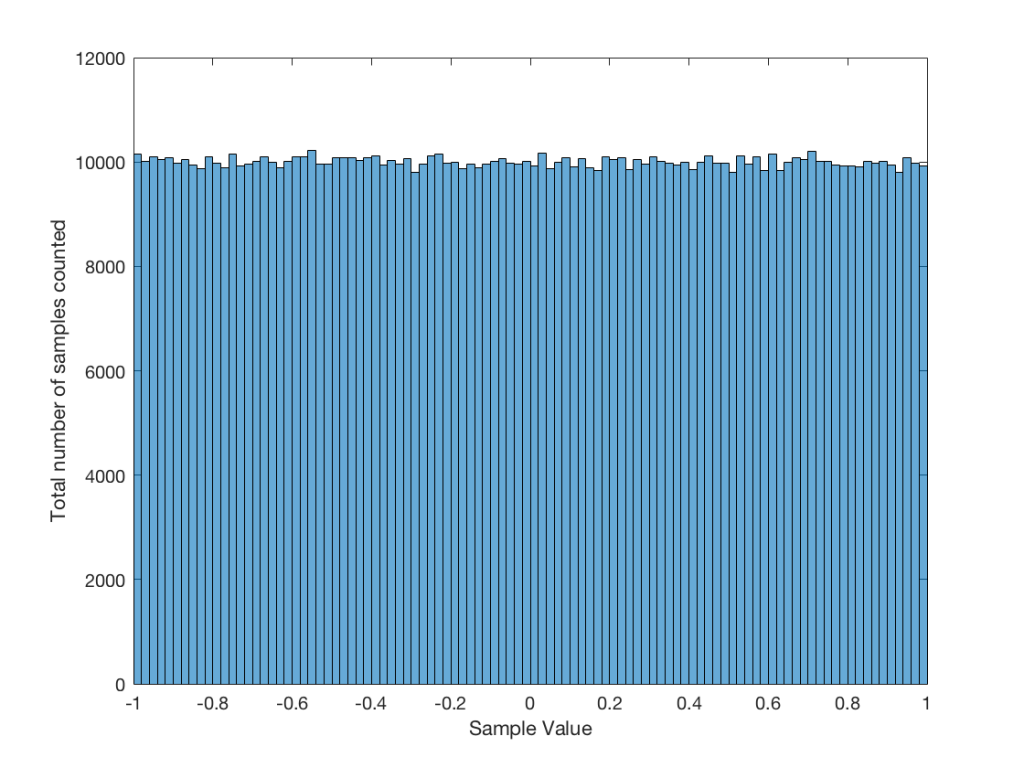
As you can see in Figure 3a, there are about 10,000 samples in each “bin”. This means that about 10,000 samples have a value that fall within each of the smaller slices of the total range. Also, if I added up the values of all 100 of those numbers plotted in 3a, I would get 1,000,000, since that’s the total number of values that we analysed.

If I do the same thing to the numbers coming out of the other function: “randn(1,1000000)” it would look very different. As we already saw, the numbers can be outside the range of -1 to 1, and they’re more likely to be around 0 than to be far away from it. This can be seen in Figure 3b.

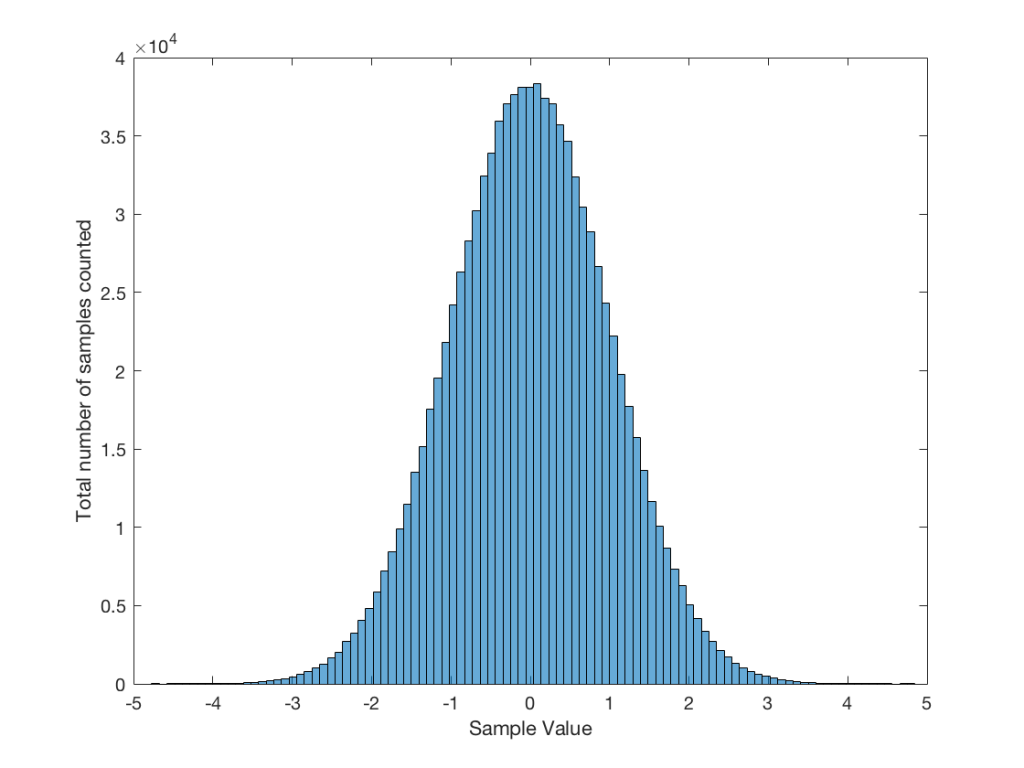
Figure 3b: A plot showing the distribution of the values of 1,000,000 samples generated by the Matlab code “randn(1,1000000)”.

Just to clean up a loose end – there are official terms to describe these differences. The noise plotted in Figure 2 has what is called a “rectangular distribution” because a plot of the distribution of the values in it (if we measure enough sample values) eventually looks like a rectangle (a blue rectangle, in the case of Figure 3a). The noise plotted in Figure 2a has a “normal distribution”, as can be seen in the bell-like shape of the plot in Figure 3b. There are many other types of distributions (for example, rolling 2 dice will give you random numbers with a “triangular distribution”), but we’ll leave it at 2 for now.

So, we’ve seen that we can have at least two different “types” of random number sets – but let’s do a little more digging.

Frequency content

Here’s where things get a little interesting. If I take the 1,000,000 samples that I used to make the plot in Figure 3a and I pretend it’s an audio signal, and then calculate the frequency content (or spectrum) of the signal, it would look like the green plot in Figure 4a, below. If I did a frequency analysis of the signal used to make the plot in Figure 3b, it would look like the red plot.

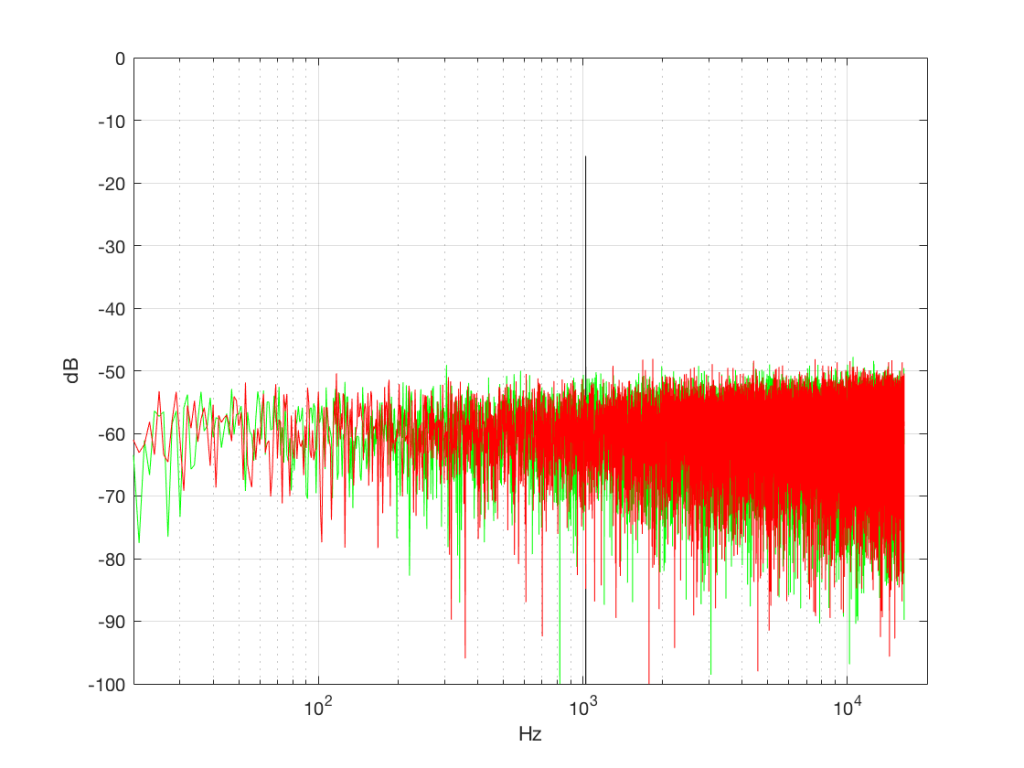
What’s interesting about this is that, basically speaking, the two signals, although they’re very different, have basically the same spectra – meaning they have the same frequency content, and therefore they’ll sound the same. This is really evident if I smooth these two plots using, for example, a 1/3 octave smoothing function, as is shown below in Figure 4b.

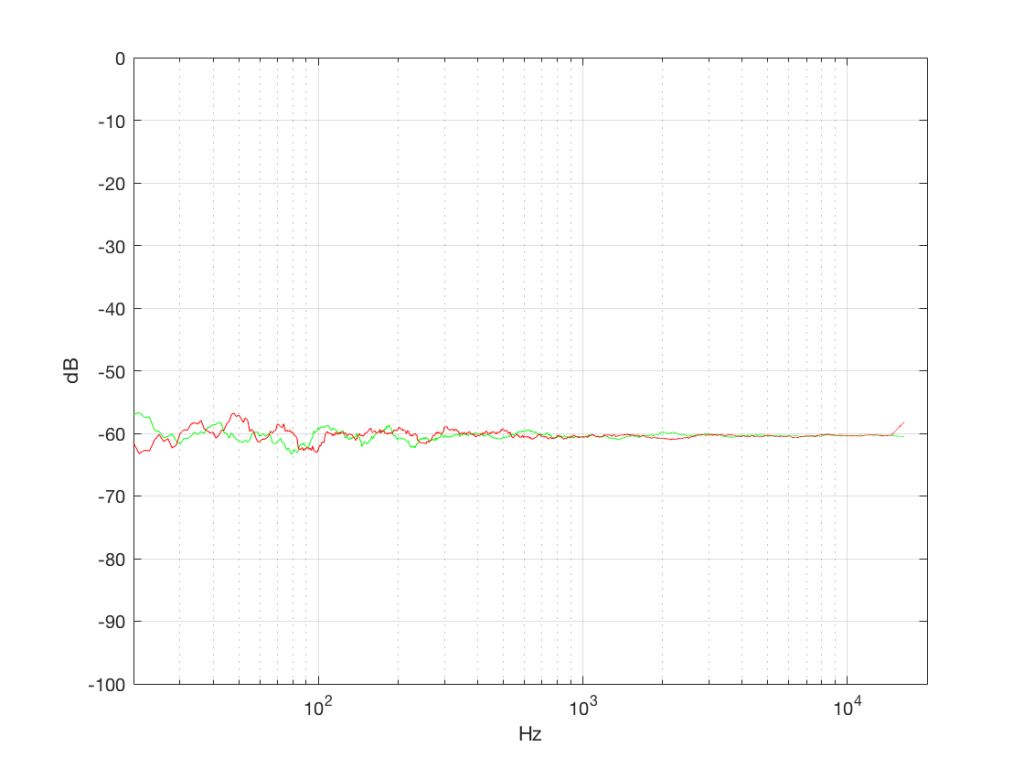
As you can see there, the very fine peaks and dips in the response shown in Figure 4a, when averaged, smooth to the flat response shown in Figure 4b.

Now we have to clear up a couple of issues…

The first is that, as you can see in the plot above, the spectrum of both random signals (both noise generators) is flat. However, due to the way that I did the math to calculate this, this means that we have an equal amount of energy in equal-sized frequency ranges throughout the entire frequency range of the signal. So, for example, we have as much energy from 20-30 Hz as we do from 1000-1010 Hz as we do from 10,000 – 10,010 Hz. In other words, we have equal energy per Hz. This might be a little counter-intuitive, since we’re looking at a semilogarithmic plot (notice the scale of the x-axis) but trust me, it’s true. This means that, in both cases, we have what is known as a “white noise” signal – which is a colourful way of saying “noise with an equal amount of energy per Hz”.

The second thing is that I just lied to you. In order to get the pretty plots in Figures 4a and 4b, I had to take long signals and analyse how much energy we got, over a long period of time. If I had taken a shorter slice of time (say, 100 samples long) then the spectra plots would not have looked as pretty – or as flat. For example, if I just take the first 100 samples of both of those noise generator outputs, and calculate the spectra in those, I get the plots in Figure 4c, below.

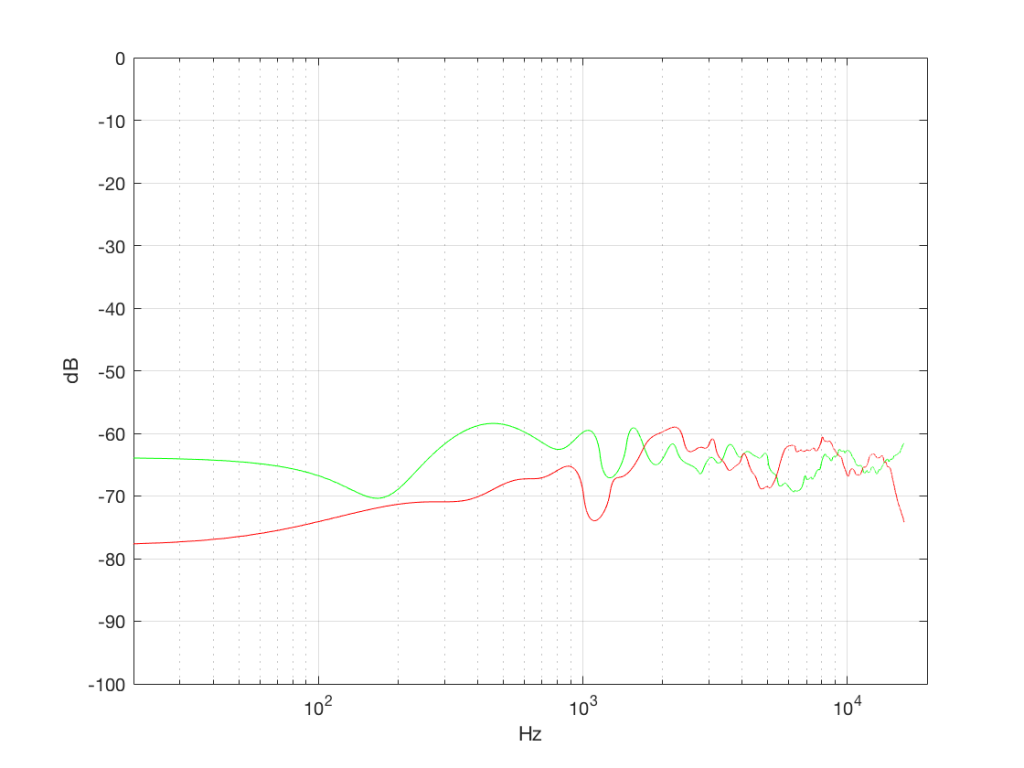
Figure 4c: The spectra in the first 100 samples of the signals analysed in Figures 4a and 4b.

Notice that these plots do not look nearly as flat – even though I’ve smoothed them with a 1/3 octave smoothing filter again. Why is this?

Well, the problem is probability. Since the two signals are random, there is no guarantee that all frequencies will be contained in them for any one little slice of time. However, there is an equal probability of getting energy at all frequencies over time. So, in a really strange universe, you might get all frequencies below 1000 Hz for one second, and then all frequencies above 1000 Hz for the next second – over two seconds, you get all frequencies, but at any one moment, you don’t.

What this means is that “white noise” doesn’t necessarily contain energy at all frequencies equally – unless you wait for a long time. If you listen for long enough, all frequencies will be represented, but the shorter the measurement, the less “flat” your response.

Just for the purposes of comparison, let’s also find out what the distribution of values is for a sine wave – since this might be interesting later… This is shown in Figure 5, below.

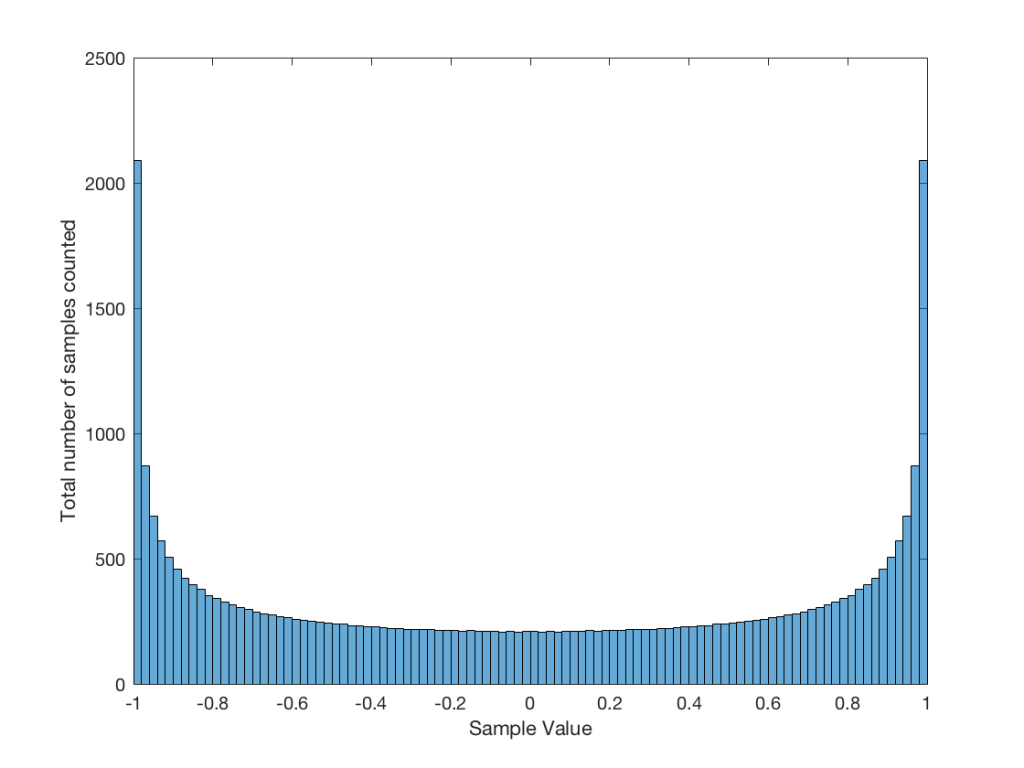
Fig 5: The distribution of values in a sine wave that has a peak value of 1. Basically, what this plot means is that, on average, a sine wave doesn’t spend much time around “0” – and it spends a lot of time out at the extremes.

It may be interesting to note that “normal” sounds like music and speech have distributions that look much more like Figure 3b than like Figure 5, as is shown in the examples in Figures 6, 7, and 8. This is why you shouldn’t necessarily use a sine wave to measure a piece of audio equipment and draw a conclusion about how music will sound…

Fig 6. The distribution of values for an anechoic recording of female voice, made without any processing. A non-anechoic recording of any voice would have a similar shape…

Fig 7. The distribution of values in a recording of a Brandenburg Concerto that I happen to like.

Fig 8. The distribution of values in the samples in the first 60 seconds of “Smells Like Teen Spirit” by Nirvana.

Fig 9: The distribution of all of the samples in Metallica’s “The Day that Never Comes”. This one is admittedly pretty strange – but that won’t come as a surprise to many people.

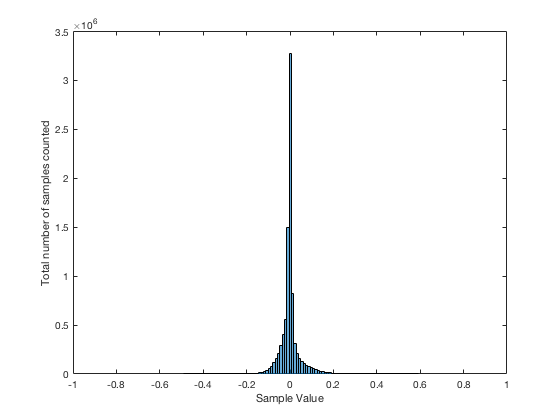
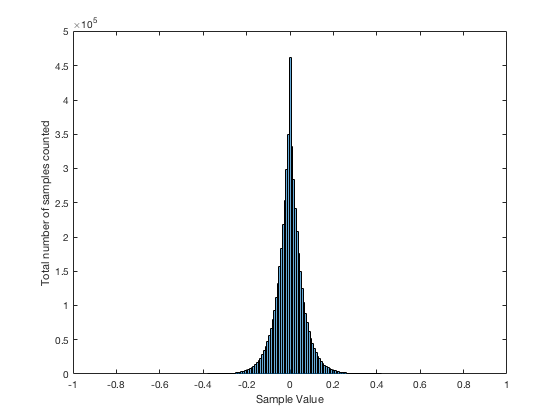
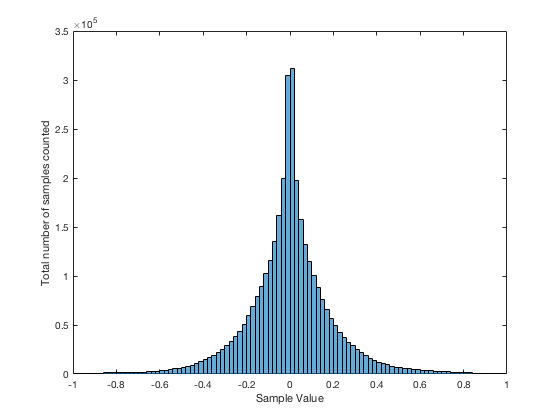
Averaging

If I play the first kind of white noise (the one shown in Figure 2) and measure how loud it is with a sound pressure level meter, I’ll get a number – probably higher than 0 dB SPL (or else I can’t hear it) and hopefully lower than 120 dB SPL (or else I’ll probably be in pain…). Let’s say that we turn up the volume until the meter says 70 dB SPL – which is loud enough to be useful, but not loud enough to be uncomfortable.

Then, I switch to playing the other kind of white noise (the one shown in Figure 2a) and turn up the volume until it also measures 70 dB SPL on the same meter.

Then, I switch to playing a sine wave at 1 kHz and turn up the volume until it also reads 70 dB SPL.

If I were to compare what is coming into the loudspeaker for each of those three signals, after they have been calibrated to have the same output level, they would look like the three signals in Figure 9.

Fig 9: Three different signals, all calibrated to have the same output level when measured with a meter that doesn’t know anything about frequency content. The green signal is white noise as shown in Figure 2. The red plot is white noise as shown in Figure 2a. The black plot is a sine wave.

These will all sound roughly the same level, but as you can see in the plot in Figure 9, they do not have the same PEAK level – they have the same average level – averaged over time…

However, if we were to do a frequency-dependent analysis of these three signals, one of these things would not look like the others… Check out Figure 4a, which I’ve copied below…

Notice that, in a frequency-dependent analysis, the sine wave (the black line sticking up around 1000 Hz) looks much louder (35 dB louder is a lot!) than the green plot and the red plot (our two types of white noise). So, even though all three of these signals sound and measure to have roughly the same level, the distribution of energy in frequency is very different.

Another way to think about this is to say that each of the three signals has the same energy – but the sine wave has all of it at only one frequency all the time – so there’re more energy right there. The noise signals have the energy at that frequency only some of the time (as was explained above…).

ANOTHER way to think about this is to put a glass of water in the bottom of an empty bathtub. If the depth of the water in the glass is 10 cm – and you pour it out into the tub, the depth of the water will be less, since it’s distributed over a larger area.

As you can see in the title of this posting, this is “Part 1″… All of this was to set up for Part 2, which will (hopefully) come next week. As a preview: the topic will be the use (and mis-use) of weighting functions (like “A-weighting”) when doing measurements…

The second Neo to be interested in Simulacra and Simulation

A brief (and recent) history of reverberation

BeoLab 90 Review in Scandinavia

“Lyden av BeoLab 90 er vanskelig å forklare, den må egentlig bare oppleves. Personlig har jeg aldri hørt en mer livaktig musikkgjengivelse, og flere som har vært på besøk reagerte med å klype seg i armen eller felle en tåre når de hørte et opptak de kjente, eller rettere sagt trodde de kjente!”

“The sound of the BeoLab 90 is hard to explain, it must really be experienced. Personally I have never heard a more lifelike music reproduction, and several who have been visiting reacted by pinching their own arm or shedding a tear when they heard a recording they knew, or rather thought they knew!”