Author: geoff
B&O Tech: BeoLab loudspeakers and Third-party systems
#77 in a series of articles about the technology behind Bang & Olufsen loudspeakers
I’m occasionally asked about the technical details of connecting Bang & Olufsen loudspeakers to third-party (non-B&O) sources. In the “old days”, this was slightly difficult due to connectors, adapters, and outputs. However, that was a long time ago – although beliefs often persist longer than facts…
All Bang & Olufsen “BeoLab” loudspeakers are “active”. At the simplest level, this means that the amplifiers are built-in. In addition, almost all of the BeoLab loudspeakers in the current portfolio use digital signal processing. This means that the filtering and crossovers are implemented using a built-in computer instead of using resistors, capacitors, and inductors. This will be a little important later in this posting.
In order to talk about the compatibility issues surrounding the loudspeakers in the BeoLab portfolio – both with themselves and with other loudspeakers, we really need to break the discussion into two areas. The first is that of connectors and signals. The second, more problematic issue is that of “latency” (which is explained below…)
Connectors and signals
Since BeoLab loudspeakers have the amplifiers built-in, you need to connect them to an analogue “line level” signal instead of the output of an amplifier.
This means that, if you have a stereo preamplifier, then you just connect the “volume-regulated” Line Output of the preamp to the RCA line inputs of the BeoLab loudspeakers. (Note that the BeoLab 3 does not have a built-in RCA connector, so you need an adapter for this). Since the BeoLab loudspeakers (except for BeoLab 5, 50, and 90) are fixed at “full volume”, then you need to ensure that your Line Output of the source is, indeed, volume-regulated. If not, things will be surprisingly loud…
In addition to the RCA Line inputs, most BeoLab loudspeakers also have at least one digital audio input. The BeoLab 5 has an S/P-DIF “coaxial” input. The BeoLab 17, 18, and 20 have optical digital inputs. The BeoLab 50 and 90 have many options to choose from. Again, apart from the BeoLab 5, 50, and 90, the loudspeakers are fixed at “full volume”, so if you are going to use the digital input for the BeoLab 17, 18, or 20, you will need to enable the volume regulation of the digital output of your source, if that’s possible.
Latency
Any audio device has some inherent “latency” or “delay from the time the signal comes in until it goes out”. For some devices, this latency can be so low that we can think of it as being 0 seconds. In other words, for some devices (say, a wire, for example) the signal comes out at the same time as it comes in (as far as we’re concerned… I’m not going to get into an argument about the speed of electricity or light, since these go very fast…)
Any audio device that uses digital signal processing has some measurable (and possibly audible) latency. This is primarily due to 5 things, seen in the flowchart below.
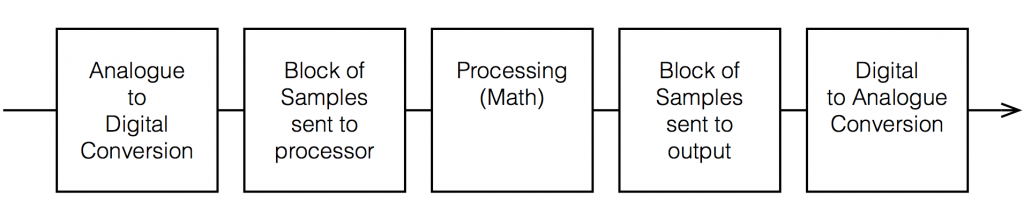
Each of these 5 steps each have different amounts of latency – some of them very, very small. Some are bigger. One thing to know about digital signal processing is that, typically, in order to make the math more efficient (and therefore squeeze as much as possible out of the computing power), the samples are processed in “blocks” – not one-by-one. So, the signal comes into the input, it gets converted to individual samples, and those samples are collected into a block of 64 samples (for example) before being sent to the processing.
So, let’s say that you have a sampling rate of 44100 samples per second, and a block size of 64 samples. This then means that you send a block to the processor every 64 * 1/44100 = 1.45 ms. That block gets processed (which takes some time), and then sent as another block of 64 samples to the DAC (digital to analogue converter).
So, ignoring the latency of the conversion from- and to-analogue, in the example above, it will take 1.45 ms to get the signal into the processor, you have a 1.45 time window to do the processing, and it will take another 1.45 ms to get the signal out to the DAC. This is a total of 4.35 ms from the instant a signal gets comes into the analogue input to the moment it comes out the analogue output.
Sidebar: Of course, 4.3 ms is not a long time. If you had a loudspeaker outdoors, then adding 4.35 ms to its latency would be same delay you would incur by moving 1.5 m (or about 4.9 feet) further away. However, in terms of a stereo or multichannel audio system, 4.35 ms is an eternity. For example, if you have a correctly-configured stereo loudspeakers (with each loudspeaker 30º from centre-front, and you’re sitting in the “sweet spot”, if you delay the left loudspeaker by just 0.2 ms, then lead vocals in your pop tunes will move 10º to the right instead of being in the centre. It only takes 1.12 ms of delay in one loudspeaker to move things all the way to the opposite side. In a multichannel loudspeaker configuration (or in headphones), some of the loudspeaker pairs (e.g. Left Surround – Right Surround) result in you being even more sensitive to these so-called “inter-channel delay differences”.
Also, the amount of time required by the processing depends on what kind of processing you’re doing. In the case of BeoLab 50 and 90, for example, we are using FIR filters as part of the directivity (Beam Width and Beam Direction) processing. Since this filtering extends quite low in frequency, the FIR filters are quite long – and therefore they require extra latency. To add a small amount of confusion to this discussion (as we’ll see below) this latency is switchable to be either 25 ms or 100 ms. If you want Beam Width control to extend as low in frequency as possible, you need to use the 100 ms “Long Latency” mode. However, if you need lip-synch with a non-B&O source, you should use the 25 ms “Low Latency” mode (with the consequent loss of directivity control at very low frequencies).
Latency in BeoLab loudspeakers
In order to use BeoLab loudspeakers with a non-B&O source (or an older B&O source) , you may need to know (and compensate for) the latency of the loudspeakers in your system. This is particularly true if you are “mixing and matching” loudspeakers: for example, using different loudspeaker models (or other brands – *gasp*) in a single multichannel configuration.
| Model | A / D | Latency (ms) | Equivalent in m | Volume Regulation? |
| Unknown analogue | A | 0 | 0 | No |
| Beolab 1 | A | 0 | 0 | No |
| Beolab 2 | A | 0 | 0 | No |
| Beolab 3 | A | 0 | 0 | No |
| Beolab 4 | A | 0 | 0 | No |
| Beolab 5 | D | 3.92 | 1.35 | Yes |
| Beolab 7 series | A | 0 | 0 | No |
| Beolab 9 | A | 0 | 0 | No |
| Beolab 12 series | D | 4.4 | 1.51 | No |
| Beolab 17 | D | 4.4 | 1.51 | No |
| Beolab 18 | D | 4.4 | 1.51 | No |
| Beolab 19 | D | 4.4 | 1.51 | No |
| Beolab 20 | D | 4.4 | 1.51 | No |
| Beolab 50 | D | 25 / 100 | 8.6 / 34.4 | Yes |
| Beolab 90 | D | 29 / 100 | 10.0 / 34.4 | Yes |
How to Do It
I’m going to make two assumptions for the rest of this posting:
- you have a stereo preamp or a surround processor / AVR that has a “Speaker Distance” or “Speaker Delay” adjustment parameter (measured from the loudspeaker location to the listening position)
- it does not have a “loudspeaker latency” adjustment parameter
The simple version (that probably won’t work):
Since the latency of the various loudspeakers can be “translated” into a distance, and since AVR’s typically have a “Speaker Distance” parameter, you simply have to add the equivalent distance of the loudspeaker’s latency to the actual distance to the loudspeaker when you enter it in the menus.
For example, let’s say that you have a 5.0 channel loudspeaker configuration with the following actual speaker distances, measured in the room.
| Channel | Model | Distance |
| Left Front | Beolab 5 | 3.7 |
| Right Front | Beolab 5 | 3.9 |
| Centre Front | Beolab 3 | 3.9 |
| Left Surround | Beolab 17 | 1.6 |
| Right Surround | Beolab 17 | 3.2 |
You then look up the equivalent distances in the first table and add the appropriate number to each loudspeaker.
| Channel | Model | Distance | + | Latency Equivalent | = | Total |
| Left Front | Beolab 5 | 3.7 | + | 1.35 | = | 5.05 |
| Right Front | Beolab 5 | 3.9 | + | 1.35 | = | 5.25 |
| Centre Front | Beolab 3 | 3.9 | + | 0 | = | 3.9 |
| Left Surround | Beolab 17 | 1.6 | + | 1.51 | = | 3.11 |
| Right Surround | Beolab 17 | 3.2 | + | 1.51 | = | 4.71 |
This technique will work fine unless the total distance that you have to enter in the AVR’s menus is greater than its maximum possible value (which is typically 10.0 m on most brands and models that I’ve seen – although there are exceptions).
So, what do you do if your AVR can’t handle a value that’s high enough? Then you need to fiddle with the numbers a bit…
The slightly-more complicated version (which might work most of the time)
When you enter the Speaker Distances in the menus of your AVR, you’re doing two things:
- calibrating the delay compensation for the differences in the distances from the listening position to the individual loudspeakers
- (maybe) calibrating the system to ensure that the sound arrives at the listening position at the same time as the video is displayed on the screen (therefore sending the sound out early, since it takes longer for the sound to travel to the sofa than it takes the light to get from your screen…)
That second one has a “maybe” in front of it for a couple of reasons:
- this is a very small effect, and might have been decided by the manufacturer to be not worth the effort
- the manufacturer of an AVR has no way of knowing the latency of the screen to which it’s attached. So, it’s possible that, by outputting the sound earlier (to compensate for the propagation delay of the sound) it’s actually making things worse (because the screen is delayed, but the AVR doesn’t know it…)
So, let’s forget about that lip-synch issue and stick with the “delay compensation for the differences in the distances” issue. Notice that I have now highlighted the word “differences” in italics twice… this is important.
The big reason for entering Speaker Distances is that you want the a sound that comes out of all loudspeakers simultaneously to reach the listening position simultaneously. This means that the closer loudspeakers have to wait for the further loudspeakers (by adding an appropriate delay to their signal path). However, if we ignore the synchronisation to another signal (specifically, the lips on the screen), then we don’t need to know the actual (or “absolute”) distance to the loudspeakers – we only need to know their differences (or “relative distances”). This means that you can consider the closest loudspeaker to have a distance of 0 m from the listening position, and you can subtract that distance from the other distances.
For example, using the table above, we could subtract the distance to the closest loudspeaker (the Left Surround loudspeaker, with a distance of 1.6 m) from all of the loudspeakers in the table, resulting in the table below.
| Channel | Model | Distance | – | Closest | = | Result |
| Left Front | Beolab 5 | 3.7 | – | 1.6 | = | 2.1 |
| Right Front | Beolab 5 | 3.9 | – | 1.6 | = | 2.3 |
| Centre Front | Beolab 3 | 3.9 | – | 1.6 | = | 2.3 |
| Left Surround | Beolab 17 | 1.6 | – | 1.6 | = | 0 |
| Right Surround | Beolab 17 | 3.2 | – | 1.6 | = | 1.6 |
Again, you look up the equivalent distances in the first table and add the appropriate number to each loudspeaker.
| Channel | Model | Distance | + | Latency equivalent | = | Total |
| Left Front | Beolab 5 | 2.1 | + | 1.35 | = | 3.45 |
| Right Front | Beolab 5 | 2.3 | + | 1.35 | = | 3.65 |
| Centre Front | Beolab 3 | 2.3 | + | 0 | = | 2.3 |
| Left Surround | Beolab 17 | 0 | + | 1.51 | = | 1.51 |
| Right Surround | Beolab 17 | 1.6 | + | 1.51 | = | 3.11 |
As you can see in Table 5, the end results are smaller than those in Table 3 – which will help if your AVR can’t get to a high enough value for the Speaker Distance.
The only-slightly-even-more complicated version (which has a better chance of working most of the time)
Of course, the version I just described above only subtracted the smallest distance from the other distances, however, we could do this slightly differently and subtract the smallest total (actual + equivalent distance) from the totals to “force” one of the values to 0 m. This can be done as follows:
Starting with a copy of Table 3, we get a preliminary Total, and then subtract the smallest of these from all value to get our Final Speaker Distance.
| Channel | Model | Distance (m) | + | Latency (m) | = | Total | – | Smallest | = | Final |
| Lf | BL 5 | 3.7 | + | 1.35 | = | 5.05 | – | 3.11 | = | 1.94 |
| Rf | BL 5 | 3.9 | + | 1.35 | = | 5.25 | – | 3.11 | = | 2.14 |
| Cf | BL 3 | 3.9 | + | 0 | = | 3.9 | – | 3.11 | = | 0.79 |
| Ls | BL17 | 1.6 | + | 1.51 | = | 3.11 | – | 3.11 | = | 0 |
| Rs | BL 17 | 3.2 | + | 1.51 | = | 4.71 | – | 3.11 | = | 1.6 |
Of course, if you do it the first way (as shown in Table 3) and the values are within the limits of your AVR, then you don’t need to get complicated and start subtracting. And, in many cases, if you don’t own BeoLab 50 or 90, and you don’t live in a mansion, then this will probably be okay. However… if you DO own BeoLab 50 or 90, and/or you do live in a mansion, then you should probably get used to subtracting…
Some additional information about BeoLab 50 & 90
As I mentioned above, the BeoLab 50 and BeoLab 90 have two latency options. The “High Latency” option (100 ms) allows us to implement FIR filters that control the directivity (the Beam Width and Beam Directivity) to as low a frequency as possible. However, in this mode, the latency is so high that you will notice that the sound is behind the picture if you have a non-B&O television.* In other words, you will not have “lip-synch”.
For customers with a non-B&O television*, we have included a “Low Latency” option (25 ms) which is within the tolerable limits of lip-synch. In this mode, we are still controlling the directivity of the loudspeaker with an FIR, but it cannot go as low in frequency as the “High Latency” option.
As I mentioned above, a 100 ms latency in a loudspeaker is equivalent to placing it 34.4 m further away (ignoring the obvious implications on the speaker level). If you have a third-part source such as an AVR, it is highly unlikely that you can set a Speaker Distance in the menus to be the actual distance + 34.4 m…
So, in the case of BeoLab 50 or 90, you should manually set the Latency Mode to “Low Latency” (using the setup options in the speaker’s app). This then means that you should add “only” 8.6 m to the actual distance to the loudspeaker.
Of course, if you are using the BeoLab 50 or 90 alone (meaning that there is no video signal, and no other loudspeakers that need time-alignment) then this is irrelevant, and you can just set the Speaker Distance to 0 m. You can also change the loudspeakers to another preset (that you or your installer set up) that uses the High Latency mode for best performance.
Instructions on how to do this are found in the Technical Sound Guide for the BeoLab 50 or the BeoLab 90 via the Bang & Olufsen website at www.bang-olufsen.com.
* Here a “B&O Television” means a BeoPlay V1, BeoVision 11, 14, Avant, Avant NG, Horizon, or Eclipse. Older B&O televisions are different… This will be discussed in the next blog posting.
Convenience vs. Quality
One way to compare CODEC quality
I’m often asked about my opinion regarding sound quality vs. compression formats or sampling rates or bit depths or psychoacoustic CODEC’s or other things like that…
Of course, there are lots of ways to decide on such an opinion, depending on what parameters you use to define “sound quality” and therefore what it is you’re asking specifically…
One way to think of this is to consider that the original sound file is the “reference” (regardless of how “good” or “bad” it is…), and when you encode it somehow (say, by changing sampling rates, or making it an MP3 file, for example), AND that encoding makes it different, then the resulting difference from the original can be considered an error.
So, I took a compilation of tracks that I often use for listening to loudspeakers. This is about 13 minutes long and is made of excerpts of many different recordings and recording styles, ranging from anechoic female speech, through a cappella choral, orchestral music, jazz, hard rock, heavy metal, and hip hop. The original tracks were all taken from 44.1 kHz / 16-bit CD’s, and the compilation is a 44.1 kHz / 16 bit result. This is what we’ll call the “reference”.
I then used LAME to encode the compilation in different bitrates of MP3. I re-encoded as 320, 256, and 128 CBR (Constant Bit Rate). I also used the “–preset” option to make encodings in the “insane”, “extreme”, “standard”, and “medium” settings (I’ve included the details of this at the bottom in the “Appendix”). Three of these four presets are VBR – the “Insane” setting is a CBR 320 kbps with some tweaked parameters.
I decoded those MP3 files back to PCM, and compared them to the original, of course making sure that everything was time- and gain-aligned. (There are some small differences in the overall level of the original file and the MP3 output – which is different for different bitrates. If I did not do this, then I would be exaggerating the differences between the original and the encoded versions – so this gain difference was calculated and compensated for, before subtracting the original from the MP3.)
Let’s take a look at a plot of the sample values in the left channel of the beginning of the track.
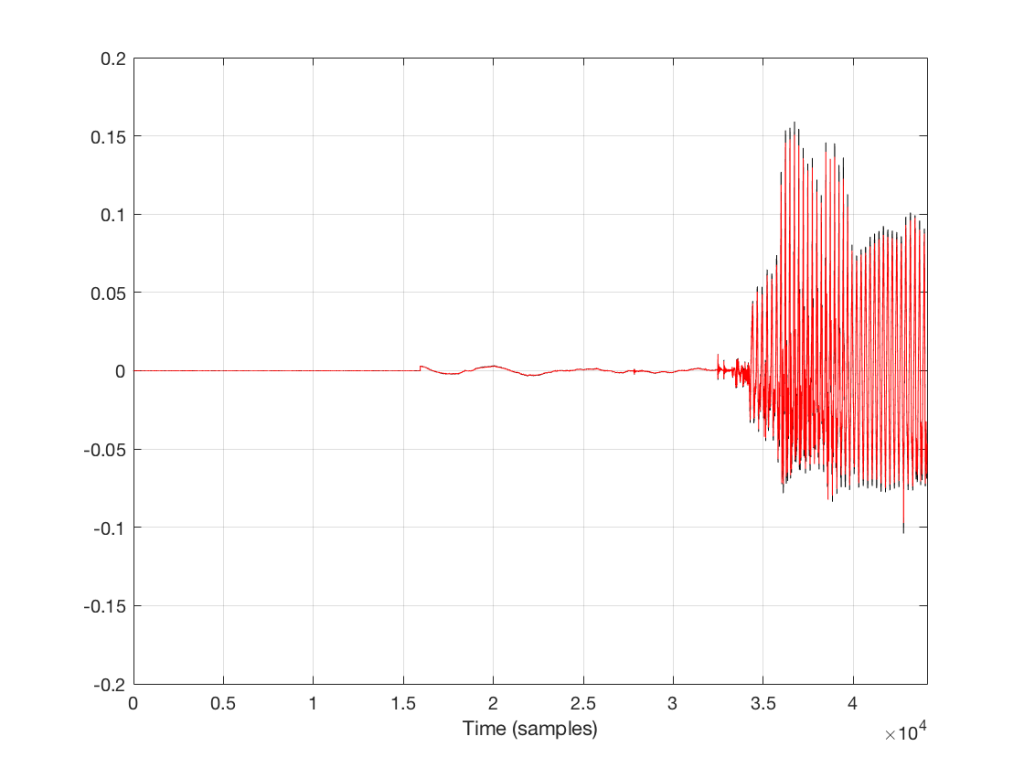
The plot above shows the first 44100 samples in the track (the first second of sound). The red plot is the decoded 128 kbps MP3. The black plot (which is difficult to see because it is overlapped by the red plot – except in the signal peaks) is the original file. For example, if I zoom into the area around the beginning of the sound (say, starting around sample number 15800) then we see this
So, as you can see in the two plots above, the decoded 128 kbps MP3 and the original 44.1/16 file are different. But, the difference is small relative to the levels of the signals themselves. The question is, how small is the difference, exactly?
We can find this out by subtracting the original signal from the decoded MP3 output, sample by sample. The result of this is shown in the plot below.
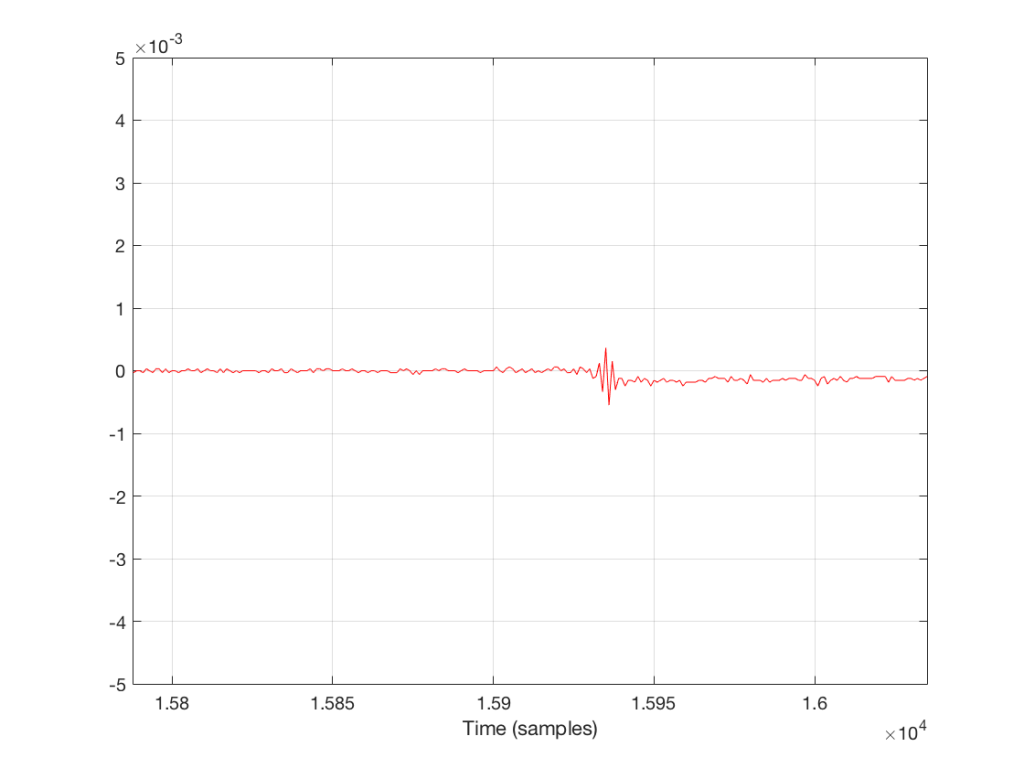
Notice that the vertical scale of the plot in Figure 3 is small. This is because it shows the difference between the two lines in Figure 2, which is also quite small.
Let’s think for a minute about how I arrived at the signal in Figure 3. I subtracted the Original signal from the MP3 output. In other words:
MP3 output – Original = Difference
If we consider that the difference between the MP3 output and the Original can be thought of as an “error”, and if I move the terms in the equation above, I get the following:
MP3 output – Original = Error
Original + Error = MP3 output
So, the question is: how loud is that error relative to the signal we’re listening to? The idea here is that, the louder the error, the easier it will be to detect.
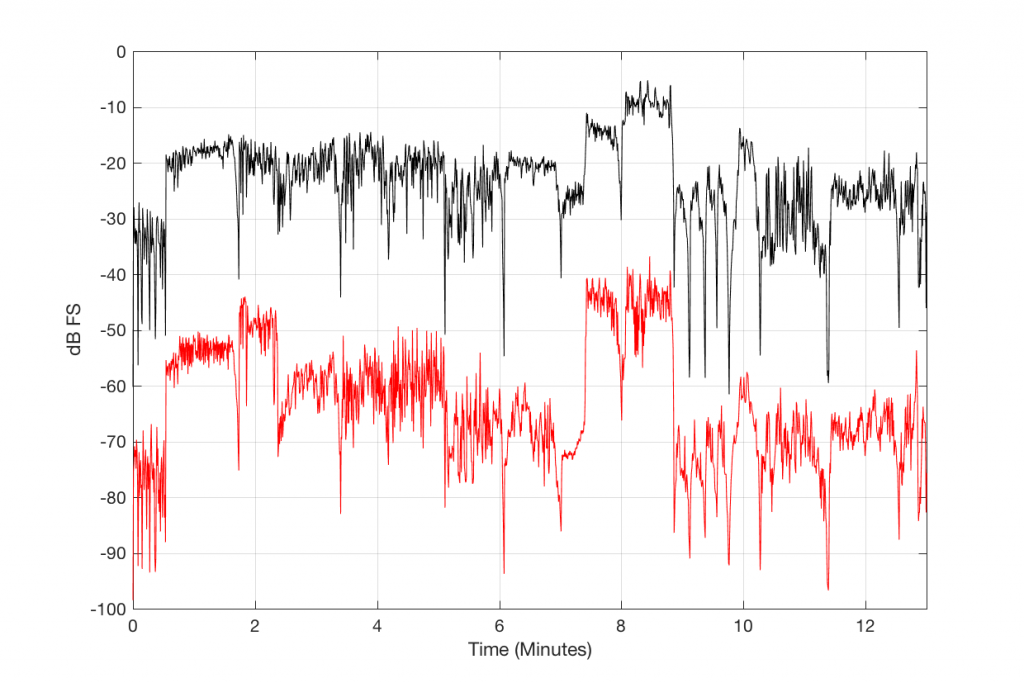
Figure 4, below, shows this level difference over time. The black curve is a running RMS level of the decoded 128 kbps MP3 file. As you can see there, it ranges from about -30 dB FS to about +10 dB FS. You may think that it’s strange that it “only” goes to -10 dB FS – but this is because the time window I’m using to calculate the RMS value of the signal is 500 ms long. The peaks of the track reach full scale, but since my time window is long, this tends to pull down the apparent level (because the peaks are short). (NB: If you want to argue about the choice of a 500 ms time window, please wait until I’ve followed up this posting with another one that divides things up by frequency band…)
The res curve in Figure 4 is a running RMS value of the Error signal – the difference between the MP3 file and the original. As you can see there, that error signal ranges from about -50 dB FS to about -30 dB FS, give or take…
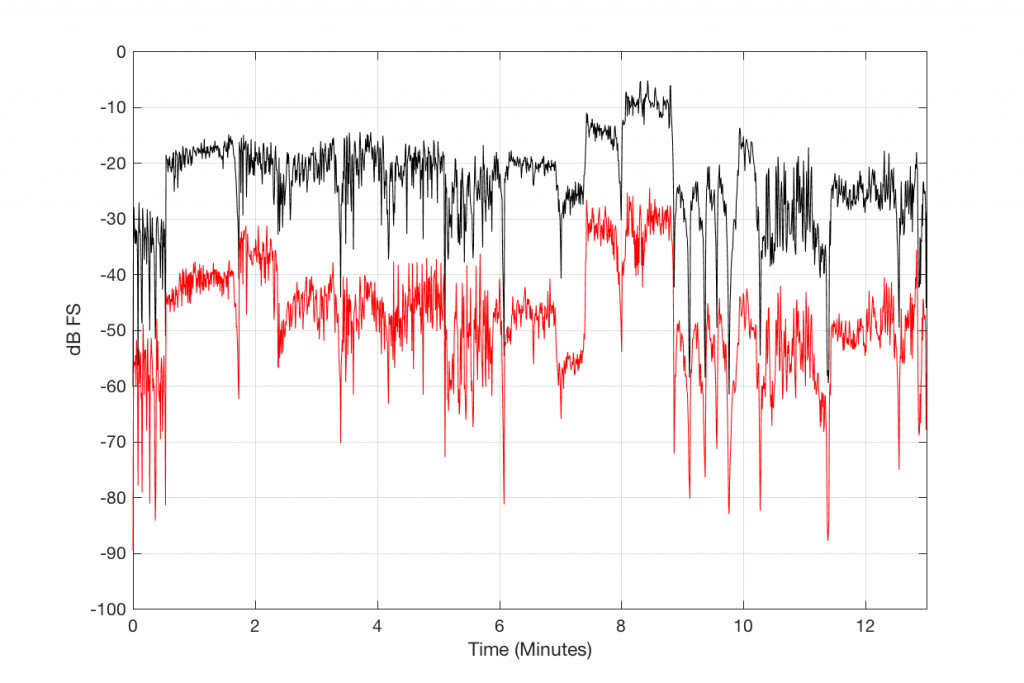
We can find the running value of the difference between the level of the MP3 file and the level of the Error it contains by subtracting the black curve from the red curve. The result of this is shown in Figure 5, below.
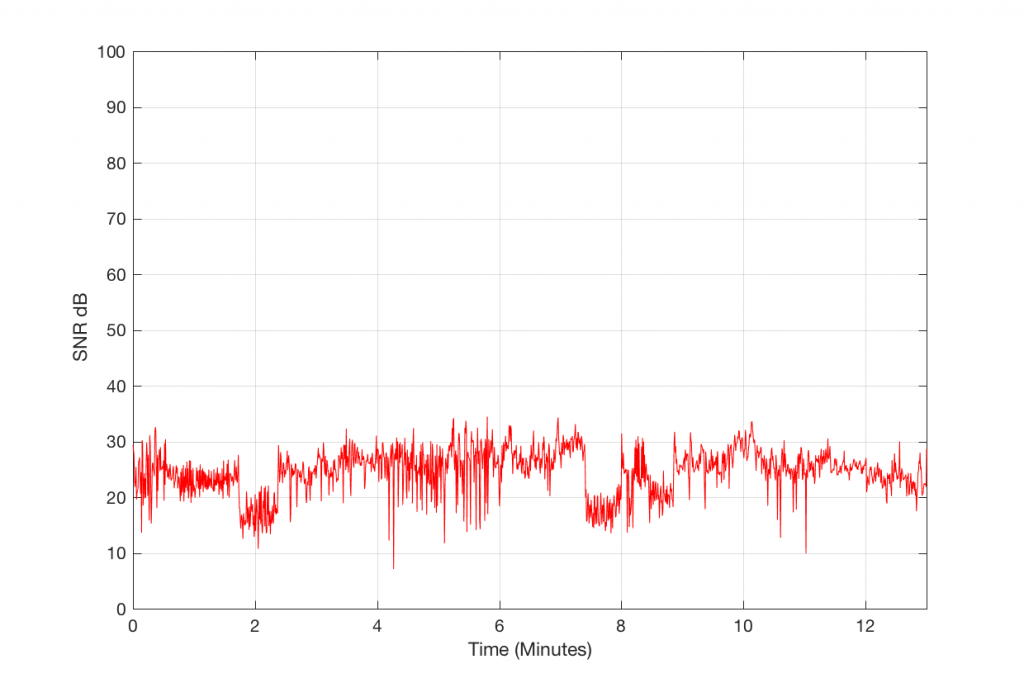
So, Figure 5, therefore, shows the measure of how loud the signal is relative to the error that makes it different from the original. If this error signal were just harmonic distortion, then we could call this a measure of THD in dB. If it were just good-old-fashioned noise, like on a magnetic tape, then we could call it a signal-to-noise ratio. However, this is neither distortion or noise in the traditional sense – or, maybe more accurately, it’s both…
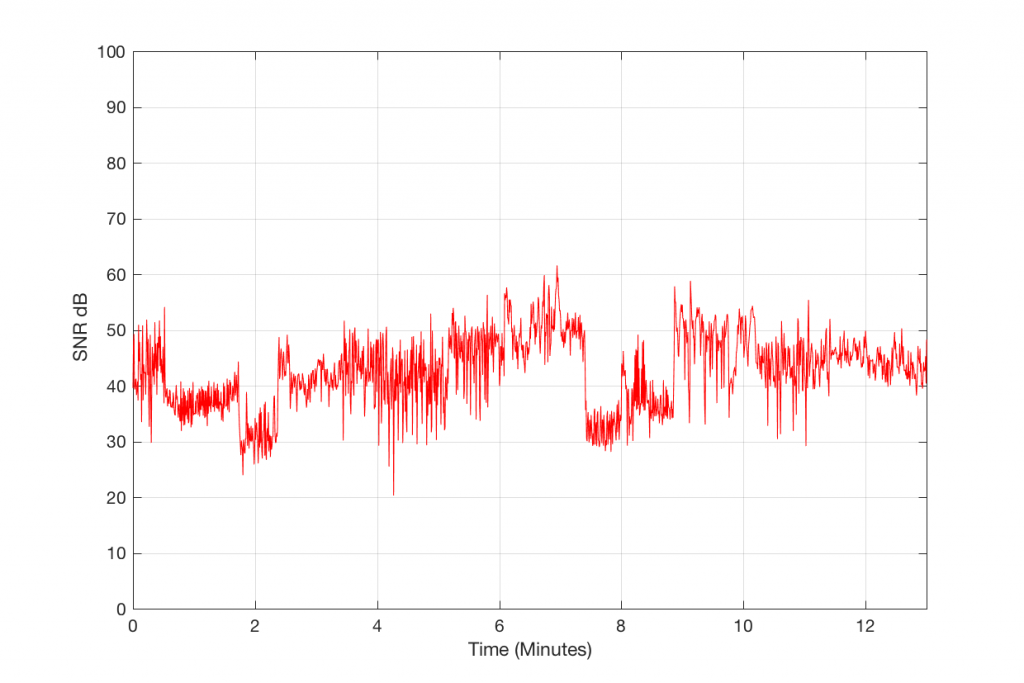
So, let’s call the plot in Figure 5 a “signal-to-error ratio”. What we can see there is that, for this particular track, for the settings that I used to make the 128 kbps MP3 file, the error – the MP3 artefacts – are only 20 to 25 dB below the signal most of the time. Now, don’t jump to conclusions here. This does not mean that they would be as audible as white noise that is only 25 dB below the signal. This is because part of the “magic” of the MP3 encoder is that it tries to ensure that the error can “hide” under the signal by placing the error signal in the same frequency band(s) as the signal. Typically, white noise is in a different band than the signal, so it’s easier to hear because it’s not masked. So, be very careful about interpreting this plot. This is a measurable signal-to-error ratio, but it cannot be directly compared to a signal-to-noise ratio.
Let’s now increase the bitrate of the MP3 encoding, allowing the encoder to increase the quality.
Figure 6 and 7 show the same information as before, but for a 256 kpbs encoding of the same track. As you can see there, by doubling the bitrate of the MP3, we have increased our signal-to-error ratio by about 10 to 15 dB or so – to about 35 or 40 dB.
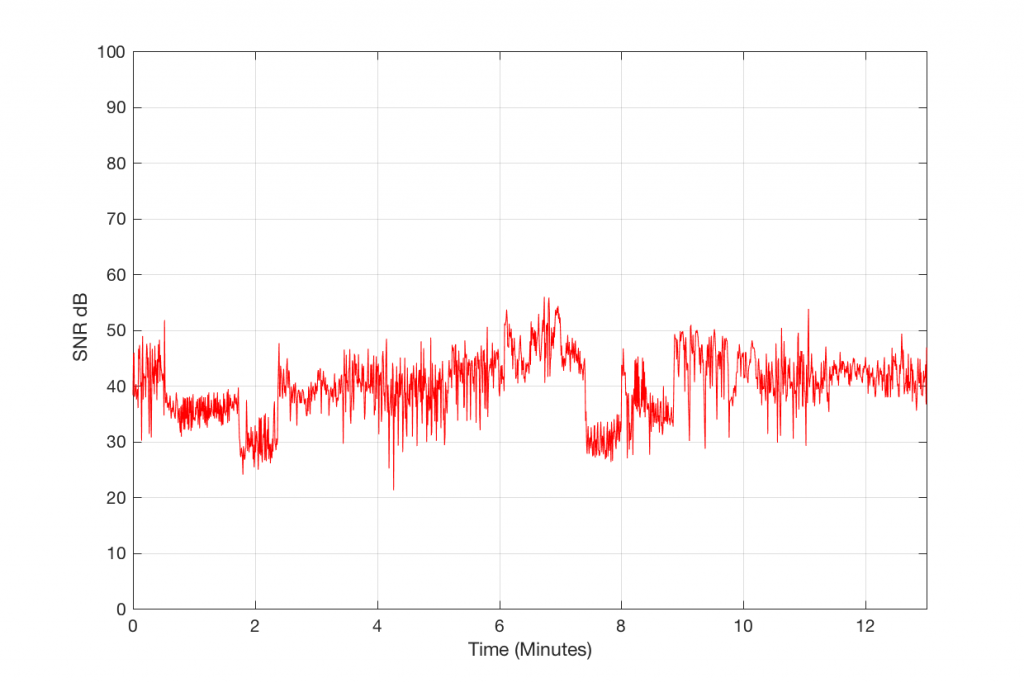
As you can see in Figures 8 and 9 above, increasing the MP3 bitrate to 320 kbps can improve the Signal-to-Error ratio from about 25 dB (for 128 kbps) to about 40 dB or so.
Now, if you’re looking carefully, you might notice that, some times in the track that I used for testing, the signal-to-error ratio is actually worse for the 320 kbps file than it is for the 256 kbps file – all other things being equal in the LAME converter parameters. This is a bit misleading, since what you cannot see there is the frequency spectrum of the error signal. I’ll deal with that in a future posting – with some more analysis and explanation to go with it.
For now, let’s play with the VBR presets in LAME. I’ll just show the signal-to-error plots for the 4 settings.
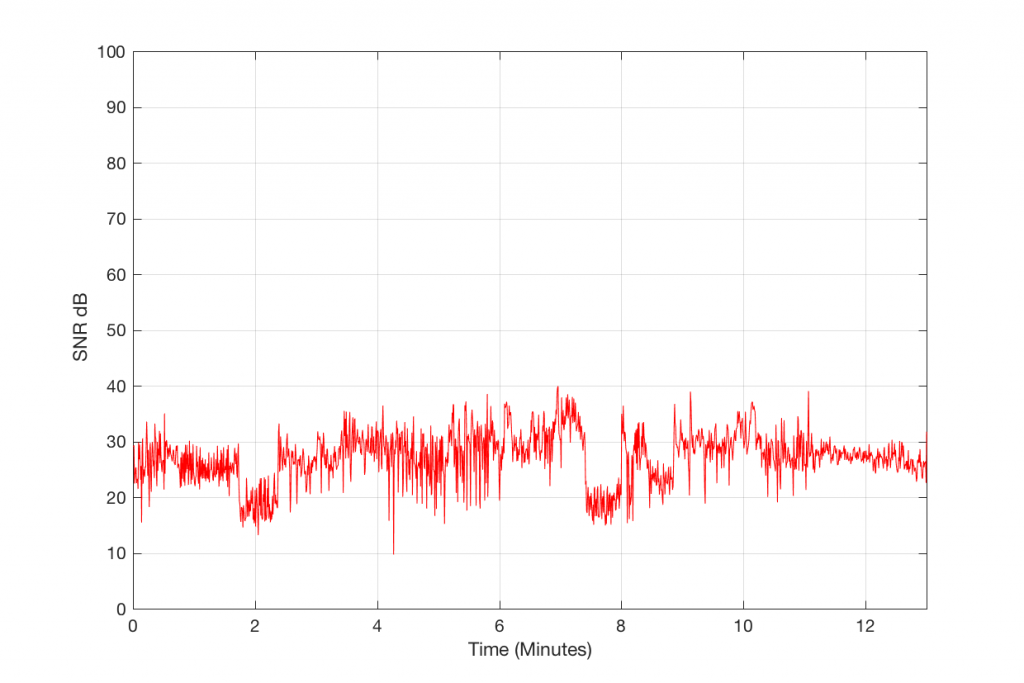
So, as you can see in Figures 10 through 13, the signal-to-error ratio can be improved with the VBR presets, reaching a peak of over 60 dB for the “Insane” setting, for this track…
As I said a couple of times above:
- You have to be careful about interpreting these graphs from a background of “knowing” what a SNR is… This error is not normal “distortion” or “noise” – at least from a perceptual point of view…
- I’ll go further with this, including some frequency-dependent information in a future posting.
Appendix – LAME parameters and verbose output
For the geeks…
MAC60090:mp3_demos ggm$ lame -b 320 -q 0 –verbose compilation_original.wav lame_320.mp3
LAME 3.99.5 64bits (http://lame.sf.net)
Using polyphase lowpass filter, transition band: 20094 Hz – 20627 Hz
Encoding compilation_original.wav to lame_320.mp3
Encoding as 44.1 kHz j-stereo MPEG-1 Layer III (4.4x) 320 kbps qval=0
misc:
scaling: 1
ch0 (left) scaling: 1
ch1 (right) scaling: 1
huffman search: best (outside loop)
experimental Y=0
…
stream format:
MPEG-1 Layer 3
2 channel – joint stereo
padding: off
constant bitrate – CBR
using LAME Tag
…
psychoacoustic:
using short blocks: channel coupled
subblock gain: 1
adjust masking: -10 dB
adjust masking short: -11 dB
quantization comparison: 9
^ comparison short blocks: 9
noise shaping: 1
^ amplification: 2
^ stopping: 1
ATH: using
^ type: 4
^ shape: 0 (only for type 4)
^ level adjustement: -12 dB
^ adjust type: 3
^ adjust sensitivity power: 1.000000
experimental psy tunings by Naoki Shibata
adjust masking bass=-0.5 dB, alto=-0.25 dB, treble=-0.025 dB, sfb21=0.5 dB
using temporal masking effect: yes
interchannel masking ratio: 0
…
Frame | CPU time/estim | REAL time/estim | play/CPU | ETA
37028/37028 (100%)| 2:07/ 2:07| 2:08/ 2:08| 7.5929x| 0:00
————————————————————————————————–
kbps LR MS % long switch short %
320.0 73.7 26.3 93.4 3.4 3.1
Writing LAME Tag…done
ReplayGain: -2.6dB
MAC60090:mp3_demos ggm$ lame -b 256 -q 0 –verbose compilation_original.wav lame_256.mp3
LAME 3.99.5 64bits (http://lame.sf.net)
Using polyphase lowpass filter, transition band: 19383 Hz – 19916 Hz
Encoding compilation_original.wav to lame_256.mp3
Encoding as 44.1 kHz j-stereo MPEG-1 Layer III (5.5x) 256 kbps qval=0
misc:
scaling: 1
ch0 (left) scaling: 1
ch1 (right) scaling: 1
huffman search: best (outside loop)
experimental Y=0
…
stream format:
MPEG-1 Layer 3
2 channel – joint stereo
padding: off
constant bitrate – CBR
using LAME Tag
…
psychoacoustic:
using short blocks: channel coupled
subblock gain: 1
adjust masking: -8 dB
adjust masking short: -8.8 dB
quantization comparison: 9
^ comparison short blocks: 9
noise shaping: 1
^ amplification: 2
^ stopping: 1
ATH: using
^ type: 4
^ shape: 1 (only for type 4)
^ level adjustement: -10 dB
^ adjust type: 3
^ adjust sensitivity power: 1.000000
experimental psy tunings by Naoki Shibata
adjust masking bass=-0.5 dB, alto=-0.25 dB, treble=-0.025 dB, sfb21=0.5 dB
using temporal masking effect: yes
interchannel masking ratio: 0
…
Frame | CPU time/estim | REAL time/estim | play/CPU | ETA
37028/37028 (100%)| 1:50/ 1:50| 1:51/ 1:51| 8.7235x| 0:00
————————————————————————————————–
kbps LR MS % long switch short %
256.0 71.6 28.4 93.4 3.4 3.1
Writing LAME Tag…done
ReplayGain: -2.6dB
MAC60090:mp3_demos ggm$ lame -b 128 -q 0 –verbose compilation_original.wav lame_128.mp3
LAME 3.99.5 64bits (http://lame.sf.net)
Using polyphase lowpass filter, transition band: 16538 Hz – 17071 Hz
Encoding compilation_original.wav to lame_128.mp3
Encoding as 44.1 kHz j-stereo MPEG-1 Layer III (11x) 128 kbps qval=0
misc:
scaling: 0.95
ch0 (left) scaling: 1
ch1 (right) scaling: 1
huffman search: best (outside loop)
experimental Y=0
…
stream format:
MPEG-1 Layer 3
2 channel – joint stereo
padding: off
constant bitrate – CBR
using LAME Tag
…
psychoacoustic:
using short blocks: channel coupled
subblock gain: 1
adjust masking: 0 dB
adjust masking short: 0 dB
quantization comparison: 9
^ comparison short blocks: 9
noise shaping: 2
^ amplification: 2
^ stopping: 1
ATH: using
^ type: 4
^ shape: 4 (only for type 4)
^ level adjustement: -3 dB
^ adjust type: 3
^ adjust sensitivity power: 1.000000
experimental psy tunings by Naoki Shibata
adjust masking bass=-0.5 dB, alto=-0.25 dB, treble=-0.025 dB, sfb21=0.5 dB
using temporal masking effect: yes
interchannel masking ratio: 0.0002
…
Frame | CPU time/estim | REAL time/estim | play/CPU | ETA
37028/37028 (100%)| 1:33/ 1:33| 1:34/ 1:34| 10.305x| 0:00
————————————————————————————————–
kbps LR MS % long switch short %
128.0 25.2 74.8 95.2 2.6 2.2
Writing LAME Tag…done
ReplayGain: -2.2dB
MAC60090:mp3_demos ggm$ lame –preset medium –verbose compilation_original.wav lame_medium.mp3
LAME 3.99.5 64bits (http://lame.sf.net)
Using polyphase lowpass filter, transition band: 17249 Hz – 17782 Hz
Encoding compilation_original.wav to lame_medium.mp3
Encoding as 44.1 kHz j-stereo MPEG-1 Layer III VBR(q=4)
misc:
scaling: 1
ch0 (left) scaling: 1
ch1 (right) scaling: 1
huffman search: best (outside loop)
experimental Y=1
…
stream format:
MPEG-1 Layer 3
2 channel – joint stereo
padding: all
variable bitrate – VBR mtrh (default)
using LAME Tag
…
psychoacoustic:
using short blocks: channel coupled
subblock gain: 1
adjust masking: 0 dB
adjust masking short: 0 dB
quantization comparison: 9
^ comparison short blocks: 9
noise shaping: 1
^ amplification: 2
^ stopping: 1
ATH: using
^ type: 5
^ shape: 2 (only for type 4)
^ level adjustement: -0 dB
^ adjust type: 3
^ adjust sensitivity power: 6.309574
experimental psy tunings by Naoki Shibata
adjust masking bass=-0.5 dB, alto=-0.25 dB, treble=-0.025 dB, sfb21=3.5 dB
using temporal masking effect: no
interchannel masking ratio: 0
…
Frame | CPU time/estim | REAL time/estim | play/CPU | ETA
37028/37028 (100%)| 0:18/ 0:18| 0:19/ 0:19| 53.116x| 0:00
32 [ 37] %
40 [ 4] *
48 [ 14] %
56 [ 8] %
64 [ 105] %
80 [ 423] %*
96 [ 831] %***
112 [ 2596] %%%********
128 [17134] %%%%%%%%%%%%%%%%%%%%***********************************************
160 [12811] %%%%%%%%%%%%%%%%%%%%%%%%***************************
192 [ 1330] %%****
224 [ 836] %%**
256 [ 683] %**
320 [ 216] %
——————————————————————————-
kbps LR MS % long switch short %
144.3 35.5 64.5 90.7 4.6 4.7
Writing LAME Tag…done
ReplayGain: -2.6dB
MAC60090:mp3_demos ggm$ lame –preset standard –verbose compilation_original.wav lame_standard.mp3
LAME 3.99.5 64bits (http://lame.sf.net)
Using polyphase lowpass filter, transition band: 18671 Hz – 19205 Hz
Encoding compilation_original.wav to lame_standard.mp3
Encoding as 44.1 kHz j-stereo MPEG-1 Layer III VBR(q=2)
misc:
scaling: 1
ch0 (left) scaling: 1
ch1 (right) scaling: 1
huffman search: best (outside loop)
experimental Y=0
…
stream format:
MPEG-1 Layer 3
2 channel – joint stereo
padding: all
variable bitrate – VBR mtrh (default)
using LAME Tag
…
psychoacoustic:
using short blocks: channel coupled
subblock gain: 1
adjust masking: -2.6 dB
adjust masking short: -2.6 dB
quantization comparison: 9
^ comparison short blocks: 9
noise shaping: 1
^ amplification: 2
^ stopping: 1
ATH: using
^ type: 5
^ shape: 2 (only for type 4)
^ level adjustement: -3.7 dB
^ adjust type: 3
^ adjust sensitivity power: 1.995262
experimental psy tunings by Naoki Shibata
adjust masking bass=-0.5 dB, alto=-0.25 dB, treble=-0.025 dB, sfb21=6.25 dB
using temporal masking effect: no
interchannel masking ratio: 0
…
Frame | CPU time/estim | REAL time/estim | play/CPU | ETA
37028/37028 (100%)| 0:19/ 0:19| 0:20/ 0:20| 48.732x| 0:00
32 [ 0]
40 [ 0]
48 [ 1] %
56 [ 0]
64 [ 15] %
80 [ 26] %
96 [ 17] %
112 [ 135] %
128 [ 1673] %*******
160 [15048] %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%*****************************
192 [15688] %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%*****************
224 [ 1986] %%%%%****
256 [ 1602] %%%%***
320 [ 837] %%**
——————————————————————————-
kbps LR MS % long switch short %
183.0 60.0 40.0 90.7 4.6 4.7
Writing LAME Tag…done
ReplayGain: -2.6dB
MAC60090:mp3_demos ggm$ lame –preset extreme –verbose compilation_original.wav lame_extreme.mp3
LAME 3.99.5 64bits (http://lame.sf.net)
polyphase lowpass filter disabled
Encoding compilation_original.wav to lame_extreme.mp3
Encoding as 44.1 kHz j-stereo MPEG-1 Layer III VBR(q=0)
misc:
scaling: 1
ch0 (left) scaling: 1
ch1 (right) scaling: 1
huffman search: best (outside loop)
experimental Y=0
…
stream format:
MPEG-1 Layer 3
2 channel – joint stereo
padding: all
variable bitrate – VBR mtrh (default)
using LAME Tag
…
psychoacoustic:
using short blocks: channel coupled
subblock gain: 1
adjust masking: -6.8 dB
adjust masking short: -6.8 dB
quantization comparison: 9
^ comparison short blocks: 9
noise shaping: 1
^ amplification: 2
^ stopping: 1
ATH: using
^ type: 5
^ shape: 1 (only for type 4)
^ level adjustement: -7.1 dB
^ adjust type: 3
^ adjust sensitivity power: 1.000000
experimental psy tunings by Naoki Shibata
adjust masking bass=-0.5 dB, alto=-0.25 dB, treble=-0.025 dB, sfb21=8.25 dB
using temporal masking effect: no
interchannel masking ratio: 0
…
Frame | CPU time/estim | REAL time/estim | play/CPU | ETA
37028/37028 (100%)| 0:21/ 0:21| 0:22/ 0:22| 44.584x| 0:00
32 [ 0]
40 [ 0]
48 [ 0]
56 [ 0]
64 [ 0]
80 [ 0]
96 [ 0]
112 [ 1] %
128 [ 0]
160 [ 408] %*
192 [ 1961] %%******
224 [16481] %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%***************
256 [13387] %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%*************
320 [ 4790] %%%%%%%%%%%%%*******
——————————————————————————-
kbps LR MS % long switch short %
245.6 70.9 29.1 90.7 4.6 4.7
Writing LAME Tag…done
ReplayGain: -2.6dB
MAC60090:mp3_demos ggm$ lame –preset insane –verbose compilation_original.wav lame_insane.mp3
LAME 3.99.5 64bits (http://lame.sf.net)
Using polyphase lowpass filter, transition band: 20094 Hz – 20627 Hz
Encoding compilation_original.wav to lame_insane.mp3
Encoding as 44.1 kHz j-stereo MPEG-1 Layer III (4.4x) 320 kbps qval=3
misc:
scaling: 1
ch0 (left) scaling: 1
ch1 (right) scaling: 1
huffman search: best (outside loop)
experimental Y=0
…
stream format:
MPEG-1 Layer 3
2 channel – joint stereo
padding: off
constant bitrate – CBR
using LAME Tag
…
psychoacoustic:
using short blocks: channel coupled
subblock gain: 1
adjust masking: -10 dB
adjust masking short: -11 dB
quantization comparison: 9
^ comparison short blocks: 9
noise shaping: 1
^ amplification: 1
^ stopping: 1
ATH: using
^ type: 4
^ shape: 0 (only for type 4)
^ level adjustement: -12 dB
^ adjust type: 3
^ adjust sensitivity power: 1.000000
experimental psy tunings by Naoki Shibata
adjust masking bass=-0.5 dB, alto=-0.25 dB, treble=-0.025 dB, sfb21=0.5 dB
using temporal masking effect: yes
interchannel masking ratio: 0
…
Frame | CPU time/estim | REAL time/estim | play/CPU | ETA
37028/37028 (100%)| 0:28/ 0:28| 0:28/ 0:28| 33.937x| 0:00
——————————————————————————-
kbps LR MS % long switch short %
320.0 73.7 26.3 93.4 3.4 3.1
Writing LAME Tag…done
ReplayGain: -2.6dB
Modern acoustical design
Czech Vinyl
Early portable audio device
A small list of high-end Internet radio stations
Tuning requires precision and accuracy
B&O Tech: “Auto” loudness
#76 in a series of articles about the technology behind Bang & Olufsen loudspeakers
If you look at the comments section to a posting I wrote about ABL, you’ll see a short conversation there between me and a happy Beomaster 8000 customer who said that I had made an error in making sweeping generalisations about the function of a “loudness” filter in older gear. I said that, in older gear, a loudness filter boosted the bass (and maybe the treble) with a fixed gain, regardless of listening level (also known as “the position of the volume knob”). Henning said that this was incorrect, and that, in his Beomaster 8000, the amount of boost applied by the loudness filter was, indeed, varied with volume.
So, I dusted off one of our Beomaster 8000’s (made in the early 1980’s) to find out if he was correct.
I sent an MLS signal to the Tape 1 input (left channel) of the Beomaster 8000, and connected a differential probe to the speaker output. (The reason for the probe was to bring the signal back down to something like a line level to keep my sound card happy…)
I set the volume to 0.1, switched the loudness filter off, and measured the magnitude response.
Then I turned the loudness filter on, and measured again.
I repeated this for volume steps 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, 4.5, 5.0, and 5.5. I didn’t do volume step 6.0 because this overloaded the input of my sound card and created the weird artefacts that occur when you clip an MLS signal. No matter…
Then I plotted the results, which are shown below.
Remember that these are NOT the absolute magnitude response curves of the Beomaster 8000. These are the DIFFERENCE between the Loudness ON and Loudness OFF at different volume settings.
At the top, you see a green line which is very, very flat. This means that, at the highest volume setting I tested (vol = 5.5) there was no difference between loudness on and off.
As you start coming down, you can see that the bass is boosted more and more, starting even at volume step 5.0 (the purple line, second from the top). At the bottom volume step (0.1, there is a nearly 35 dB boost at 20 Hz when the loudness filter is on.
You may also notice two other things in these plots. The first is the ripple in the lower curves. the second is the apparent treble boost at the bottom setting. Both of these artefacts are not actually in the signal. These are artefacts of the measurements that I did. So, you should ignore them, since they’re not there in “real life”.
So, Henning, I was wrong and you are correct – the Beomaster 8000 does indeed have a loudness filter that varies with volume. I stand corrected. Thanks for the info – and a fun afternoon!