Let’s say that we have to do an audio measurement of a Device Under Test (DUT) that has one input and one output, as shown below.

We don’t know anything about the DUT.
One of the first things we do in the audio world is to measure what most people call the “frequency response” but is more correctly called the “magnitude response”. (It would only be the “frequency response” if you’re also looking at the phase information.)
The standard way to do this is to use an impulse response measurement. This is a method that relies on the fact that an infinitely short, infinitely loud click contains all frequencies at equal magnitude. (Of course, in the real world, it cannot be infinitely short, and if it were infinitely loud, you would have a Big Bang on your hands… literally…)
If we measure the DUT with a single-sample impulse with a value of 1, and use an FFT to convert the impulse response to a frequency-domain magnitude response and we see this:

… then we might conclude that the DUT is as perfect as it can be, within the parameters of a digital audio system. The click comes out just like it went in, therefore the output is identical to the input.
If we measure a different DUT (we’ll call it DUT #2) and we see this:

… then we might conclude that DUT #2 is also perfect. It’s just an attenuator that drops the level by half (or -6.02 dB).
However, we’d be wrong.
I made both of those DUTs myself, and I can tell you that one of those two conclusions is definitely incorrect – but it illustrates the point I’m heading towards.
If I take DUT #1 and send in a sine tone at about 1 kHz and look at the output, I’ll see this:

As you can see there, the output is a sine wave. It looks like one on the top plot, and the bottom plot tells me that there ONLY signal at 1 kHz, which proves it.
If I send the same sine tone through DUT #2 and look at the output, I’ll see this:
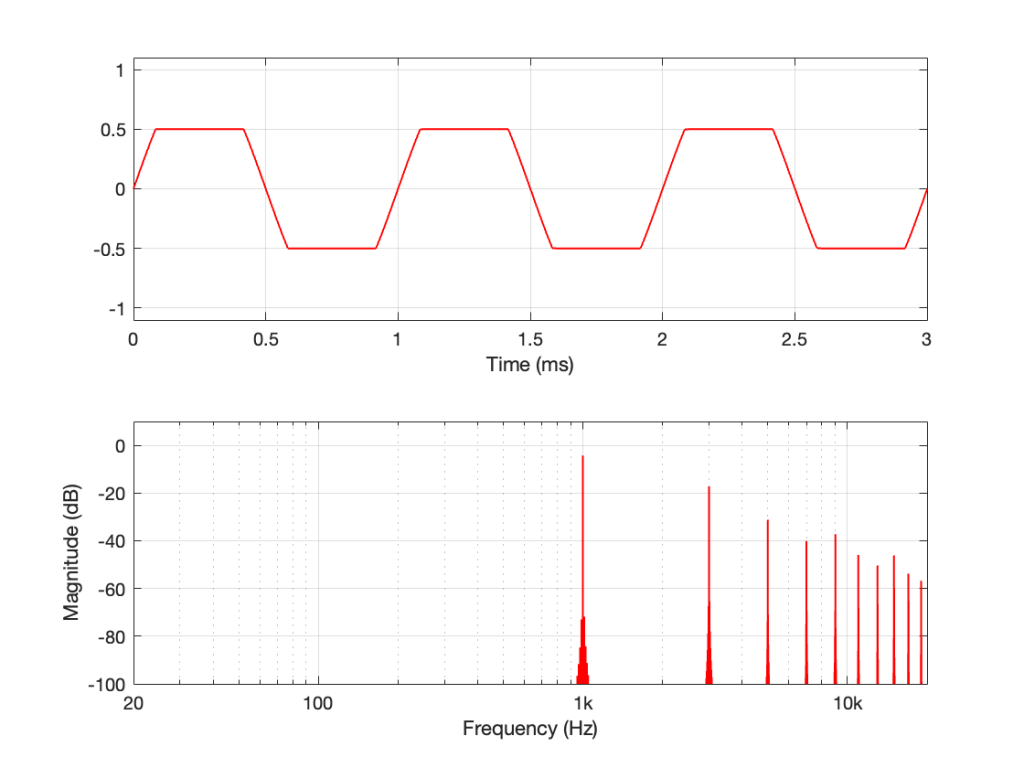
As you can see there, DUT #2 clips the input signal so that it cannot exceed ±0.5. This turns the sine wave into the beginnings of a square wave, and generates lots of harmonics that can be seen in the lower half of the plot.
What’s the point?
The point is something that is well-known by people who make audio measurements, but is too easily forgotten:
An Impulse Response measurement only shows you the linear behaviour of an audio device. If the system is non-linear, then your impulse response won’t help you. In a worst case, you’ll think that you measured the system, you’ll think that it’s behaving, and it’s not – because you need to do other measurements to find out more.
The question is “what is ‘non-linear’ behaviour in an audio device?”
This is anything that causes the device to make it impossible to know what the input was by looking at the output. Anything that distorts the signal because of clipping is a simple example (because you don’t know what happened in the input signal when the output is clipped). But other things are also non-linear. For example, dynamic processors like compressors, limiters, expanders and noise gates are all non-linear devices. Modulating delays (like in a chorus or phaser effect), or a transmission system with a drifting clock are other examples. So are psychoaoustic lossy codecs like MP3 and AAC because the signal that gets preserved by the codec changes in time with the signal’s content. Even a “loudness” function can be considered to have a kind of non-linear behaviour (since you get a different filter at different settings of the volume control).
It’s also important to keep in mind that any convolution-based processing is using the impulse response as the filter that is applied to the signal. So, if you have a convolution-based effects unit, it cannot simulate the distortion caused by vacuum tubes using ONLY convolution. This doesn’t mean that there isn’t something else in the processor that’s simulating the distortion. It just means that the distortion cannot be simulated by the convolver.*
P.S.
The reason for the title: “One measurement is worse than no measurements” is that, when you do a measurement (like the impulse response measurement on DUT #2) you gain some certainty about how the device is behaving. In many cases, that single measurement can tell the truth, but only a portion of it – and the remainder of the (hidden) truth might be REALLY bad… So, your one measurement makes you THINK that you’re safe, but you’re really not… It’s not the measurement that’s bad. The problem is the certainty that results in having done it.
* Actually, one of the questions on my comprehensive exams for my Ph.D. was about compressors, with a specific sub-question asking me to explain why you can’t build a digital compressor based on convolution (which was a new-and-sexy way to do processing back then…). The simple answer is that you can’t use a linear time-invariant processor to do non-linear, time-variant processing. It would be like trying to carry water in a net: it’s simply the wrong tool for the job.