#40 in a series of articles about the technology behind Bang & Olufsen loudspeakers

 

Once-upon-a-time, I wrote a posting explaining why a loudspeaker’s biggest enemy is your listening room. The basic problem is as follows:

• when you listen to a loudspeaker in a room, roughly 99% or more of what you hear is sound that goes outwards from the loudspeaker, fills up the room, bounces around and then gets to you. Only about 1% or less of what you hear actually comes directly to you from the loudspeaker…
• rooms have early reflections that mess up the tone colour and the imaging of the loudspeakers
• rooms have room modes that make the bass response extremely uneven, and very different from place to place in the room
• rooms have reverberation that, generally, makes some frequency bands sound louder because they last longer in time

So, to borrow a phrase from South Park’s Mr. Mackey, “rooms are bad, m’kay?

For this posting, we’re going to focus only on the third issue there: that of “room modes” and a couple of ways to deal with them. To begin with, let’s talk about what a room mode is.

The short version

The PowerPoint-single-slide-of-bullet-points version of an explanation of room compensation is as follows:

• A room mode is a resonant frequency where the room “sings along” with the sound of the loudspeaker, making that pitch (or note) sound louder than others.
• This resonance can be measured using a microphone
• To reduce the effect of this problem, the loudspeaker can either
  • reduce the amount of energy it emits at that particular frequency
  • actively absorb energy at that frequency
• This means that one detrimental aspect of the room’s acoustical behaviour on the sound of the loudspeaker will be reduced

 

That’s it. However, of course, the real story is a little more nuanced (or maybe just more complicated) than that. So, if you’re interested in knowing a little more, read on!

 

 

Resonance

If you put a kid on a swing and push him (not too hard… we don’t want anyone to get hurt here…) and stand back, you’ll watch him swing back and forth, decreasing a little in distance from the resting position each time, until eventually, he’ll come to a stop. Now, do it again, and pay attention to his movement. He moves forwards, away from the resting position until he reaches a high point, then stops, comes backwards past the resting position to a high point, stops, and then moves forwards again. We’ll call that total return trip from going forwards at the resting position to being back again, going forwards at the resting position, one cycle. The number of times the kid does this for each period of time (let’s say, in this case, each minute) is called the frequency – how frequently he’s repeating the motion. The maximum distance he moves from the resting position (to the highest point in the cycle) is called the amplitude.

Now, if you pay really close attention to the movement of the kid on the swing, you might notice that, even though the amplitude of the cycle decreases over time, the frequency doesn’t change.

Another example of this kind of motion is shown in the video in this posting. However, that video is not for the faint-of-heart. Watch it at your own risk…

Okay, if you watched that video and you’re still awake, let’s move on.

There are a couple of important concepts to glean from this discussion so far.

• If you have a system that can resonate (like a spring and a mass, or a kid on a swing), it will “want to” resonate at a fundamental frequency.
• You can trigger that system to resonate at its fundamental frequency by injecting energy into the system (like lifting the mass, or pushing the kid)

Another example of a system that “wants” to resonate is a string that’s fixed on both ends – like a guitar string. It has a fundamental frequency that is determined by the string’s mass and tension. The cool thing about a string is that it also resonates at multiples of that fundamental frequency (better known as harmonics or overtones – which almost mean the same thing, but not quite – but the difference is irrelevant here). So, if you have a guitar string that’s tuned to 100 Hz (an abbreviation for “Hertz” which is the word we use to mean “cycles per second”) then it will also resonate at harmonics with frequencies of 200 Hz, 300 Hz, 400 Hz, and so on. If you inject energy into the string (by plucking it with your finger, for example), then the string’s total vibration will include resonances at all those frequencies, on up to ∞ Hz (in theory… not in practice…). You’ll have a resonance at each individual harmonic, each with its own amplitude (how much the string is vibrating or moving away from its resting position – the higher the amplitude, the louder it is) and the total sum of all of these results in the shape (and sound) of the string.

To see this in action, check out this video.

At this point, you’re probably wondering “what does this have to do with my room?” We’re getting there… I promise.

One last example of a system that resonates is the air in a pipe (like an organ pipe, for example). If you could shrink yourself down to the size of a molecule and get inside an organ pipe, you’d see that you’re looking down a long tube that’s capped at both ends (we won’t talk about the other kind of pipe that’s open on one end… let’s pretend those don’t exist…). If you face one end of the pipe and push the air molecule next to you towards it, it will push the one in front of it, which will push the one in front of it, and so on, until the shoving match ends at the cap at the end of the pipe. (See this page for a good animation of the story so far…) That last molecule can’t push the “wall” so it bounces back, which winds up in a return shoving match (or pressure wave…) that will eventually push against you, and you’ll push the molecule behind you, which keeps repeating until the wavefront gets to the cap at the opposite end of the pipe, which reflects, and sends wavefront back to you again.

Now, what happens if, while all of that is happening, you are pushing repeatedly? Every time the wave bounces back at you, you push it again in the same direction that the particles want to move in (this is exactly the same as pushing a kid on a swing at exactly the right time to make him swing higher and higher – you time the push so that he’s moving in the same direction as you’re pushing).

Take a look at the top part of the animation below.

Let’s say that you’re the red molecule and you’re in a pipe. You push and pull the two adjacent particles (one in front, one behind) exactly in sync with the wave that’s reflecting off the two ends of the pipe, and you’re helping to inject energy into the fundamental resonance of the air column inside the pipe. The result is something called a “standing wave”. it’s called this because it looks like the wave is “standing still” and just changing in instantaneous amplitude over time, but the reality is that this is just an illusion. What is actually happening is that the right-going wave is aligned with the left-going wave to perfectly cancel each other out at all times in the middle of the pipe, and to result in big changes in pressure at the ends of the pipe. Check out the third animation on this page for a good explanation of this summing or “superposition” of waves resulting in a standing wave.

Just like a string, a pipe will also resonate at harmonics of the fundamental, in multiples of the frequency of the lowest resonance. So, if the pipe resonates at 150 Hz, then you will also have resonances at 300 Hz, 450 Hz, and so on… I’ll show some animations with examples of these later in the posting.

Room Modes

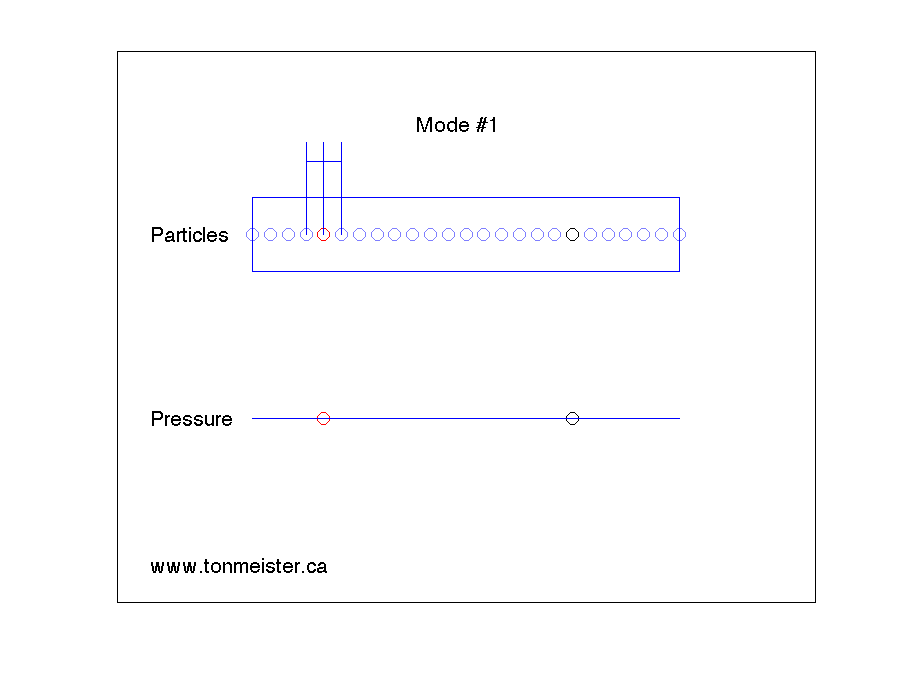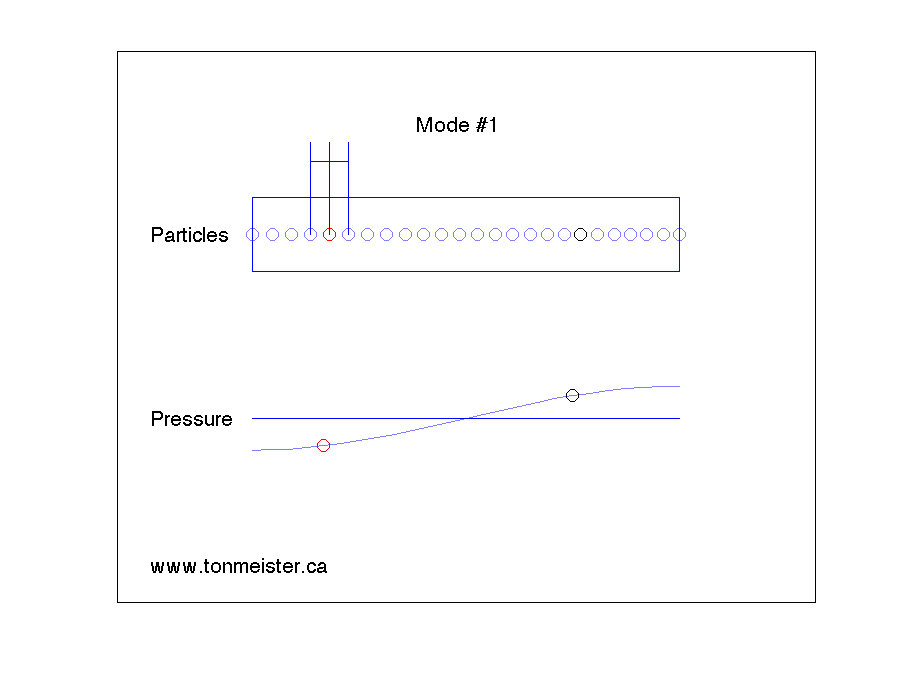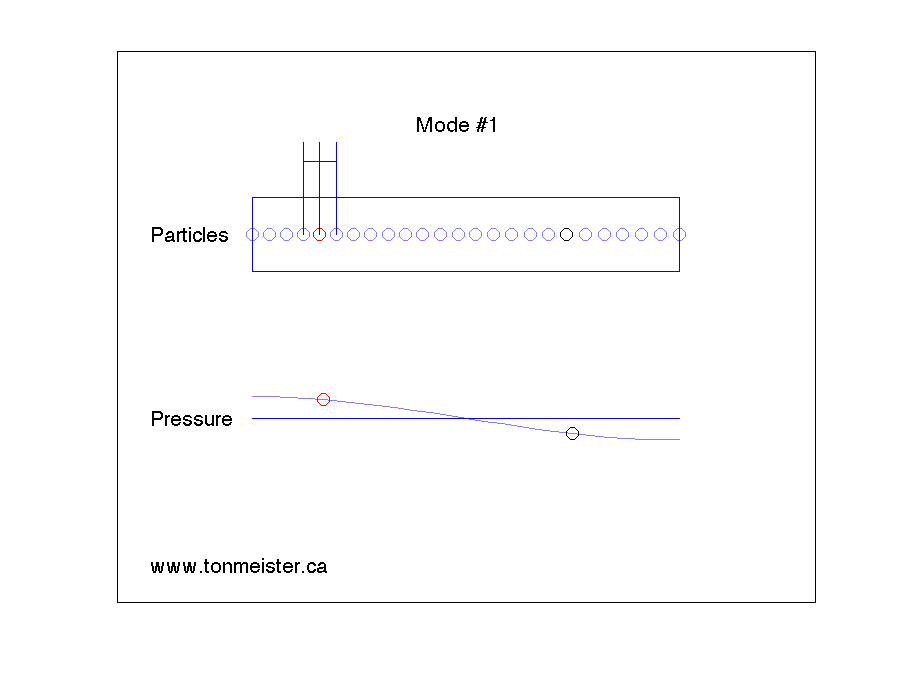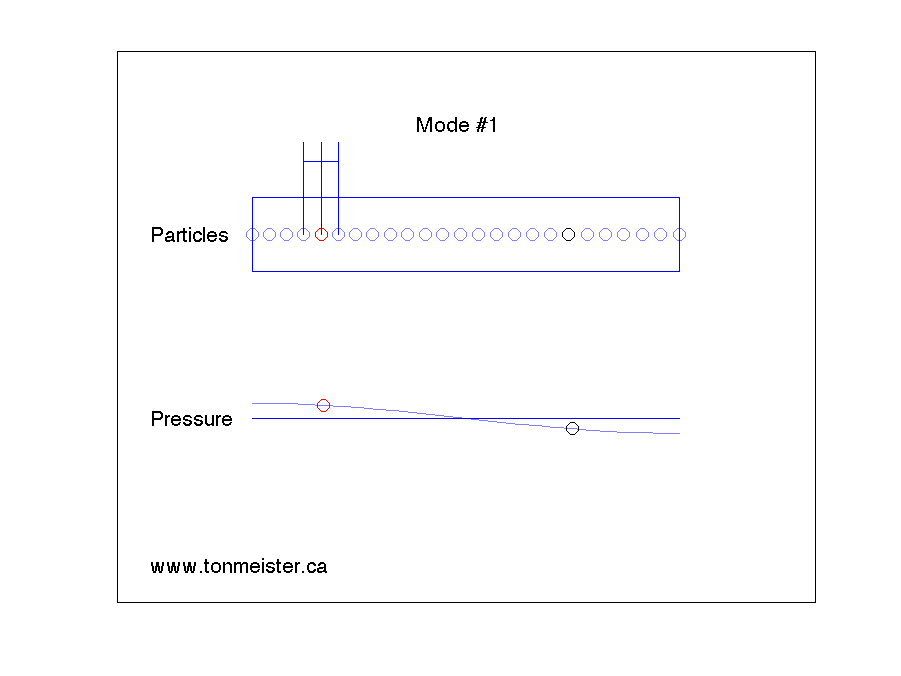
The nice thing (at least it’s nice in that it helps our understanding – it’s not actually nice in real life…) is that a room behaves just like a very big, very wide, organ pipe. So, for example, when I sit in a listening room that is 5 m wide by 6 m long, some of the resonances that I hear “singing along” with every sound source in the room are exactly the same frequencies as the ones that would come out of organ pipes 5 m long and 6 m long.

Take a look at that animation above once again. You can think of the red dot as the loudspeaker, pushing and pulling the adjacent air particles in time. You sit at the listening position at the black dot – the adjacent air particles push and pull your eardrum in and out of your head. The pressure of the sound wave (the only thing we’re going to worry about in this posting) can be thought of as a measure of how close two adjacent air particles are (shown by the three vertical lines in the top part, and represented by the entire bottom part of the animation).

So, as the loudspeaker woofer (for example) moves in and out of the enclosure on a kick drum hit, it injects energy into the room at many different frequencies. If the frequency of the resonance in the room is one of the frequencies in the woofer’s signal, then that note will sound much louder than the other notes, making for a very uneven bass. This is because the room “wants” to resonate (or “sing along”) at that particular frequency, so a little energy coming into it will give a large result (just like a series of small, but well-timed, pushes of a kid on a swing can build up over time to result in the kid moving back and forth much more than you’re pushing).

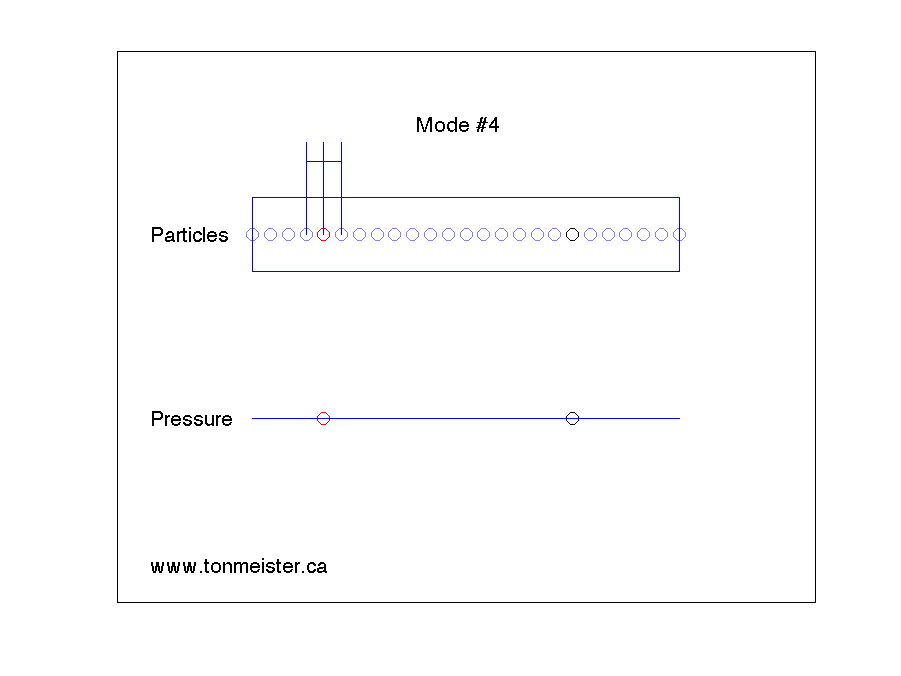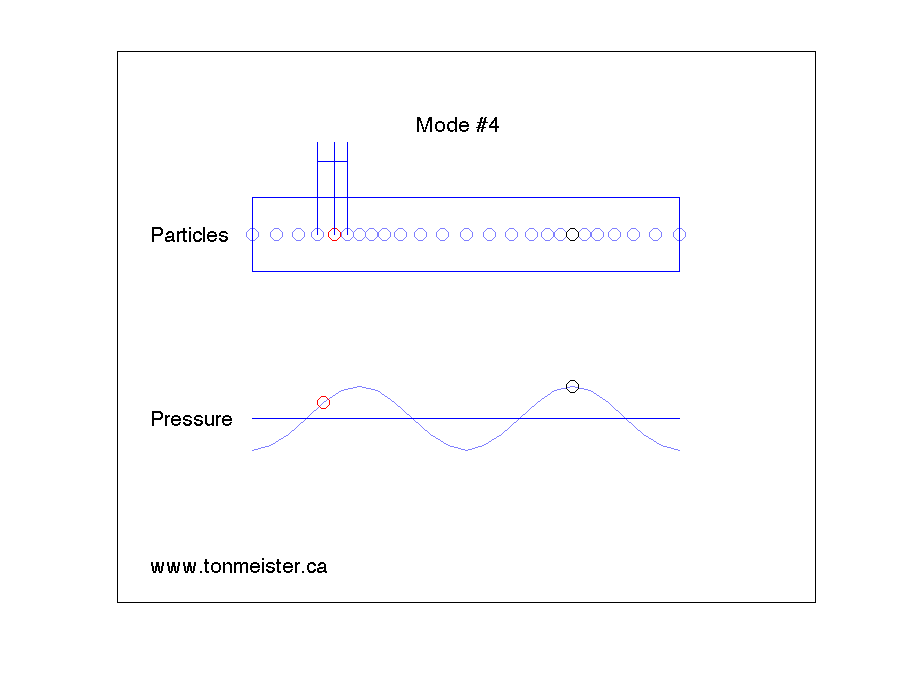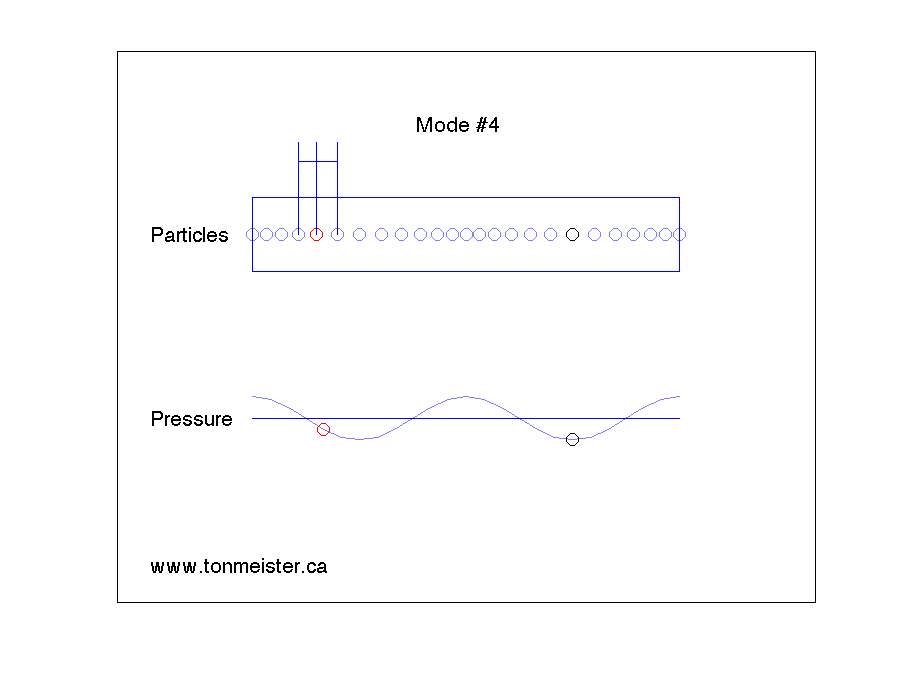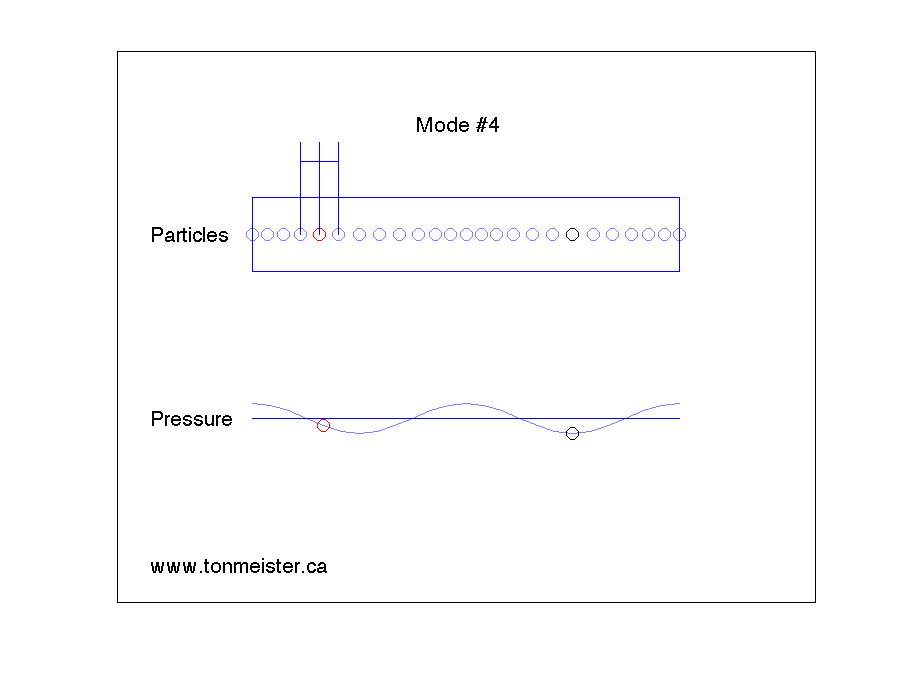
This will happen not only at the fundamental frequency of the resonance, but its harmonics. The second harmonic is shown below.

The third harmonic looks like the animation below.

And the fourth harmonic looks like the animation below.

We won’t go any higher than this.

There are some things to notice in these animations.

1. The air particles at the walls on either end of the room experience the maximum pressure change. This is because one of the particles cannot push the wall, so it receives the full effect of the pressure.
2. There are places in the room where the pressure does not change over time. For example, in the case of Mode #1 in the first animation, the point at the exact middle of the room doesn’t have a change in pressure. This doesn’t mean that the air particles are not moving – they are. However, the ones in the middle of the room are staying the same distance from each other – so the pressure doesn’t change over time.

If you are sitting at a point in the room where there is no change in pressure caused by the mode (say, for example, you’re the black dot in Mode #2, above), then you will not be able to hear the room mode. It’s still happening around you – but at your exact position, since there is no change in pressure over time, it doesn’t exist. However, this doesn’t mean that you won’t hear anything at that particular frequency – you will – it’s just that the sound you hear (from the loudspeaker) doesn’t have the room mode singing along with it at your location.

Similarly, if the loudspeaker is placed at a location where there is no change in pressure when the room mode is ringing (for example, the location of the red circle in Mode #3), then the loudspeaker will not trigger this mode to ring. Energy will come out of the loudspeaker at that frequency, and you’ll be able to hear it – but the room mode will not “sing along” with the signal, since the loudspeaker can’t inject energy into it. (Note that this is statement is based on at least two assumptions: (1) that the loudspeaker is a pressure source, and (2) that it is infinitely small. At least one of these assumptions is incorrect.)

This means that, looking at the four animations above, and assuming that the red dot is the loudspeaker and the black dot is the listener:

• We need to fix Mode #1, since the loudspeaker and the listener are “coupled” to it (meaning that they are not sitting on a point where there is no pressure change in the mode).
• We do not need to fix Mode #2 since, although the loudspeaker is triggering the mode to ring, the listener cannot hear it. (However, if the loudspeaker was placed somewhere else, this mode could be a problem.)
• We do not need to fix Mode #3 since the loudspeaker cannot trigger the mode, so no one hears it (although the mode will occur for other sound sources in the room).  (Also, if the listening position was placed somewhere else, this mode could be a problem.)
• We need to fix Mode #4.

How can we fix this?

As I said in the PowerPoint version above, we have two basic strategies for dealing with room modes.

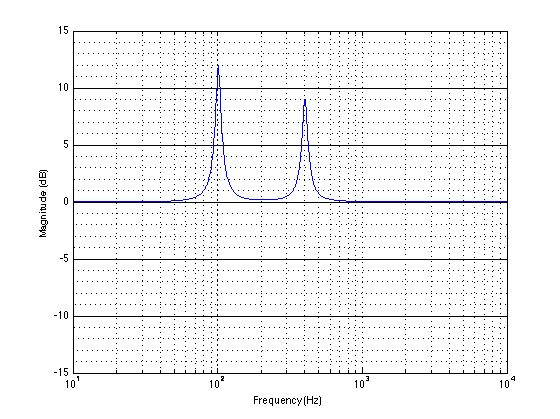
The first is a “symptom attenuation” approach: the room mode makes some frequencies louder than others, so we’ll just reduce the level of those frequencies by the same amount. If the room boosts 100 Hz by 6 dB, then we’ll put a dip of -6 dB at 100 Hz in the signal sent to the loudspeaker. This doesn’t actually correct the problem – it just covers it up. It’s a bit like taking a pain killer because you’ve broken your leg. You are no longer in pain, but the problem still exists… The trick here is to measure the response of the loudspeaker at the listening position (this is easy) and find out which frequencies appear to be boosted by the room. We then make an equalisation which is that same response turned “upside down” so a peak in the measured response becomes a dip in the loudspeaker’s processing.

As I said, this covers up the problem but it doesn’t solve it. The thing to remember is that a room mode appears to be louder because the room moves the energy in time. For example, if you pluck a guitar string, you “activate it” for a very short period of time. The resonance of the string takes that energy and extends it in time so you hear a note that goes on for seconds after the pluck. A room mode does the same thing – it “rings” in time, smearing the energy coming out of your loudspeakers (say, a kick drum hit) and extending it like a guitar string ringing. If you send less energy out of the loudspeaker at the same frequency of the room mode, then the total result at the listening position will be quieter, but it’s still ringing in time. (So, instead of plucking the guitar string and then stopping it, we’re just plucking with less force.)

The second method is a little more complicated, but works better. Since we have control of the loudspeaker, what we can do is to send the sound we want out of it – but we’ll add an extra signal that cancels the room mode by working against it. If we go back to the original description where we were a little air particle in a pipe, we send the signal out, and when it comes back, reflected off the cap, we’ll send a signal out of the loudspeaker that “sucks it back in”. This way, the loudspeaker acts as an active absorber. (This is a little like the way a person on a trampoline can stop jumping by using his/her legs to absorb the push-back from the springs. See this video at 0:53, for example.)

The great thing is that, if you’re smart and a little lucky, both of these approaches are the same thing. If we consider the room mode to have the same characteristics as a “minimum phase” peaking filter (which, in isolation, it does), then, if we can measure it correctly, we can implement its exact reciprocal. This means that the magnitude response of the filter we insert into the loudspeaker’s processing will be the exact opposite of the room’s response. In addition to this, the phase response of the filter is, at any frequency, opposite in polarity to the phase response of the room mode (in isolation). This means that both approaches are rolled into one solution.

 

 

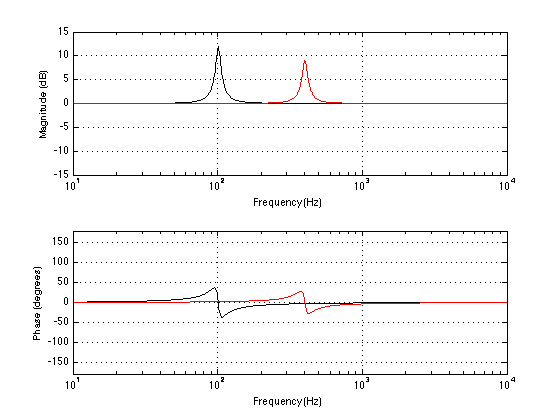
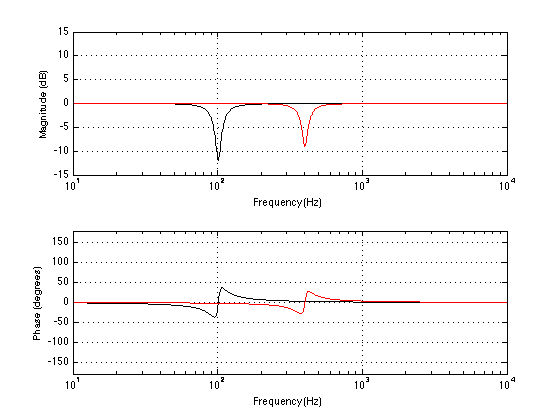
Of course, this is very theoretical. However, in practice the concept holds true enough that it results in a noticeable improvement in the sound of a loudspeaker in the listening position, assuming that you are careful about the measurements you make around that position. If you choose to make a room correction filter that applies to the whole room, and not just one listening position, then you should measure the room in many different and varied locations. This will give you a “general” compensation that is better, on average, for everyone in the room – although it might make one specific location (like, say, the sweet spot) worse. If, instead, you just measure one location by placing the microphone in a tight area around the sweet spot, for example, then the compensation filter will be optimised for that location, but it will probably make the rest of the room worse as a result.

Active Room Compensation gives you this option to customise the room compensation filters as they best suit your needs. If you’re the kind of person with one chair and no friends, then you measure around that chair and you never leave it while you’re listening. If you’re the kind of person who has lots of friends, or who moves around while you listen, then you create a compensation filter that fixes the entire room, on average.

Of course, in a perfect world, you would be able to make both of these measurements in advance and save each one as a preset – then you would be able to select the one that best suits the situation when the time arises… Or, you could combine them and build a filter that corrects the room, with emphasis on the sweet spot…

P.S. As I mentioned briefly in this posting, Active Room Compensation has one additional feature – multichannel processing. That will be explained later in Part 2.