So, you want to build a loudspeaker…

One of the questions you’ll probably be asking yourself is whether you want to build a ported loudspeaker (sometimes called a “bass reflex” loudspeaker) or one with a sealed enclosure. If you want to know the general reasons why most people think that you should choose one or the other, go somewhere else for information – or maybe come back here later (maybe I’ll talk about it in a later posting).

For this posting, I want to look at a couple of things that I haven’t seen elsewhere – mostly because it helps me to understand the difference between ported and sealed loudspeaker enclosures a little better.

Let’s take a loudspeaker driver and put it in a box. For the purposes of this discussion, we’ll simulate a 10″ driver with mostly-real Thiele-Small parameters in a simulated sealed box. The box has a volume, but we’ll leave out any possible internal modes to keep things simple for now. We’ll also ignore additional effects such as diffraction – we’re just looking at the how the enclosure’s volume and the port dimensions affect the response of the system.

If we sweep a sine wave into the driver, keeping the voltage constant, and we measure the sound pressure level in front of the driver, we’ll see that the total system (the loudspeaker in a sealed box) acts as a minimum phase, second-order high pass filter. Therefore it has a rising slope of 12 dB/octave in the low end. The Q of that high-pass filter will be dependent on the relationship of the driver’s parameters and the size of the box.

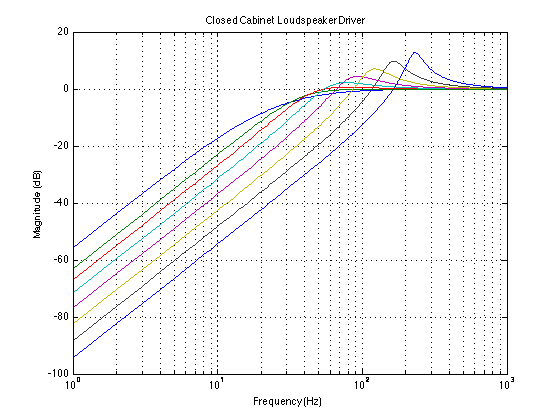
In the plots above, you can see the results on the magnitude response of changing the enclosure volume. The blue curve on the far left is the response you’d get from putting the driver in an infinite baffle (actually, I simulated an enclosure of about a cubic kilometre or so… So not quite infinite, but pretty big for a woofer cabinet…). Notice that it has the highest output at the lowest frequency, but you don’t get as much output around the knee as you do with the other curves. As the enclosure volume is made smaller (The green curve is 1000 litres, and each curve after that, moving left to right, is for a volume of one-half the previous one, so, 500 l, 250 l, 125 l, 62.5 l, 31.25 l, and 15.625 l. Remember – the driver that we’re simulating here isn’t real, so don’t worry about the actual volumes – we’re just worried about the differences in magnitude response as the volumes get smaller.)

You can see in the plots that, by making the volume behind the driver smaller, we do a couple of things at the same time.

1. One is that, the smaller the enclosure, the higher the cutoff frequency of the resulting high pass filter. This is because the “spring” supplied by the air in the enclosure gets stiffer (or less compliant) as the box gets smaller, so it rings at a higher frequency.
2. Secondly, you’ll notice that the Q of the high pass filter increases as the enclosure gets smaller. This is because the damping factor of the total system (which is, in turn inversely related to the Q – the lower the damping, the higher the Q) decreases as the spring gets stiffer ( and the compliance goes down), if neither the mass nor the losses in the system change.

Both of these are basically the same as having a series RLC circuit and decreasing the capacitor value. The resonant frequency will go up, and the damping factor will go down.

Now, what happens if we wanted to build a ported loudspeaker instead? For now, let’s just use the same loudspeaker driver, a 1000 litre enclosure and we’ll add a port. We’re keeping it simple, so we will just add the port as a pipe sitting outside the enclosure so it doesn’t take away from the enclosure’s volume. Also we will not include the port’s volume as part of the enclosure volume. Also, because this isn’t the real world, we’ll make the port’s output in the same physical location as the loudspeaker driver to avoid any problems with propagation delay and interference at the microphone location.

The above plots show the result of this imaginary ported box with different port lengths, keeping all other parameters constant. I’ve made the losses in the port low so that the port has a bigger contribution to the total magnitude response, and therefore is easier to see. Remember – we’re not simulating the real world – we’re intentionally making the simulation produce curves that show patterns to better understand what’s going on. The ports that I’ve simulated are 10 cm in diameter, and have a length of (again from left-to-right) 1.6 m, 800 cm, 400 cm, 200 cm, 100 cm, 50 cm, 25 cm, and 12.5 cm.

What can we see in these plots?

1. Firstly, you can see that the slope of the high pass filter is now steeper than it was with the closed cabinet. This is because a ported loudspeaker enclosure results in a fourth-order high-pass system, so we have a slope of 24 dB/octave. This means that, in the very low end, we have a LOT less output from the ported system than the sealed system.
2. Secondly, you can see that, in this case, changing the port length has an puts a bump in the output’s magnitude response around a frequency that is dependent on the port length. The longer the port, the lower the centre frequency of the bump. This isn’t a surprise, since making the port longer lowers the resonant frequency of the Helmholtz resonator. In real life, the bump probably wouldn’t be as prominent – I made it obvious by simulating a port with very low losses (Those losses are the result of things like turbulence around the ends of the port and friction where the air “plug” in the port is rubbing against the sides of the port and the energy is converted to heat.)
3. Thirdly, you will see that the cutoff frequency of the system doesn’t change as much as it did when I was changing the volume of the sealed enclosure.

So, how do these systems compare? You’ll often hear people say “I chose to make a bass reflex loudspeaker so that I would get more bass out of the system.” The question is, does this sentence make sense? Is this really a good reason to choose a ported enclosure over a sealed one when you’re building a loudspeaker? Let’s look at what magical wonders adding a port had brought to our pretend loudspeaker…

The above plots show the difference in the output of the systems, showing the relative outputs of the ported systems (the colours are arranged to be the same as the ones in the previous plot so you know which port is which length) compared with the same enclosure without a port (in other words, the green curve from the top plot). Basically, all I’ve done here is subtracted the green curve from the top plot from all the curves in the second plot. If the result is 0 dB (as it is in the high frequency region for all of the curves, then this means that the two systems have the same output. If the value for a given frequency is positive, then this means that the ported system is louder than the sealed system. If the value is negative, then it means that the ported system is quieter by that amount.

As can be seen in that plot, there is a frequency region for all ported systems where you get more output for the same voltage. In the high end, both systems give the same output (because that’s so far above the port resonance that it’s basically not a part of the system, so they both behave the same way). In the low end, the ported system gives much less output because it’s a 4th-order high pass instead of a 2nd-order high pass like the sealed enclosure system.

So far, we can see that a ported system does appear to give you more bass for the same input voltage, assuming that you’ve tuned the port to give you more output in a band that you call bass – however, below that band, you get less. So you might be “robbing Peter to pay Paul” – which might not necessarily be a good idea.

Some people (who might know a little more about what they’re talking about than the last people I mentioned) say “I’m going to build a bass reflex loudspeaker instead of a sealed system to reduce distortion in the driver at the port resonance.” Now why on earth would they say that? Well, a little more digging (not much more digging, admittedly) will turn up an extra little piece of information: the driver moves less at frequencies around the port resonance. For example, at the resonant frequency of the port, the Helmholtz resonator acts against the driver, pushing it out when it tries to move in and pulling it in when it tries to move out. As a result, the excursion of the driver drops. In an extreme (non-real-world) case, if there are no losses in the port or the enclosure, then the driver’s excursion would be 0 at the port resonance. The greater the losses, the less this will be true.

So, let’s check out our two systems again, this time, looking at the driver excursion (peak excursion, to be precise) by frequency.

The above plot shows the peak excursion of the driver in the sealed cabinet. The colours correspond directly to the curves in the first plot at the top of the posting so that you can see the kind of magnitude response you get for the excursion. As you can see, in all cases, the excursion of the driver in the high frequency region is nearly 0 mm – the higher we get, the closer we get to 0 mm. You can also see that, in the low end, the excursion levels out. The more level the excursion plot, the closer the slope of the magnitude response is to a “perfect” 12 dB/octave. This is because the sounds pressure only comes from the air moved by the driver, and because the sound pressure level is proportional to the acceleration of the driver. As the frequency drops and the excursion stays the same, the acceleration drops by 12 dB per halving of frequency because it’s the derivative of the velocity which drops by 6 dB per halving of frequency, because it’s the derivative of the excursion in time.

Of course, if your driver can’t handle the excursions we see here (for example, the one I’m using for this simulation can only move 8 mm before it starts to get unhappy) then you might have something to worry about here. How you deal with that problem, however, is your problem.

So, what would the excursion look like for the same driver in a ported cabinet? Let’s have a look!

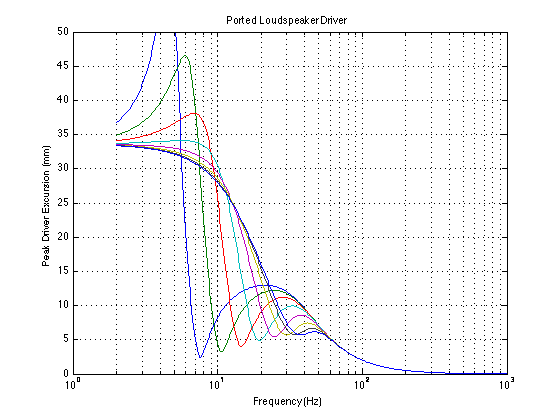
The plot shown above has the peak excursion curves for the same driver in the ported cabinet for the port lengths listed high above… As you can see, starting at the top end, the excursion of the driver is nearly 0 mm, just as in the case of the sealed cabinet. As the frequency drops, the excursion starts to increase. However, then something weird happens. Going lower in frequency, we can see that the driver excursion levels out and starts to drop, with a minimum value at the resonance of the port. If you’re very attentive, you’ll notice that this frequency isn’t exactly the same as the frequency of the bump in the total system’s magnitude response. That’s not a big surprise, since there is some other frequency (in this weird, non-real-life system) where the summed outputs of the driver and port give you more output than they do at the port resonance (actual results may vary). Anyway, going below the port resonance, you can see that the excursion of the driver really takes off and becomes much greater than it was with the sealed system. That’s because there’s nothing there to stop it. At frequencies that are much lower than the port resonance, the system behaves as if the driver wasn’t in a box at all, so it’s free to move as far as it wants to go. (remember that our non-real-life system isn’t limited by things like the maximum excursion of the suspension… The values in the plot show the excursion that the driver “wants” to hit – it’s just held back by real life.)

So, you may be asking yourself a question at this point: “Why is it that, at very low frequencies, the driver’s excursion is much higher in the ported system than in the sealed system, but you get less output?” Good question! The reason is that, at frequencies far below port resonance, you get almost as much output from the port as the driver. The only problem is that the port is just delivering the pressure at the back of the driver to the outside world. So, when the front of the driver goes positive, the back of the driver (and therefore the port) goes negative, and the two cancel each other at the listening position. Putting the port opening at the back of the loudspeaker won’t help much. It will just make the propagation distance a little longer, therefore a little later, but they’ll still cancel each other. This is why the total output of the ported system drops faster as you go lower in frequency – the lower you go, the more the driver and the port cancel each other. They’re both working really hard (and therefore, so is your amplifier), but you get next-to-nothing.

However, let’s back up a bit. There is that issue of the lower driver excursion around the port resonance. This is true. So, if you have a loudspeaker driver that doesn’t like excursion (maybe, say, it distorts when it moves to far) in a particular frequency band, then maybe a port could alleviate the problem. However, beware of frequencies below! Danger danger! (In other words, you might want to put a high pass filter in your system to keep things running smoothly below the port resonance…)

A couple of plots ago, we did some subtraction to compare the magnitude responses of the ported systems to a sealed system. Let’s do the same for the excursion plots. The above figure shows the difference between the peak excursion of the driver in the ported systems, and that of the driver in a sealed enclosure of the same volume. Negative values mean that the ported cabinet driver moves less than the sealed cabinet one. Positive values mean that the ported cabinet driver moves further than the sealed cabinet one.

As you can see in those curves, in the high frequencies, the driver will have the same excursion in both cases. Secondly, there is some region in all cases where the driver moves less in a ported system than in a sealed cabinet of the same volume. At low frequencies, the ported cabinet driver moves further than the sealed cabinet equivalent (yet has less total output, remember!). An interesting detail to note here is to look carefully at this plot with the magnitude difference plot. For example, take a look at the left-most blue curve. The ported system driver has a lower (or equal) excursion than the sealed system driver from about 6.5 Hz and up. Looking at the magnitude response difference curve for the same system, we can see that we get about 6 or 7 dB more output from the ported system at 6.5 Hz, with less and less benefit as we go higher in frequency. Below 6.5 Hz, although we get more output from the ported system for about an octave, it comes at the cost of a much greater excursion, which would probably not be good for our driver.

So what?

Okay, let’s be honest here. I’ve made two very simulated systems, and only changed one variable in each system to see what happens. And, I can absolutely guarantee that (1) no loudspeaker driver in the world has the parameters of the one I’ve simulated and (2) if you built the system I’ve simulated, it wouldn’t behave as I’ve shown here. This is a very isolated, idealised simulation, intentionally designed to make the changes I was making obvious. However, the issues that I’ve made obvious are basically true – I’ve just done a little exaggeration…

What’s the moral of the story? Well, I’m not really sure of all of them. One moral is certainly “sticking a port on a loudspeaker enclosure is not a free ticket to more bass”. Another moral is “people who use ports to reduce driver excursion might not know what they’re talking about”. Probably the most important moral is “don’t trust everything you read” – even the stuff you read here.

Post Script

If you REALLY want to learn this stuff correctly, go read the following:

Closed Box Loudspeaker Systems – Part 1: Analysis

Closed Box Loudspeaker Systems – Part 2: Synthesis

Vented Box Loudspeaker Systems – Part 1: Small Signal Analysis

Vented Box Loudspeaker Systems – Part 2: Large Signal Analysis

Vented Box Loudspeaker Systems – Part 3: Synthesis

Vented Box Loudspeaker Systems – Part 4: Appendices

When you’re done with those, please explain them to me.